标签:模拟 down break div 注意 problem opera alt 一个
Problem 1 双色球(ball.cpp/c/pas)
【题目描述】
机房来了新一届的学弟学妹,邪恶的chenzeyu97发现一位学弟与他同名,于是他当起了善良的学长233
“来来来,学弟,我考你道水题检验一下你的水平……”
一个栈内初始有n个红色和蓝色的小球,请你按照以下规则进行操作
以上3步骤为一次操作
如栈中都是红色球,则操作停止,请问几次操作后停止
chenzeyu97出完题发现他自己不能AC所以想请你帮忙
【输入格式】
第一行为一个整数n,表示栈的容量为n
第二行为一个字符串,第i个字符表示自顶向下的第i个球的颜色,R代表红色,B代表蓝色
【输出格式】
一个整数表示操作数
【样例输入】
样例1:
3
RBR
样例2:
4
RBBR
【样例输出】
样例1:2
样例2:6
【样例解释】
样例1:
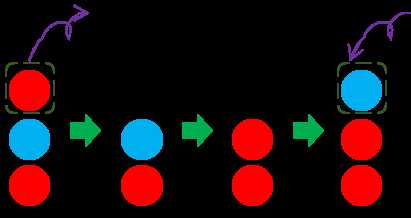
样例2:
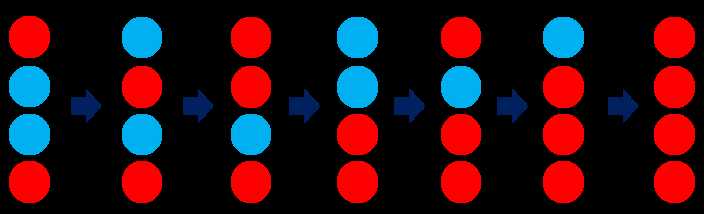
【数据范围】
50%的数据,1<=n<=20
100%的数据,1<=n<=50
Problem 2 魔方(cube.cpp/c/pas)
【题目描述】
ccy(ndsf)觉得手动复原魔方太慢了,所以他要借助计算机。
ccy(ndsf)家的魔方都是3*3*3的三阶魔方,大家应该都见过。

(3的“顺时针”改为“逆时针”,即3 4以图为准。)
ccy(ndfs)从网上搜了一篇攻略,并找人翻译成了他自己会做的方法。现在告诉你他的魔方情况,以及他从网上搜到的攻略,请你求出最后魔方变成什么样子。
【输入格式】
第一行,一串数字,表示从网上搜到的攻略。
下面6*3行,每行3个数字,每三行表示魔方一个面的情况,六个面的顺序是前、后、左、右、上、下。
【输出格式】
6*3行,表示处理后的魔方,形式同输入。
【样例输入】
23
121
221
111
123
321
111
123
321
132
132
231
132
121
112
233
332
111
333
【样例输出】
123
222
113
212
321
113
122
321
132
121
333
121
211
312
113
331
111
331
【样例解释】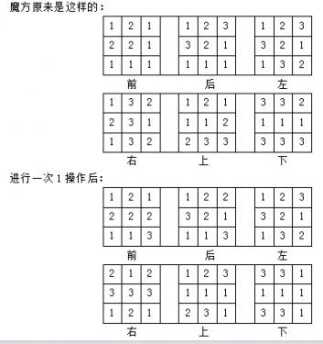
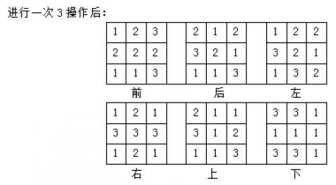
【数据范围】
40%的数据,攻略的长度小于5且仅有4种操作的其中一种
100%的数据,攻略的长度小于100
Problem 3 czy的后宫(harem.cpp/c/pas)
【题目描述】
czy要妥善安排他的后宫,他想在机房摆一群妹子,一共有n个位置排成一排,每个位置可以摆妹子也可以不摆妹子。有些类型妹子如果摆在相邻的位置(隔着一个空的位置不算相邻),就不好看了。假定每种妹子数量无限,求摆妹子的方案数。
【输入格式】
输入有m+1行,第一行有两个用空格隔开的正整数n、m,m表示妹子的种类数。接下来的m行,每行有m个字符1或0,若第i行第j列为1,则表示第i种妹子第j种妹子不能排在相邻的位置,输入保证对称。(提示:同一种妹子可能不能排在相邻位置)。
【输出格式】
输出只有一个整数,为方案数(这个数字可能很大,请输出方案数除以1000000007的余数。
【样例输入】
2 2
01
10
【样例输出】
7
【样例说明】
七种方案为(空,空)、(空,1)、(1、空)、(2、空)、(空、2)、(1,1)、(2,2)。
【数据范围】
20%的数据,1<n≤5,0<m≤10。
60%的数据,1<n≤200,0<m≤100。
100%的数据,1<n≤1000000000,0<m≤100。
注:此题时限1.5s是因为本评测机跑太慢,大家正常做
但写的太丑可能T一俩个点
Problem 4 mex(mex.cpp/c/pas)
【题目描述】

【输入格式】

【输出格式】
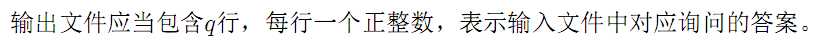
【样例输入】
7 5
0 2 1 0 1 3 2
1 3
2 3
1 4
3 6
2 7
【样例输出】
3
0
3
2
4
【样例解释与数据范围】

T1:
这题一开始看数据范围这么小,于是乎直接模拟,T5个点

1 #include<cstdio> 2 #include<cstdlib> 3 #include<algorithm> 4 #include<cstring> 5 #define MAXN 55 6 using namespace std; 7 int stack[MAXN],top=0; 8 int cnt; 9 int n; 10 int ans=0; 11 int main() 12 { 13 scanf("%d",&n); 14 // 1 red 2 blue; 15 for(int i=n;i>=1;i--){ 16 char c; 17 scanf(" %c",&c); 18 if(‘R‘==c){ 19 stack[i]=1; 20 cnt++; 21 } 22 else{ 23 stack[i]=2; 24 } 25 } 26 top=n; 27 while(1){ 28 ans++; 29 while(1==stack[top]&&top){ 30 top--; 31 cnt--; 32 } 33 if(2==stack[top]&&top){ 34 stack[top]=1; 35 cnt++; 36 } 37 for(int i=top+1;i<=n;i++){ 38 stack[i]=2; 39 } 40 top=n; 41 if(cnt==n){ 42 break; 43 } 44 } 45 printf("%d\n",ans); 46 return 0; 47 }
后来发现其实是找规律的:
对于一个栈,我们只考虑从栈顶到第一个blue,即RRRRB,因为所有操作不可能干到这个B底下,
我们姑且无视B下面的东西吧
然后发现操作1次为BBBBR,再次无视这个R,变成了BBBB
然后发现操作分别变成RBBB BRBB RRBB ……
如同0000 1000 0100 1100 ……
规律出来了,对于栈中自上向下第i个B,把它变成R需要2^(i-1),然后依次处理即可
注意:用long long的时候就不可以把int类型的i直接(1<<(i-1)),会炸的

1 #include<cstdio> 2 #include<cstdlib> 3 #include<algorithm> 4 #include<cstring> 5 #define ll long long 6 using namespace std; 7 int n; 8 ll ans; 9 ll Power(int p){ 10 ll ret=1; 11 for(int i=1;i<=p;i++){ 12 ret*=2; 13 } 14 return ret; 15 } 16 int main() 17 { 18 char c; 19 scanf("%d",&n); 20 for(int i=0;i<n;i++){ 21 scanf(" %c",&c); 22 if(‘B‘==c){ 23 ans+=Power(i); 24 } 25 } 26 printf("%lld\n",ans); 27 return 0; 28 }
T2:
暂且不提供题解
T3:
设f[i][j]表示i个座位,必须以第j个妹子为结尾的方案
然后f[i][j]=∑f[i-1][k] (j,k不矛盾)
当然矩阵快速幂优化即可,详见代码
注意:
1,妹子可以为空,那么直接m++即可,多出来的矩阵用1补足
2,输入的01矩阵和转移矩阵正好反的
3,对于矩阵较大的内存,最好不要用递归快速幂,直接用循环即可
4,切记要开long long!!!

1 #include<cstdio> 2 #include<cstdlib> 3 #include<algorithm> 4 #include<cstring> 5 #include<iostream> 6 #define MAXN 105 7 #define MOD 1000000007 8 #define ll long long 9 using namespace std; 10 struct Mat{ 11 int len; 12 ll s[MAXN][MAXN]; 13 Mat(){ 14 len=0; 15 memset(s,0,sizeof(s)); 16 } 17 void operator *= (const Mat &A){ 18 Mat t; 19 len=A.len; 20 for(int i=1;i<=len;i++){ 21 for(int j=1;j<=len;j++){ 22 for(int k=1;k<=len;k++){ 23 t.s[i][j]=(t.s[i][j]+(s[i][k]*A.s[k][j])%MOD)%MOD; 24 } 25 } 26 } 27 for(int i=1;i<=len;i++){ 28 for(int j=1;j<=len;j++){ 29 s[i][j]=t.s[i][j]; 30 } 31 } 32 } 33 void operator = (const Mat &A){ 34 len=A.len; 35 for(int i=1;i<=len;i++){ 36 for(int j=1;j<=len;j++){ 37 s[i][j]=A.s[i][j]; 38 } 39 } 40 } 41 }; 42 int n,m; 43 Mat Power(Mat A,int p){ 44 Mat ret; 45 ret.len=m+1; 46 for(int i=1;i<=ret.len;i++){ 47 ret.s[i][i]=1; 48 } 49 Mat t; t=A; 50 for(;p;p>>=1){ 51 if(p&1){ 52 ret*=t; 53 } 54 t*=t; 55 } 56 return ret; 57 } 58 int main() 59 { 60 // freopen("harem2.in","r",stdin); 61 Mat A; 62 scanf("%d%d",&n,&m); 63 if(1==n){ 64 printf("%d\n",m+1); 65 } 66 char ch[MAXN]={0}; 67 for(int i=1;i<=m;i++){ 68 scanf("%s",ch+1); 69 for(int j=1;j<=m;j++){ 70 if(‘0‘==ch[j]) 71 A.s[i][j]=1; 72 } 73 } 74 A.len=m+1; 75 for(int i=1;i<=m+1;i++){ 76 A.s[m+1][i]=A.s[i][m+1]=1; 77 } 78 Mat t=Power(A,n-1); 79 ll ans=0; 80 int len=t.len; 81 for(int i=1;i<=len;i++){ 82 for(int j=1;j<=len;j++){ 83 ans=(ans+t.s[i][j])%MOD; 84 } 85 } 86 cout<<ans<<endl; 87 return 0; 88 }
T4:
我当时用莫队算法+暴力,60分

1 #include<cstdio> 2 #include<cstdlib> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #define MAXN 200005 7 using namespace std; 8 struct Ask{ 9 int L,R; 10 int lb,id; 11 int ans; 12 Ask(){ 13 L=R=lb=ans=0; 14 } 15 }; 16 bool comp1(const Ask &p1,const Ask &p2){ 17 if(p1.lb!=p2.lb){ 18 return (p1.lb<p2.lb); 19 } 20 else{ 21 return (p1.R<p2.R); 22 } 23 } 24 bool comp2(const Ask &p1,const Ask &p2){ 25 return (p1.id<p2.id); 26 } 27 Ask s[MAXN]; 28 int n,T; 29 int b[MAXN]; 30 int a[MAXN]; 31 int main() 32 { 33 // freopen("data.in","r",stdin); 34 scanf("%d%d",&n,&T); 35 int size=sqrt(n); 36 for(int i=1;i<=n;i++){ 37 scanf("%d",&a[i]); 38 } 39 for(int i=1;i<=T;i++){ 40 scanf("%d%d",&s[i].L,&s[i].R); 41 s[i].lb=s[i].L/size; 42 s[i].id=i; 43 } 44 sort(s+1,s+T+1,comp1); 45 int x=1,y=0; 46 int t=0; 47 for(int i=1;i<=T;i++){ 48 int L=s[i].L,R=s[i].R; 49 if(x<L){ 50 for(int j=x;j<L;j++){ 51 b[a[j]]--; 52 if(!b[a[j]]){ 53 t=min(t,a[j]); 54 } 55 } 56 } 57 else if(x>L){ 58 for(int j=x-1;j>=L;j--){ 59 if(!b[a[j]]&&t==a[j]){ 60 for(t++;;t++){ 61 if(!b[t]){ 62 break; 63 } 64 } 65 } 66 b[a[j]]++; 67 } 68 } 69 if(y<R){ 70 for(int j=y+1;j<=R;j++){ 71 if(!b[a[j]]&&t==a[j]){ 72 for(t++;;t++){ 73 if(!b[t]){ 74 break; 75 } 76 } 77 } 78 b[a[j]]++; 79 } 80 } 81 else if(y>R){ 82 for(int j=y;j>R;j--){ 83 b[a[j]]--; 84 if(!b[a[j]]){ 85 t=min(t,a[j]); 86 } 87 } 88 } 89 x=L,y=R; 90 s[i].ans=t; 91 } 92 sort(s+1,s+T+1,comp2); 93 for(int i=1;i<=T;i++){ 94 printf("%d\n",s[i].ans); 95 } 96 return 0; 97 }
其实这题并不好写,原因这些数据都是离散的,搞不出来连续的,用数据结构不好维护
于是可以构造出连续的数据:Next[i]=j (a[i]==a[j]&&i<j)
然后按左节点从左到右依次解决,当左节点变化时,相应的j~Next[j]-1用线段树进行更新即可
这样可以用离线算法解决了,转化为典型的离线问题
另:线段树切记开4倍啊QAQ

1 #include<cstdio> 2 #include<cstdlib> 3 #include<algorithm> 4 #include<cstring> 5 #define MAXN 200005 6 #define INF 0x7f7f7f7f 7 using namespace std; 8 int mex[MAXN]; 9 int n,m; 10 int dat[MAXN*4],tag[MAXN*4]; 11 12 void build(int k,int L,int R){ 13 //build:L+1==R return 14 if(L+1==R){ 15 dat[k]=mex[L]; 16 return ; 17 } 18 build(k<<1,L,(L+R)>>1); 19 build(k<<1|1,(L+R)>>1,R); 20 } 21 void pushdown(int k){ 22 int lc=(k<<1),rc=(k<<1|1); 23 dat[lc]=min(dat[lc],tag[k]); 24 dat[rc]=min(dat[rc],tag[k]); 25 tag[lc]=min(tag[lc],tag[k]); 26 tag[rc]=min(tag[rc],tag[k]); 27 tag[k]=INF; 28 } 29 void update(int a,int b,int k,int L,int R,int t){ 30 if(b<=L||R<=a){ 31 return; 32 } 33 else if(a<=L&&R<=b){ 34 dat[k]=min(dat[k],t); 35 tag[k]=min(tag[k],t); 36 } 37 else{ 38 if(tag[k]!=INF){ 39 pushdown(k); 40 } 41 update(a,b,k<<1,L,(L+R)>>1,t); 42 update(a,b,k<<1|1,(L+R)>>1,R,t); 43 } 44 } 45 int find(int x,int k,int L,int R){ 46 if(L+1==R){ 47 return dat[k]; 48 } 49 int mid=(L+R)>>1; 50 if(tag[k]!=INF){ 51 pushdown(k); 52 } 53 if(x<mid){ 54 return find(x,k<<1,L,mid); 55 } 56 else{ 57 return find(x,k<<1|1,mid,R); 58 } 59 } 60 struct Ask{ 61 int L,R; 62 int id,ans; 63 Ask(){ 64 L=R=id=ans=0; 65 } 66 }s[MAXN]; 67 bool comp1(const Ask &p1,const Ask &p2){ 68 return (p1.L<p2.L); 69 } 70 bool comp2(const Ask &p1,const Ask &p2){ 71 return (p1.id<p2.id); 72 } 73 int a[MAXN],b[MAXN]; 74 int Next[MAXN],first[MAXN]; 75 76 int main() 77 { 78 // freopen("T1.in","r",stdin); 79 // freopen("my.out","w",stdout); 80 memset(dat,0x7f,sizeof(dat)); 81 memset(tag,0x7f,sizeof(tag)); 82 // freopen("data.in","r",stdin); 83 scanf("%d%d",&n,&m); 84 for(int i=1;i<=n;i++){ 85 scanf("%d",&a[i]); 86 } 87 for(int i=1;i<=m;i++){ 88 scanf("%d%d",&s[i].L,&s[i].R); 89 s[i].id=i; 90 } 91 int k=0; 92 for(int i=1;i<=n;i++){ 93 b[a[i]]=1; 94 while(b[k]){ 95 k++; 96 } 97 mex[i]=k; 98 } 99 build(1,1,n+1); 100 for(int i=n;i>=1;i--){ 101 Next[i]=first[a[i]]; 102 first[a[i]]=i; 103 if(!Next[i]){ 104 Next[i]=n+1; 105 } 106 } 107 sort(s+1,s+m+1,comp1); 108 int nL=1; 109 for(int i=1;i<=m;i++){ 110 if(nL<s[i].L){ 111 for(int j=nL;j<s[i].L;j++){ 112 update(j,Next[j]-1+1,1,1,n+1,a[j]); 113 } 114 nL=s[i].L; 115 } 116 // for(int j=1;j<=n;j++){ 117 // printf("%d ",find(j,1,1,n+1)); 118 // } 119 // printf("\n"); 120 s[i].ans=find(s[i].R,1,1,n+1); 121 } 122 sort(s+1,s+m+1,comp2); 123 for(int i=1;i<=m;i++){ 124 printf("%d\n",s[i].ans); 125 } 126 return 0; 127 }
标签:模拟 down break div 注意 problem opera alt 一个
原文地址:http://www.cnblogs.com/w-h-h/p/7599769.html