标签：技术分享   2-2   ret   操作   ons   --   简单   表示   names   

第一次知道三分还是在HEOI2017的时候听THU大佬讲题，当时一脸茫然

后来也没碰到过这种题，一直都是用二分（贼啦好使）

不过今天去刷题库里的  [Ahoi2014]宅男计划 的时候，发现需要用三分法，于是就过来填了这个坑QvQ

其实对于二分查找需要满足的单调性，三分是用来查找一个凸性函数 

简单来讲呢，就是函数中存在一个点x是最大（小）值，对于x的左边，满足单调上升（下降），右边满足单调下降（上升），然后我们进行一些“精彩操作”使得不断的逼近这个x点，最后求得答案

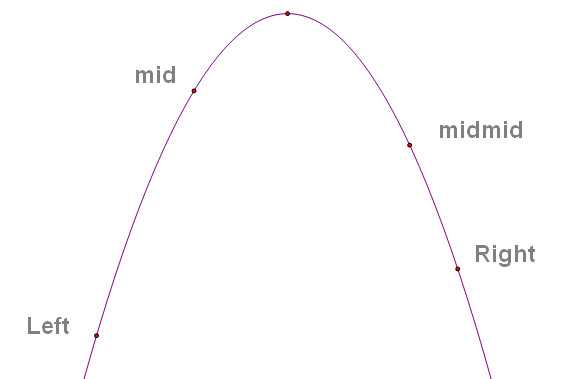
我们对于[L,R]，先找出mid，紧接着再找出[mid,R]的midmid，然后比较两者谁更优，然后舍去不优的

我们不用担心选出来的mid 和 midmid 是在x的同侧还是异侧，因为如果异侧满足（吗）对称性，同侧的话满足单调性，最后都会选出最优解，舍弃不优的。

于是乎，我们就向x逼近了。

我没上来就打 [Ahoi2014]宅男计划 ，而是先去luogu找了个板子

P3382 【模板】三分法

题目描述

如题，给出一个N次函数，保证在范围[l,r]内存在一点x，使得[l,x]上单调增，[x,r]上单调减。试求出x的值。

输入输出格式

输入格式：

第一行一次包含一个正整数N和两个实数l、r，含义如题目描述所示。

第二行包含N+1个实数，从高到低依次表示该N次函数各项的系数。

输出格式：

输出为一行，包含一个实数，即为x的值。四舍五入保留5位小数。

输入输出样例

3 -0.9981 0.5
1 -3 -3 1

-0.41421

说明

时空限制：50ms,128M

数据规模：

对于100%的数据：7<=N<=13

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define pos(i,a,b) for(int i=(a);i<=(b);i++)
#define pos2(i,a,b) for(int i=(a);i>=(b);i--)
#define N 210000
#define LL long long
const double eps=1e-10;
int n;
double l,r;
double a[N];
double check(double x){
	double ans=a[n+1];
	pos2(i,n,1){
		double temp=a[n-i+1];
		pos(j,1,i){
			temp*=x;
		}
		ans+=temp;
	}
	return ans;
}
int main(){
	scanf("%d%lf%lf",&n,&l,&r);
	pos(i,1,n+1){
		scanf("%lf",&a[i]);
	}
	while(l+eps<r){
		double mid=(l+r)/2;
		double mmid=(mid+r)/2;
		if(check(mid)>check(mmid)) r=mmid;
		else l=mid;
	}
	printf("%0.5lf",r);
    return 0;
} 

[知识点]三分查找

标签：技术分享   2-2   ret   操作   ons   --   简单   表示   names   

原文地址：http://www.cnblogs.com/Hallmeow/p/7611816.html