标签:函数 log 去掉 hessian 计算 soft 变换 求导 应用
Softmax回归是Logistic回归在多分类问题上的推广,是有监督的。
回归的假设函数(hypothesis function)为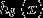 ,我们将训练模型参数
,我们将训练模型参数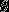 ,使其能够最小化代价函数:
,使其能够最小化代价函数:
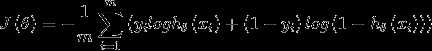
在Softmax回归中,我们解决的是多分类问题,类标y可以取k个不同的值。对于给定的测试输入x,我们想用假设函数针对每一个类别j估算出概率值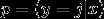 。也就是说,我们想估计x的每一种分类结果的概率。因此,我们的假设函数将要输出一个k维的向量(向量元素的和为1)来表示这k个估计的概率值。具体地说,我们的假设函数
。也就是说,我们想估计x的每一种分类结果的概率。因此,我们的假设函数将要输出一个k维的向量(向量元素的和为1)来表示这k个估计的概率值。具体地说,我们的假设函数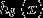 形式如下:
形式如下:
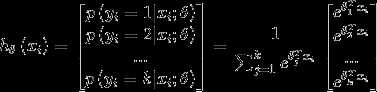
其中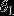 ,
,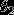 ,···,
,···,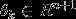 是模型参数。
是模型参数。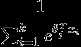 这一项对概率分布进行归一化,使得所有的概率之和为1。
这一项对概率分布进行归一化,使得所有的概率之和为1。
为了方便起见,我们同样使用符号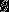 来表示全部的模型参数。在实现softmax回归时,将
来表示全部的模型参数。在实现softmax回归时,将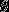 用一个
用一个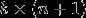 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将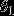 ,
,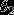 ,···,
,···,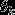 按行罗列起来得到的,如下表示:
按行罗列起来得到的,如下表示:
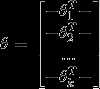
代价函数
现在介绍softmax回归算法的代价函数。在下面的公式中,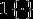 是示性函数,其取值规则为:1{值为真的表达式}=1,1{值为假的表达式}=0。代价函数为:
是示性函数,其取值规则为:1{值为真的表达式}=1,1{值为假的表达式}=0。代价函数为:
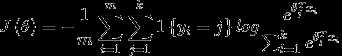
上述公式是logistic回归代价函数的推广。可以看到,softmax代价函数与logistic代价函数在形式上非常类似,只是在softmax代价函数中对类标记的k个可能值进行了累加。注意在softmax回归中将x分类为类别j的概率为:

对于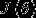 的最小化问题,目前还没有闭式解决。因此,我们使用迭代的优化算法(例如梯度下降法,或L-BFGS)。经过求导,我们得到梯度公式如下:
的最小化问题,目前还没有闭式解决。因此,我们使用迭代的优化算法(例如梯度下降法,或L-BFGS)。经过求导,我们得到梯度公式如下:
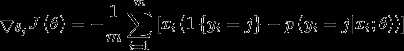
有了上述偏导数公式后,我们就可以将它带入到梯度下降法等算法中,来最小化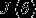 。在实现softmax回归算法时,我们通常会使用上述代价函数的一个改进版本。具体来说,就是和权重衰减(weight decay)一起使用。我们接下来介绍使用它的动机和细节。
。在实现softmax回归算法时,我们通常会使用上述代价函数的一个改进版本。具体来说,就是和权重衰减(weight decay)一起使用。我们接下来介绍使用它的动机和细节。
softmax回归有一个不寻常的特点:它有一个“冗余”的参数集。为了便于阐述这一特点,假设我们从参数向量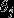 中减去了向量
中减去了向量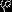 ,这时,每一个
,这时,每一个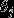 都变成了
都变成了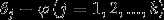 。此时假设函数变成了
。此时假设函数变成了
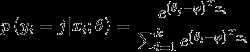

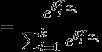
也就是说,从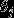 中减去
中减去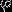 完全不影响假设函数的预测结果。这表明前面的softmax回归模型中存在冗余的参数。更正式一点来说,softmax模型被过度参数化了。对于任意一个用于拟合数据的假设函数 ,可以求出多组参数值,这些参数得到的是完全相同的假设函数
完全不影响假设函数的预测结果。这表明前面的softmax回归模型中存在冗余的参数。更正式一点来说,softmax模型被过度参数化了。对于任意一个用于拟合数据的假设函数 ,可以求出多组参数值,这些参数得到的是完全相同的假设函数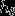 。
。
进一步而言,如果参数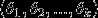 是代价函数
是代价函数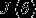 的极小值点,那么
的极小值点,那么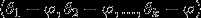 同样也是它的极小值点,其中
同样也是它的极小值点,其中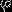 可以为任意向量。因此使
可以为任意向量。因此使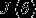 最小化的解不是唯一的。(有趣的是,由于
最小化的解不是唯一的。(有趣的是,由于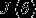 仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是Hessian矩阵是奇异的/不可逆的,这会导致采用牛顿法优化就遇到数值计算的问题。)
仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是Hessian矩阵是奇异的/不可逆的,这会导致采用牛顿法优化就遇到数值计算的问题。)
注意,当 时,我们总是可以将
时,我们总是可以将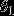 替换为
替换为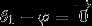 (即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量
(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量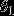 (或者其他
(或者其他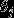 中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的
中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的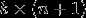 个参数
个参数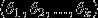 (其中
(其中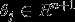 ),我们可以令
),我们可以令 ,只优化剩余的
,只优化剩余的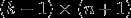 个参数,这样算法依然能够正常工作。
个参数,这样算法依然能够正常工作。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数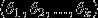 ,而不任意地将某一参数设置为0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决softmax回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决softmax回归的参数冗余所带来的数值问题。
标签:函数 log 去掉 hessian 计算 soft 变换 求导 应用
原文地址:http://www.cnblogs.com/Peyton-Li/p/7612517.html