空间谱专题11：子阵平滑与秩亏缺

标签：tar   htm   lam   images   sha   hle   分解   and   height   

作者：桂。

时间：2017-09-29  21:20:18

链接：http://www.cnblogs.com/xingshansi/p/7612984.html 

未完待续。。。

前言

主要分析在解相干算法中，子阵平滑的有效性。

一、前向平滑

以均匀线阵（ULA）为例，第l个接收阵元的信号为：

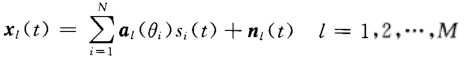
其中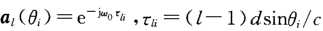，M为阵元数，N为信号个数。

以前向平滑为例：

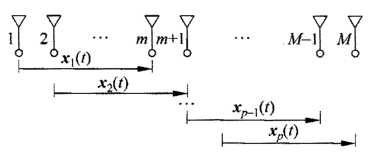
令β = 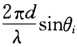，对于第k个子阵有

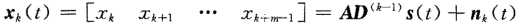
其中D为:

假设信号与噪声不相关，且噪声为白噪声，计算相关矩阵：

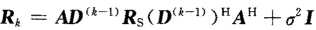
前向平滑修正的协方差矩阵：

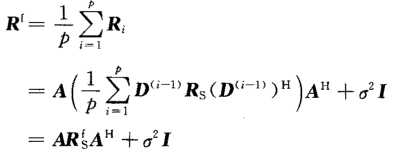
证明：当子阵阵元数m>=N，且当p>=N时，Rf为满秩矩阵。

对于相干情况，Rs的秩为1，故可以用矢量相乘的形式表示：

则

显然C与R_sf的秩是一致的。式中

C可进一步表示为

其中，α为对应信号的幅度，因此该矩阵rank = K

A_L是Vandermonde矩阵：

从而有：

进一步得出结论：

得证。

 上面的推导是教科书中的推导，以两个子阵、两个信号为例，假设两个子阵的间距为D，对应的A可写为：

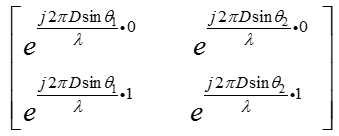
虽然具有Vandermonde结构，但即使入射角度不同，上面的矩阵仍然可能出现rank = 1的情况，只要满足（k为整数）：

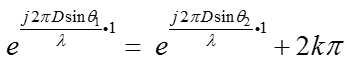
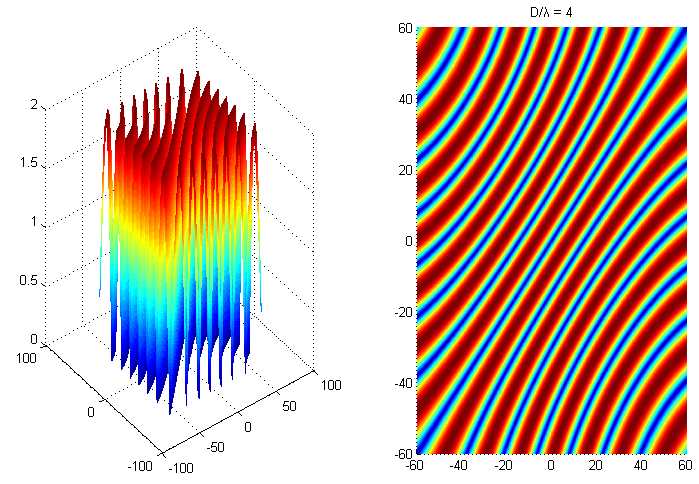
任意取D = 4*λ，theta1、2分别取-60°~60°，仿真结果：

D = 2*λ，进行仿真：

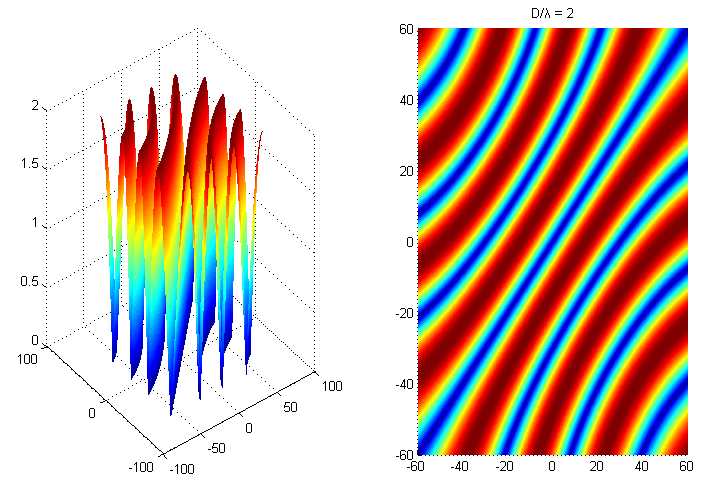
当两个相位差2pi整数倍，如图蓝线所示，此时相关矩阵的秩仍然是亏缺的，此时谱估计解相干失效，这里称蓝色区域为盲区。以MUSIC算法为例，自然也无从谈起矩阵分解以及谱估计。另一方面，D与λ比值的取值越小，则盲区越小。

二、后向平滑算法

三、前后向平滑算法

四、前向、后向、前后向平滑与阵列的关系

五、前后向与非均匀的关系

六、非均匀镜像中坐标点的影响

主要影响D，近而影响盲区

空间谱专题11：子阵平滑与秩亏缺

标签：tar   htm   lam   images   sha   hle   分解   and   height   

原文地址：http://www.cnblogs.com/xingshansi/p/7612984.html