标签:png nbsp out 注意 lower 2-2 push ber 比较
入坑主席树主要是因为昨天考试的后两道题不可改2333 而且觉得这个还挺有用,于是果断入坑
不过蒟蒻的我只是在上午看了看大概思路,下午开的运动会没时间码,于是晚上码了出来。但是目前只会无修改的区间K值问题,加上又比较抽象,思路屡了半天才刚刚醒悟,于是写下来记录一下。
不扯那么多辣鸡套路,直接说思路打法(以k小值为例):
我们先要以权值建一颗线段树,然后每个节点记录的是这个节点管辖的范围内数列中数的个数。
我们需要建好多好多线段树。简单来讲呢,就是[1,1],[1,2]···[1,n]这么多颗,每棵树都是[1,i]按权值建树。
我们要求区间[L,R]中第k小的数,假设我们知道[1,L-1]之间有多少个数比第k小的数小,那么我们只要减去这些数之后在[1, R]区间内第k小的数即是[l, R]区间内的第k小数。
更确切的说,我们要求[L,R]区间内的第k小数 可以 用以[1, R]建立的线段树去减去以[1, L-1] 建立的线段树。(两棵树必须是同构的)
好了现在我们搞到了区间[L,R]这一段对应的线段树,那么我们怎么找k值呢?
若左子树大于k,那么很显然第k小的数在左子树中;若左子树小于k,那么第k小的数在右子树中。
我们来举一个例子:序列 1 2 5 1 3 2 2 5 1 2
我们要求 [5,10]第5小的数
(红色的为个数)
我们建立的[1, l-1] (也就是[1, 4])之间的树为
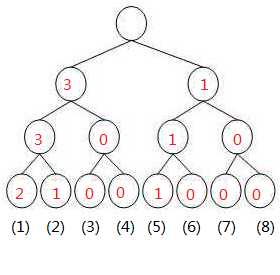
[1, r]也就是[1, 10]的树为
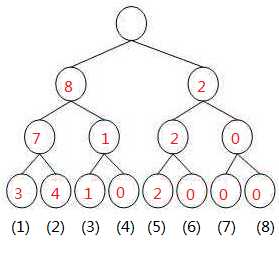
两树相减得到
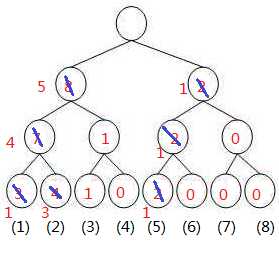
我们来找第5小的数:
发现左子树为5 所以第5小的数在左边, 再往下(左4右1) 发现左边小于5了 ,所以第5小的数在右边 所以第5小的数就是3了
同样的,我们只要建立[1, i] (i是1到n之间的所有值)的所有树,每当询问[l, r]的时候,只要用[1, r]的树减去[1, l-1]的树,再找第k小就好啦
但是,有一个问题发现没有?开这么多树是要炸啊??
我们发现,[1,i]和[1,i+1]所建的线段树只是加了一个a[i]罢了,它们改变的只有a[i]那一条链,其他的是可以共用的!
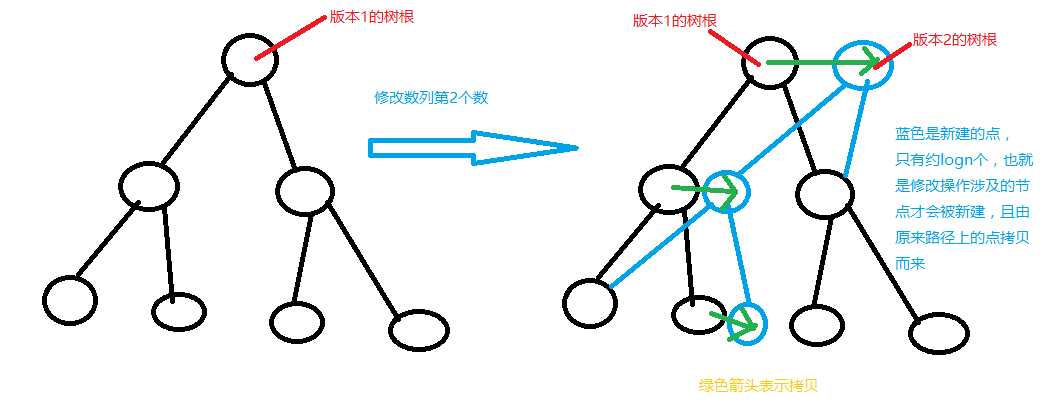
所以就可以这么搞了。但是还是有一个问题:我们按权值建树的话也可能会炸的,所以我们需要离散
我们每次抻出来一个新根节点,加入一下a[i]离散后的值。
我们注意上一个例子,我们找到符合要求的之后,可以直接返回下标3,因为我们是按权值建的树。但是这次我们是按离散之后建的树
所以我们返回的下标 i 是在离散之后排名为 i 的数,我们要返回它原来的值。
不够这里需要注意一下:如果你离散去重了,那么最后返回排名为 i 的数也一定是去重之后的排名为 i 的数
上例题 cogs930 [河南省队2012] 找第k小的数
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define pos(i,a,b) for(int i=(a);i<=(b);i++)
#define N 101000
#include<vector>
#include<algorithm>
int n,m;
int a[N];
vector<int> b;
int find(int x){
return lower_bound(b.begin(),b.end(),x)-b.begin()+1;
}
struct haha{
int lc,rc,num;
}tree[N*20];
int root[N],t;
void build(int num,int &x,int l,int r){
tree[++t]=tree[x];
x=t;
++tree[x].num;
if(l==r) return;
int mid=(l+r)>>1;
if(num<=mid) build(num,tree[x].lc,l,mid);
else build(num,tree[x].rc,mid+1,r);
}
int query(int i,int j,int k,int l,int r){
if(l==r) return l;
int cnt=tree[tree[j].lc].num-tree[tree[i].lc].num;
int mid=(l+r)>>1;
if(k<=cnt) return query(tree[i].lc,tree[j].lc,k,l,mid);
else return query(tree[i].rc,tree[j].rc,k-cnt,mid+1,r);
}
int main(){
//freopen("kthnumber.in","r",stdin);
//freopen("kthnumber.out","w",stdout);
scanf("%d%d",&n,&m);
pos(i,1,n){
scanf("%d",&a[i]);
b.push_back(a[i]);
}
sort(b.begin(),b.end());
b.erase(unique(b.begin(),b.end()),b.end());
tree[0].lc=tree[0].rc=tree[0].num=0;
pos(i,1,n){
root[i]=root[i-1];
build(find(a[i]),root[i],1,n);
}
sort(a+1,a+n+1);
unique(a+1,a+n+1);
pos(i,1,m){
int l,r,k;scanf("%d%d%d",&l,&r,&k);
printf("%d\n",a[query(root[l-1],root[r],k,1,n)]);
}
return 0;
}
标签:png nbsp out 注意 lower 2-2 push ber 比较
原文地址:http://www.cnblogs.com/Hallmeow/p/7616066.html