标签:bbb 空间 src 题目 log class style ble stdio.h
第1行:2个数N和M,中间用空格分隔。N为矩阵的大小,M为M次方。(2 <= N <= 100, 1 <= M <= 10^9) 第2 - N + 1行:每行N个数,对应N * N矩阵中的1行。(0 <= N[i] <= 10^9)
共N行,每行N个数,对应M次方Mod (10^9 + 7)的结果。
2 3 1 1 1 1
4 4 4 4
------------------------------------------------------------
矩阵乘法+快速幂
首先要知道矩阵乘法的运算规则:
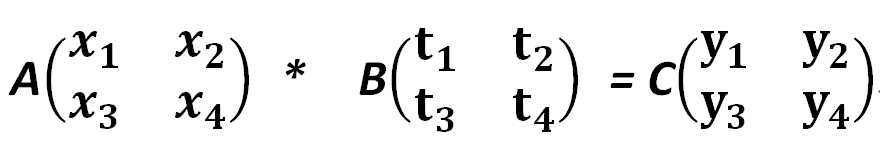
y1=x1t1+x2t3;
y2=x1t2+x2t4;
y3=x3t1+x4t3;
y4=x3t2+x4t4;
即C矩阵(结果矩阵)的第i行第j列的数等于A矩阵第i行的数分别与B矩阵第j列的数的乘积之和。
也可以这样看,A矩阵第i行与B矩阵第j列相交的位置,即计算结果在C矩阵上的位置。
第一次接触矩阵乘法,感觉这个规则有种说不出的奇怪,直到看到这篇博客,加深了我对矩阵乘法的认识。
知道了矩阵的运算法则后,接下来就是在程序中重载矩阵乘法的一些操作。快速幂当然是在重载矩阵运算符(^)中实现,其实现方法依然可以套用其在普通数据类型中的方法(思路都是一样的)。
详细看代码:

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #define maxn 110 5 #define mod 1000000007 6 using namespace std; 7 struct matrix{ 8 long long m[maxn][maxn]; 9 }; 10 int read(); 11 matrix operator * (matrix,matrix); 12 matrix operator ^ (matrix,int); 13 int N,M; 14 int main(){ 15 N=read();M=read(); 16 matrix x,a; 17 for(int i=1;i<=N;i++) 18 for(int j=1;j<=N;j++) 19 x.m[i][j]=read(); 20 a=x^M; 21 for(int i=1;i<=N;i++){ 22 for(int j=1;j<=N;j++) 23 printf("%lld ",a.m[i][j]); 24 putchar(‘\n‘); 25 } 26 return 0; 27 } 28 int read(){ 29 int ans=0,f=1;char c=getchar(); 30 while(‘0‘>c||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();} 31 while(‘0‘<=c&&c<=‘9‘)ans=ans*10+c-48,c=getchar();return ans*f; 32 } 33 matrix operator * (const matrix a,const matrix b){ //重载乘法 34 matrix an; 35 memset(an.m,0,sizeof(an.m)); 36 for(int i=1;i<=N;i++) 37 for(int j=1;j<=N;j++) 38 for(int k=1;k<=N;k++){ 39 an.m[i][j]+=a.m[i][k]*b.m[k][j]%mod; 40 an.m[i][j]%=mod; 41 } 42 return an; 43 } 44 matrix operator ^ (matrix a,int b){ //重载幂运算 45 matrix an; 46 for(int i=1;i<=N;i++) //初始化an,即累乘变量 47 for(int j=1;j<=N;j++) 48 an.m[i][j]=(i==j); //注意这里应为i==j,而不是 1,跟矩阵的运算法则有关吧 49 while(b){ //快速幂 50 if(b&1) an=an*a; 51 a=a*a; 52 b>>=1; 53 } 54 return an; 55 }
标签:bbb 空间 src 题目 log class style ble stdio.h
原文地址:http://www.cnblogs.com/lpl-bys/p/7618027.html