标签:向量 预测图 span 网络 参数 src 变化 构建 技术分享
一、二分类问题与logistic 回归
回归问题
“回归”一词源自英国科学弗朗西斯·高尔顿(Francis Galton),他还是著名的生物学家、进化论奠基人查尔斯·达尔文(Charles Darwin)的表弟。高尔顿发现,虽然有一个趋势——父母高,儿女也高;父母矮,儿女也矮,但给定父母的身高,儿女辈的平均身高却趋向于或者“回归”到全体人口的平均身高。换句话说,即使父母双方都异常高或者异常矮,儿女的身高还是会趋向于人口总体的平均身高。这也就是所谓的普遍回归规律。高尔顿的这一发现被他的朋友,英国数学家、数理统计学的创立者卡尔·皮克逊(Karl Pearson)所证实。皮尔逊收集了一些家庭的1000多名成员的身高记录,发现对于一个父亲高的群体,儿辈的平均身高低于他们父辈的身高;而对于一个父亲矮的群体,儿辈的平均身高则高于其父辈的身高。这样就把高的和矮的儿辈一同“回归”到所有男子的平均身高,用高尔顿的话说,这是“回归到中等”
回归分析是被用来研究一个被解释变量(Explained Variable)与一个或多个解释变量(Explanatory Variable)之间关系的统计技术。被解释变量有时也被称为因变量(Dependent Variable),与之相对应地,解释变量也被称为自变量(Independent Variable)。回归分析的意义在于通过重复抽样获得的解释变量的已知或设定值来估计或者预测被解释变量的总体均值。
下面举一个简单的线性回归实例来了解其中的原理:
通过调查我们记录了父辈身高与子辈身高的几组数据。
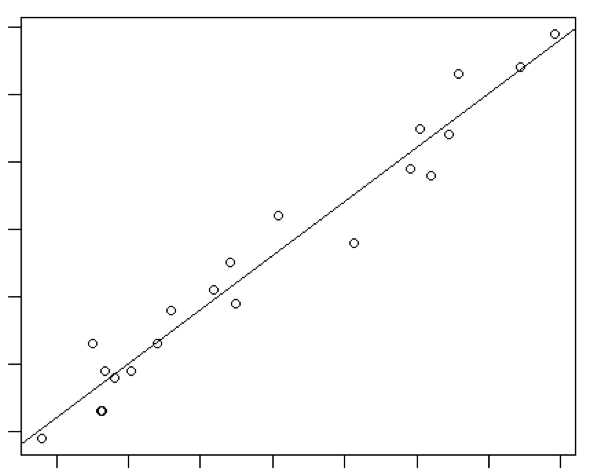
通过作图可以得知子辈身高与父辈身高存在线性关系,于是我们可以将子辈身高作为被解释变量 y,父辈身高作为解释变量x来构建线性回归模型:
y=wx+b
其中w、b表示回归参数。我们只要找到了符合条件的w、b,就可以通过这个回归模型预测y的值。
更一般的,如果我们的解释变量不止一个,且他们与被解释变量存在线性关系,我们就可以构建这样的回归模型:
y=w1x1+w2x2+w3x3+···+wnxn+b
Logistic回归
线性回归解决了连续变量之间的关系问题,但是现实生活中也会存在许多离散的分类问题。例如我们要判别一张图片的内容是不是“猫”,这里我们只希望预测结果为“是”或者“否”,那么我们就要对一般的回归进行改造。于是便出现了logistic regression模型:
如下图,我们希望通过数学模型很好的区分下面的点该分为哪一区域(类),假设为0和1。
这个问题中,我们输入点的坐标是可以连续变化的,但我们希望得到到的结果是离散的,于是我们可以构建logistic回归模型来预测图中的点属于哪一类。
我们假设可以找到一条直线可以很好的区分两个区域,首先我们求横纵坐标(x1,x2)的线性和(w1、w2、b是回归参数):
z=w1x1+w2x2+b
将z的值通过Sigmoid函数映射到0~1之间
g(z)=\frac{1}{1+e^{-z}}
g(z)的值我们将它看做是(x1,x2)对应的z属于0还是1这一类的概率,假设P0、P1分别 代表属于0、1的概率,则有
P1=g(z)
P0=1-g(z)
于是通过比较概率的大小我们就能确定(x1,x2)对应的点属于哪一类了。其中P=0.5对应的点所在的直线就成为决策边间(z=w1x1+w2x2+b,g(z)=0.5)
如果找到了合适的回归参数,上述模型就能很好的解决这类问题了,接下来看看如何通过学习算法找到这些参数:
我们将所有参数向量话表示
\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+······+\theta_{n}x_{n}=\sum_{i=1}^{n}\theta_{i}x_{i}=\theta^{T}X
预测函数
$h_{\theta }(x)=g(\theta ^{T}x)=\frac{1}{1+e^{-\theta ^{T}x}}$
P(y=1|X)=h_{\theta }(x)
p(y=0|X)=1-h_{\theta }(x)
标签:向量 预测图 span 网络 参数 src 变化 构建 技术分享
原文地址:http://www.cnblogs.com/skywangch/p/7620328.html