标签：image 时间 本质 结果 png order 技术分享 垃圾 泊松分布
原文链接：http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html
一般来说，回归不用在分类问题上，因为回归是连续型模型，而且受噪声影响比较大。如果非要使用回归算法，可以使用logistic回归。
logistic回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0和1上。
logistic回归的假设函数如下，线性回归假设函数只是\(\theta&^x\)。
\[h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}\]
\[g(z)=\frac{1}{1+e^{-z}}\]
logistic回归用来分类0/1问题，也就是预测结果属于0或者1的二值分类问题。这里假设了二值满足伯努利分布，也就是
当然假设它满足泊松分布、指数分布等等也可以，只是比较复杂，后面会提到线性回归的一般形式。
与第7节一样，仍然求的是最大似然估计，然后求导，得到迭代公式结果为
可以看到与线性回归类似，只是
换成了
，而
实际上就是
经过g(z)映射过来的。
第7和第9节使用的解最大似然估计的方法都是求导迭代的方法，这里介绍了牛顿下降法，使结果能够快速的收敛。
当要求解
时，如果f可导，那么可以通过迭代公式
来迭代求解最小值。
当应用于求解最大似然估计的最大值时，变成求解最大似然估计概率导数
的问题。
那么迭代公式写作
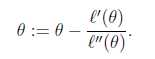
当θ是向量时，牛顿法可以使用下面式子表示
其中
是n×n的Hessian矩阵。
牛顿法收敛速度虽然很快，但求Hessian矩阵的逆的时候比较耗费时间。
当初始点X0靠近极小值X时，牛顿法的收敛速度是最快的。但是当X0远离极小值时，牛顿法可能不收敛，甚至连下降都保证不了。原因是迭代点Xk+1不一定是目标函数f在牛顿方向上的极小点。
之所以在logistic回归时使用
的公式是由一套理论作支持的。
这个理论便是一般线性模型。
首先，如果一个概率分布可以表示成
时，那么这个概率分布可以称作是指数分布。
伯努利分布，高斯分布，泊松分布，贝塔分布，狄特里特分布都属于指数分布。
在logistic回归时采用的是伯努利分布，伯努利分布的概率可以表示成
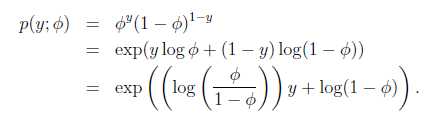
其中
得到
这就解释了logistic回归时为了要用这个函数。
一般线性模型的要点是
1） 
满足一个以
为参数的指数分布，那么可以求得
的表达式。
2） 给定x，我们的目标是要确定
，大多数情况下
，那么我们实际上要确定的是
，而
。（在logistic回归中期望值是
，因此h是
；在线性回归中期望值是
，而高斯分布中
，因此线性回归中h=
）。
3） 
最后举了一个利用一般线性模型的例子。
假设预测值y有k种可能，即y∈{1,2,…,k}
比如k=3时，可以看作是要将一封未知邮件分为垃圾邮件、个人邮件还是工作邮件这三类。
定义
那么
这样
即式子左边可以有其他的概率表示，因此可以当作是k-1维的问题。
为了表示多项式分布表述成指数分布，我们引入T(y)，它是一组k-1维的向量，这里的T(y)不是y，T(y)i表示T(y)的第i个分量。
应用于一般线性模型，结果y必然是k中的一种。1{y=k}表示当y=k的时候，1{y=k}=1。那么p(y)可以表示为
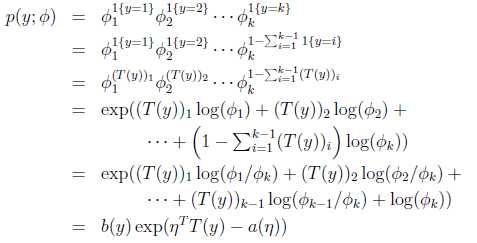
其实很好理解，就是当y是一个值m（m从1到k）的时候，p(y)=
，然后形式化了一下。
那么
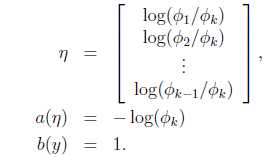
最后求得
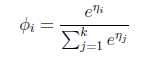
而y=i时
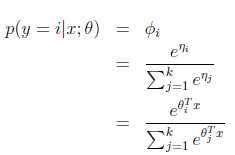
求得期望值
那么就建立了假设函数，最后就获得了最大似然估计
对该公式可以使用梯度下降或者牛顿法迭代求解。
解决了多值模型建立与预测问题。
标签：image 时间 本质 结果 png order 技术分享 垃圾 泊松分布
原文地址：http://www.cnblogs.com/mikewolf2002/p/7622099.html
