561. Array Partition I【easy】

标签：empty   put   tput   osi   解法   ase   att   which   sort   

561. Array Partition I【easy】

Given an array of 2n integers, your task is to group these integers into n pairs of integer, say (a1, b1), (a2, b2), ..., (an, bn) which makes sum of min(ai, bi) for all i from 1 to n as large as possible.

Example 1:

Input: [1,4,3,2]

Output: 4
Explanation: n is 2, and the maximum sum of pairs is 4 = min(1, 2) + min(3, 4).

Note:

1. n is a positive integer, which is in the range of [1, 10000].
2. All the integers in the array will be in the range of [-10000, 10000].

解法一：

 1 class Solution {
 2 public:
 3     int arrayPairSum(vector<int>& nums) {
 4         if (nums.empty()) {
 5             return 0;
 6         }
 7         
 8         sort(nums.begin(), nums.end());
 9         
10         int sum = 0;
11         for (int i = 0; i < nums.size(); i += 2) {
12             sum += nums[i];
13         }
14         
15         return sum;
16     }
17 };

为了不浪费元素，先排序，这样可以保证min加出来为max

比如[1, 9, 2, 4, 6, 8]

如果按顺序来的话，1和9就取1，2和4就取2，6和8就取6，显而易见并不是最大，原因就是9在和1比较的时候被浪费了，9一旦浪费就把8也给影响了，所以要先排序

@shawngao 引入了数学证明的方法，如下：

Let me try to prove the algorithm...

1. Assume in each pair i, bi >= ai.
2. Denote Sm = min(a1, b1) + min(a2, b2) + ... + min(an, bn). The biggest Sm is the answer of this problem. Given 1, Sm = a1 + a2 + ... + an.
3. Denote Sa = a1 + b1 + a2 + b2 + ... + an + bn. Sa is constant for a given input.
4. Denote di = |ai - bi|. Given 1, di = bi - ai. Denote Sd = d1 + d2 + ... + dn.
5. So Sa = a1 + a1 + d1 + a2 + a2 + d2 + ... + an + an + di = 2Sm + Sd => Sm = (Sa - Sd) / 2. To get the max Sm, given Sa is constant, we need to make Sd as small as possible.
6. So this problem becomes finding pairs in an array that makes sum of di (distance between ai and bi) as small as possible. Apparently, sum of these distances of adjacent elements is the smallest. If that‘s not intuitive enough, see attached picture. Case 1 has the smallest Sd.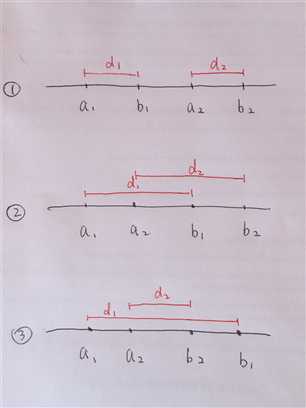

561. Array Partition I【easy】

标签：empty   put   tput   osi   解法   ase   att   which   sort   

原文地址：http://www.cnblogs.com/abc-begin/p/7623481.html