标签:images using 容斥原理 人才 根据 mat 方式 复杂 read
1 数学课
程序文件名: number.c/cpp/pas
输入文件: number.in
输出文件: number.out
时间限制: 1s
空间限制: 256Mb
题目描述
数学课上,老师在黑板上写了n个数,然后让大家做一个游戏:每次擦掉黑板上的两个数,然后在黑板上写下这两个数的乘积加一,直到最后只有一个数。同学们做了几次这个游戏之后,发现最终剩下的数大小不一。同学们十分好奇,但老师说:“如果你们能保证剩下的数比我玩的时候剩下的数要小或者相等,那我就告诉你们原因。”同学们现在十分想知道原因,你能帮帮他们吗?
输入格式
第一行有一个正整数n,代表数字的个数。
下一行有n个正整数a1; a2; :::; an,表示老师在黑板上写下的数。
输出格式
一个数,表示同学们最后应该剩下的数。对109 + 7取模。
样例
输入 输出
3 15
2 2 3
样例解释:先将2和3擦掉,写下7,再将7和2擦掉,写下15。
数据范围
对于20%的数据,n≤8 ,????≤10
对于40%的数据,n≤8
对于100%的数据,n≤200 ,????≤10^9
简单模拟+贪心。
我们可以证明每次去两个最大的数相乘一定比其余做法优。
可以通过二叉树说明。
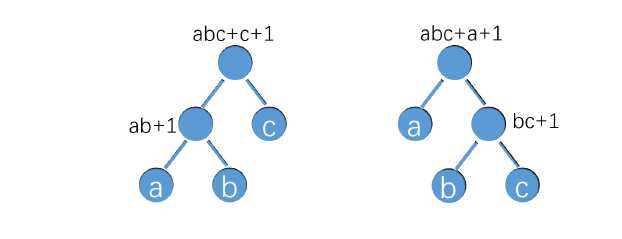
假设a为左图最小值,则左图->右图可以发现右图更小。
进行类似操作,可以发现最小值通过被替换一直会留在二叉树中,而最大值则会被擦去。
也就是说,最小值总是最后擦去,而最大值被不断删除。
以此类推,每次的做法就是取两个最大值相乘。
该做法是O(nlogn)。
1 #include<cstdio> 2 #include<algorithm> 3 #define MODE 1000000007 4 #define MAXN 205 5 #define ll long long 6 using namespace std; 7 int a[MAXN]; 8 int n; 9 ll ans=0; 10 inline int read(){ 11 int x=0,f=1;char ch=getchar(); 12 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} 13 while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} 14 return x*f; 15 } 16 bool cmp(int x,int y){return x>y;} 17 int main(){ 18 freopen("number.in","r",stdin); 19 freopen("number.out","w",stdout); 20 n=read(); 21 for(int i=1;i<=n;i++) a[i]=read(); 22 sort(a+1,a+n+1,cmp); 23 //for(int i=1;i<=n;i++) printf("a[i]=%d\n",a[i]); 24 ans=a[1]; 25 for(int i=2;i<=n;i++){ 26 ans*=a[i];ans+=1;ans%=MODE; 27 } 28 printf("%d",ans); 29 return 0; 30 }
遗传病(disease,2s,256M)
【题目描述】
众所周知,近亲结婚的后代患遗传病的概率会大大增加。如果某一基因按常染色体隐性遗传方式,其子女就可能因为是突变纯合子而发病。因此,近亲婚配增加了某些常染色体隐性遗传疾病的发生风险。
现在有n个人,每个人都有一个遗传特征值a_i,假设第i个人和j个人结婚,那么风险系数为gcd?(a_i,a_j),法律规定只有风险系数为1时两个人才能结婚。
F同学开了一个婚姻介绍所,这n个人可能会来登记,当然也有可能登记后取消,也有可能取消后再登记。F同学的任务就是,求出当前所有登记的人中,有多少对人是可以结婚的。
刚开始所有人都没有登记。
为出题需要,不考虑性别,基因突变和染色体变异等QAQ。
【输入格式】
从disease.in中读入。
第一行两个整数n和q,n表示人数,q表示登记和登出的总次数。
第二行n个整数a_1,a_2,…,a_n,意义如上所述。
接下来q行,每行一个整数x。如果当前第x个人没有登记,那么第x个人登记;如果当前第x个人已经登记了,那么其取消登记。
【输出格式】
输出到disease.out中。
一共q行,第i行表示第i个操作后,当前所有登记的人中有多少对人是可以结婚的。
【样例一输入】
5 6
1 2 3 4 6
1
2
3
4
5
1
【样例一输出】
0
1
3
5
6
2
【子任务】
30%数据,1<=n,q<=1000
100%数据,1<=n,q<=100000,1<=ai<=500000
本题考察容斥原理。
30%数据,每加入或删除一个数,扫一下已经登记的人求一下gcd即可,时间复杂度O(n^2)
100%数据,考虑容斥原理。
比如加入一个数30,那么60的质因数集合为{2,3,5}(重复的去掉)
两个数互质等价于质因数集合交集问空集。
记|S|为当且已登记的人中质因数集合的子集有S的人数,其中S是一个质因数集合
特别地,记|{1}|=当前已登记的人数
与30互质的个数=|{1}|-|{2}|-|{3}|-|{5}|+|{2,3}|+|{2,5}|+|{3,5}|-|{2,3,5}|
因为2*3*5*7*11*13*17=510510>500000,所以每个数最多只有6个质因数(重复的去掉)
2^6=64,时间复杂度为O(64n)。
还没有A。
本题也是莫比乌斯反演。
1 //std 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cassert> 5 #include<iostream> 6 #include<fstream> 7 #include<algorithm> 8 #include<cstring> 9 #include<string> 10 #include<cmath> 11 #include<queue> 12 #include<stack> 13 #include<map> 14 #include<utility> 15 #include<set> 16 #include<bitset> 17 #include<vector> 18 #include<functional> 19 #include<deque> 20 #include<cctype> 21 #include<climits> 22 #include<complex> 23 #include<bits/stdc++.h> 24 #include<ctime> 25 #include<ext/rope> 26 27 using namespace __gnu_cxx; 28 using namespace std; 29 30 typedef long long LL; 31 typedef double DB; 32 typedef pair<int,int> PII; 33 typedef pair<DB,DB> PDD; 34 typedef complex<DB> CP; 35 typedef vector<int> VI; 36 37 #define mmst(a,v) memset(a,v,sizeof(a)) 38 #define mmcy(a,b) memcpy(a,b,sizeof(a)) 39 #define fill(a,l,r,v) fill(a+l,a+r+1,v) 40 #define re(i,a,b) for(i=(a);i<=(b);i++) 41 #define red(i,a,b) for(i=(a);i>=(b);i--) 42 #define fi first 43 #define se second 44 #define mp(a,b) make_pair(a,b) 45 #define pb(a) push_back(a) 46 #define two(k) (1<<(k)) 47 #define SZ(x) (int(x.size())) 48 #define all(x) (x).begin(),(x).end() 49 #define ire(i,v,x) for(i=0,v=i<SZ(x)?x[i]:0;i<SZ(x);v=x[++i]) 50 #define ls (rt<<1) 51 #define rs (rt<<1|1) 52 #define MID ((l+r)>>1) 53 54 template<class T>inline T sqr(T x){return x*x;} 55 template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;} 56 template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;} 57 58 inline int sgn(DB x){if(abs(x)<1e-9)return 0;return(x>0)?1:-1;} 59 const DB Pi=acos(-1.0); 60 61 //void enlargestack(){int size=256<<10;char *p=(char*)malloc(size)+size;__asm__("movl %0, %%esp\n"::"r"(p));} 62 63 int gint() 64 { 65 int res=0;bool neg=0;char z; 66 for(z=getchar();z!=EOF && z!=‘-‘ && !isdigit(z);z=getchar()); 67 if(z==EOF)return 0; 68 if(z==‘-‘){neg=1;z=getchar();} 69 for(;z!=EOF && isdigit(z);res=(res<<3)+(res<<1)+z-‘0‘,z=getchar()); 70 return (neg)?-res:res; 71 } 72 LL gll() 73 { 74 LL res=0;bool neg=0;char z; 75 for(z=getchar();z!=EOF && z!=‘-‘ && !isdigit(z);z=getchar()); 76 if(z==EOF)return 0; 77 if(z==‘-‘){neg=1;z=getchar();} 78 for(;z!=EOF && isdigit(z);res=res*10+z-‘0‘,z=getchar()); 79 return (neg)?-res:res; 80 } 81 82 const int maxn=210000; 83 const int maxm=510000; 84 85 int n,q,m; 86 int a[maxn]; 87 int cnt,flag[maxm],prime[maxm],p[maxm]; 88 vector<int> b[maxn]; 89 int in[maxn]; 90 int table[maxm]; 91 LL res; 92 93 void init() 94 { 95 int i,j; 96 re(i,2,m) 97 { 98 if(!flag[i])prime[++cnt]=i; 99 for(j=1;j<=cnt && i*prime[j]<=m;j++) 100 { 101 flag[i*prime[j]]=1; 102 p[i*prime[j]]=prime[j]; 103 if(i%prime[j]==0)break; 104 } 105 } 106 re(i,1,n) 107 { 108 int x=a[i]; 109 while(x!=1) 110 { 111 int t=flag[x]?p[x]:x; 112 b[i].pb(t); 113 while(x%t==0)x/=t; 114 } 115 } 116 } 117 118 void dfs(int x,int k,int mult,int f) 119 { 120 if(k==SZ(b[x])) 121 { 122 res+=in[x]==1?table[mult]*in[x]*f:(table[mult]-1)*in[x]*f; 123 table[mult]+=in[x]; 124 return; 125 } 126 dfs(x,k+1,mult*b[x][k],-f); 127 dfs(x,k+1,mult,f); 128 } 129 130 int main() 131 { 132 freopen("disease.in","r",stdin); 133 freopen("disease.out","w",stdout); 134 int i; 135 n=gint();q=gint(); 136 re(i,1,n)a[i]=gint(),upmax(m,a[i]); 137 init(); 138 fill(in,1,n,1); 139 while(q--) 140 { 141 int x=gint(); 142 dfs(x,0,1,1); 143 in[x]=-in[x]; 144 printf("%I64d\n",res); 145 } 146 return 0; 147 }
瓜分领土(2s,512MB)
石头、剪刀和布闹别扭了,他们要分家。
他们生活在一个离散的一维空间里,简单点说,他们拥有在一条直线上的N间房子,每间房子有一个风水值(有正有负)。
然后,他们决定将这N间房子分成非空的三个连续段,从左到右数,第一段的房子全部属于石头,第二段的房子全部属于剪刀,第三段的房子全部属于布。
由于他们希望公平,并且又由于剪刀是他们的老大哥,他们决定根据这些条件制定了一个评判标准:
设石头拥有的房子的风水值和为a,剪刀拥有的房子的风水值和为b,布拥有的房子的风水值和为c,剪刀拥有n间房子。
那么通过给定一个参数x。
那么,这种分配的合理值就是max(a,b,c)-min(a,b,c)+x*n.
合理值越小,表示这种分配越合理。
因此,我们现在就是要求出这个最小的合理值。
输入格式
第一行一个正整数N。
第二行有N个整数,表示房子的风水值,按从左到右的顺序给出。
第三行一个整数x。
输出格式
一行一个整数,表示最小的合理值。
输入样例:
4
1 1 1 1
-1
输出样例:
-1
数据范围:
对于30%的数据,N<=10.
对于70%的数据,N<=1000.
对于100%的数据,N<=100000,保证所有运算结果在long long范围内。
线段树+二分+离散+枚举+数学结论。
留坑。以及正解写挂60<暴力O(n^2)的惨案。
标签:images using 容斥原理 人才 根据 mat 方式 复杂 read
原文地址:http://www.cnblogs.com/drizzly/p/7623971.html