标签：完全   es2017   原来   部署   技术   cpp   black   不难   div   

A-航运调度：

一道比较裸的三分题，令$F(t)$为$t$时刻船两两之间距离的最大值，直接三分求$F(t)$在$[0,+\infty)$的最小值即可。

时间复杂度：$O(n^2 log n)$。

（其实你问我为什么它是个单峰函数我也不会证）

B-防线：

首先有一个显然的结论，如果$x$处有破绽，那么包含$x$的区间的防具和一定是奇数。于是乎在$[1,2^{31}-1]$上二分即可找到有破绽的位置。

求$[a,b]$上防具和时仅需将所有的部署都扫一遍。

sum=0;
for(i=1;i<=n;i++) {
	sum+=(b-S[i])/D[i]+1;
	if(a-1>=S[i]) sum-=(x-1-S[i])/D[i]+1;
}

l=1;r=(1<<31)-1;
while(l<r) {
  m=l+r>>1;
  if(getSum(l,m)&1) r=m;
  else l=m+1;
}

核心代码如上，直抄必错。注意判断。

时间复杂度：$O(NTlog(2^{31}-1))=O(NT)$

C-分形之城：

其实只要把图看懂了这道题还是很好想的。

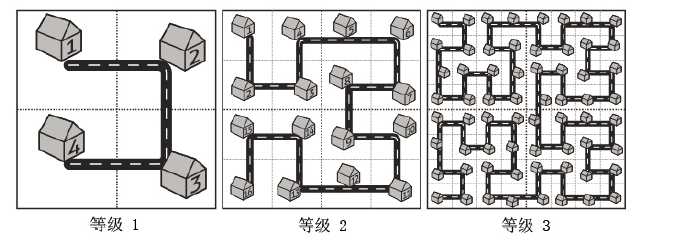
显然每个等级都可以分成四块，每块里面的编号是连续的。

设每个等级的城区为$T_k$，$k$为等级。我们要求编号为$i$的街区在$T_k$中的位置$(x,y)$，可以想办法先求出$i$在它所在的块中的位置，也就是$T_{k-1}$中的位置$(x‘,y‘)$，再想办法求$(x,y)$。至此我们已经把问题规模缩小了。现在的问题是如何把$(x‘,y‘)$转化为$(x,y)$。

为讨论方便，我们令$(x,y)$指的是从左上角算起，第$x$行第$y$列的街区编号为$i$。

那么分情况讨论。

• 若$i$在左上角的块中。

  计数也是从左上角开始的，但方向翻转了一下，所以

  $(x,y)=(y‘,x‘)$

• 若$i$在右上角的块中。

  其实这跟原来是完全没区别的，仅需平移一下。

  $(x,y)=(x‘,y‘+len)$

• 若$i$在右下角的块中。

  同上，有

  $(x,y)=(x‘+len,y‘+len)$

• 若$i$在左下角的块中。

  这个要麻烦一点，它是从右下角开始计数的，但也不难推出

  $(x,y)=(len*2+1-y‘,len+1-x‘)$

讨论清楚了就很好实现了。（$len$为其中一块的边长）

但这道题有不少坑点，首先编号什么的要开$long \ \ long$。而且不能先乘10再算距离否则$long \ \ long$会溢出，此处感谢$@OBlack$。（如果你用$double$当我没说）

时间复杂度：$O(NT)$

NK分治赛题解

标签：完全   es2017   原来   部署   技术   cpp   black   不难   div   

原文地址：http://www.cnblogs.com/SilentMelody/p/7624799.html