标签:gif str name aac sig 利用 i++ mat 运算
题意 : 长度不超过L,只由小写字母组成的,至少包含一个词根的单词,一共可能有多少个呢?这里就不考虑单词是否有实际意义。
比如一共有2个词根 aa 和 ab ,则可能存在104个长度不超过3的单词,分别为
(2个) aa,ab,
(26个)aaa,aab,aac...aaz,
(26个)aba,abb,abc...abz,
(25个)baa,caa,daa...zaa,
(25个)bab,cab,dab...zab。
分析 : 这题和 POJ 2778 非常相似,如果没有做过 POJ 2778 建议先去搞定那道题。此题难点就在于这个是要求不超过 L 长度包含词根的单词,根据解决 POJ 2778 的经验,我们可以得出 答案 = 总单词种类数 - 不包含词根的单词数。首先总单词数可以很容易想到为 261 + 262 + 263 + ..... + 26L ,而不包含词根的单词总数可以这样得到 ==> 假设原 Trie 图构建出来的状态矩阵为 A ,那么同样的我们需要构造一个幂和即 A1 + A2 + A3 + ..... + AL 然后最后的答案便是 ∑AL(0, i) ( i ∈ 1~矩阵长度 ) ,那怎么去构造这两个幂和呢?
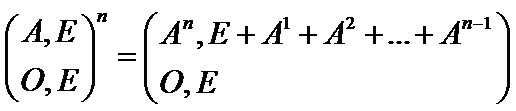
只要利用这个公式即可,用原矩阵 + 单位矩阵 + 零矩阵构造出新矩阵,最后右上角的矩阵便是幂和的矩阵!
这里还有一点要注意,就是对于 2^64次方求模有一个很巧的方法,也就是直接定义为 unsigned long long (范围 : 0 ~ 2^64 -1),溢出就相当于求模了!

#include<string.h> #include<stdio.h> #include<iostream> #include<queue> #define ULL unsigned long long using namespace std; const int Max_Tot = 1e2 + 10; const int Letter = 26; int maxn;///矩阵的大小 char S[11]; struct mat{ ULL m[111][111]; }unit, M; mat operator * (mat a, mat b){ mat ret; for(int i=0; i<maxn; i++){ for(int j=0; j<maxn; j++){ ret.m[i][j] = (ULL)0; for(int k=0; k<maxn; k++){ ret.m[i][j] += a.m[i][k]*b.m[k][j]; } } } return ret; } inline void init_unit() { for(int i=0; i<maxn; i++) unit.m[i][i] = 1; } mat pow_mat(mat a, long long n){ mat ret = unit; while(n){ if(n&1) ret = ret * a; a = a*a; n >>= 1; } return ret; } struct Aho{ struct StateTable{ int Next[Letter]; int fail, flag; }Node[Max_Tot]; int Size; queue<int> que; inline void init(){ while(!que.empty()) que.pop(); memset(Node[0].Next, 0, sizeof(Node[0].Next)); Node[0].fail = Node[0].flag = 0; Size = 1; } inline void insert(char *s){ int now = 0; for(int i=0; s[i]; i++){ int idx = s[i] - ‘a‘; if(!Node[now].Next[idx]){ memset(Node[Size].Next, 0, sizeof(Node[Size].Next)); Node[Size].fail = Node[Size].flag = 0; Node[now].Next[idx] = Size++; } now = Node[now].Next[idx]; } Node[now].flag = 1; } inline void BuildFail(){ Node[0].fail = -1; for(int i=0; i<Letter; i++){ if(Node[0].Next[i]){ Node[Node[0].Next[i]].fail = 0; que.push(Node[0].Next[i]); }else Node[0].Next[i] = 0;///必定指向根节点 } while(!que.empty()){ int top = que.front(); que.pop(); if(Node[Node[top].fail].flag) Node[top].flag = 1; for(int i=0; i<Letter; i++){ int &v = Node[top].Next[i]; if(v){ que.push(v); Node[v].fail = Node[Node[top].fail].Next[i]; }else v = Node[Node[top].fail].Next[i]; } } } inline void BuildMatrix(){ for(int i=0; i<Size; i++) for(int j=0; j<Size; j++) M.m[i][j] = 0; for(int i=0; i<Size; i++){ for(int j=0; j<Letter; j++){ if(!Node[i].flag && !Node[ Node[i].Next[j] ].flag) M.m[i][Node[i].Next[j]]++; } } maxn = Size; } }ac; ULL GetSum(long long num){ mat ret; ret.m[0][0] = 26; ret.m[0][1] = 1; ret.m[1][0] = 0; ret.m[1][1] = 1; int tmp = maxn; maxn = 2; ret = pow_mat(ret, ++num); maxn = tmp; return ret.m[0][1]-1; } ULL GetElimination(long long num){ mat tmp; for(int i=0; i<maxn; i++)///左上角 为 原矩阵 for(int j=0; j<maxn; j++) tmp.m[i][j] = M.m[i][j]; for(int i=0; i<maxn; i++)///右上角 为 单位矩阵 for(int j=maxn; j<(maxn<<1); j++) tmp.m[i][j] = (i+maxn == j); for(int i=maxn; i<(maxn<<1); i++)///左下角 为 零矩阵 for(int j=0; j<maxn; j++) tmp.m[i][j] = 0; for(int i=maxn; i<(maxn<<1); i++)///右下角 为 单位矩阵 for(int j=maxn; j<(maxn<<1); j++) tmp.m[i][j] = (i==j); int Temp = maxn; maxn <<= 1;///先将原本矩阵的大小放大一倍进行快速幂运算,这个和我快速幂的写法有关 tmp = pow_mat(tmp, ++num); ULL ret = (ULL)0; maxn = Temp;///再回复成原来大小 for(int i=maxn; i<(maxn<<1); i++)///右上角的矩阵就是幂和了 ret += tmp.m[0][i]; return (--ret);///需要 -1 } int main(void) { int n, m; while(~scanf("%d %d", &m, &n)){ ac.init(); for(int i=0; i<m; i++){ scanf("%s", S); ac.insert(S); } ac.BuildFail(); ac.BuildMatrix(); init_unit(); ULL Tot = GetSum((long long)n);///注意是传long long不然会爆int ULL Elimination = GetElimination((long long)n); cout<<Tot-Elimination<<endl; } return 0; }
HDU 2243 考研路茫茫——单词情结 ( Trie图 && DP && 矩阵构造幂和 )
标签:gif str name aac sig 利用 i++ mat 运算
原文地址:http://www.cnblogs.com/Rubbishes/p/7629830.html