标签:src 路径 http 关系 几何 lca images end 介绍
在学习平面几何的时候, 我们介绍了点, 直线和圆, 随后就研究了它们之间的一些数量关系.
现在的载体变成了树. 对于一棵树, 我们定义了点和路径, 那么不妨可以研究一下点与点的距离, 点到路径的距离, 路径到路径的距离.
$dist(x, y) = d[x] + d[y] - d[LCA(x, y)]$ .
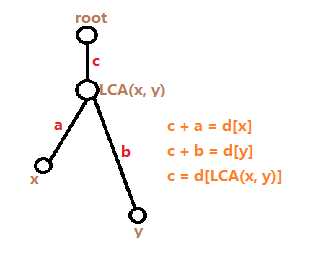
定义 $dist(x, path(a, b)) = \min_{d \in path(a, b)} dist(x, d)$ .
$dist(x, path(a, b)) = dist(x, a) + dist(x, b) - dist(a, b)$ .
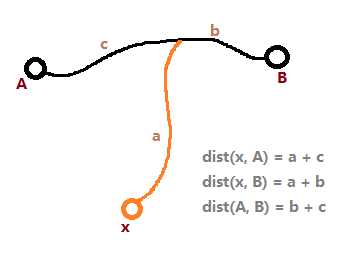
定义 $dist(path(a, b), path(c, d)) = \min_{x \in path(a, b), y \in path(c, d)} dist(x, y)$ , 不妨记 $p = LCA(a, b), q = LCA(c, d)$ .
当 $path(a, b)$ 与 $path(c, d)$ 相交时, $dist(path(a, b), path(c, d)) = 0$ .
当 $path(a, b)$ 与 $path(c, d)$ 不相交, 且 $p$ 在 $q$ 子树内时, 答案为 $dist(p, LCA(a, b))$ .
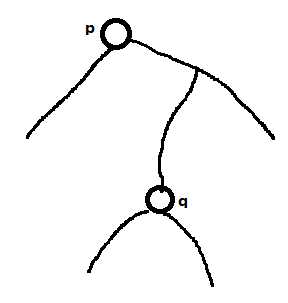
当 $path(a, b)$ 与 $path(c, d)$ 不相交, 且 $q$ 在 $p$ 子树内时, 答案为 $dist(q, LCA(c, d))$ .
否则, 答案为 $dist(p, q)$ .
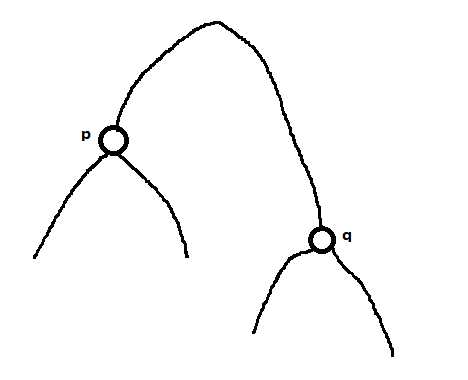
综上, 也可以表示为 $dist(path(a, b), path(c, d)) = \left\{ \begin{aligned} & 0 & , path(a, b) \cap path(c, d) \ne \emptyset \\ & \min(dist(p, LCA(c, d)), dist(q, LCA(a, b))) & , path(a, b) \cap path(c, d) \ne \emptyset \end{aligned} \right.$
标签:src 路径 http 关系 几何 lca images end 介绍
原文地址:http://www.cnblogs.com/Sdchr/p/7251758.html