标签:最大 tchar 统计学 alpha etc 速度 cos lan mit
看到题面蒟蒻忽然心塞...

题目大意:
求二维平面上质点组重心.
模拟退火是一种奇妙的搜索算法(似乎比之前的A*更恶心???)
引用一下wiki(不存在的):
模拟退火是一种通用概率算法,用来在固定时间内寻求在一个大的搜寻空间内找到的最优解。
模拟退火来自冶金学的专有名词退火。退火是将材料加热后再经特定速率冷却,目的是增大晶粒的体积,并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置,加热使能量变大,原子会离开原来位置,而随机在其他位置中移动。退火冷却时速度较慢,使得原子有较多可能可以找到内能比原先更低的位置。
模拟退火的原理也和金属退火的原理近似:我们将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
让我们小小的举个例子:
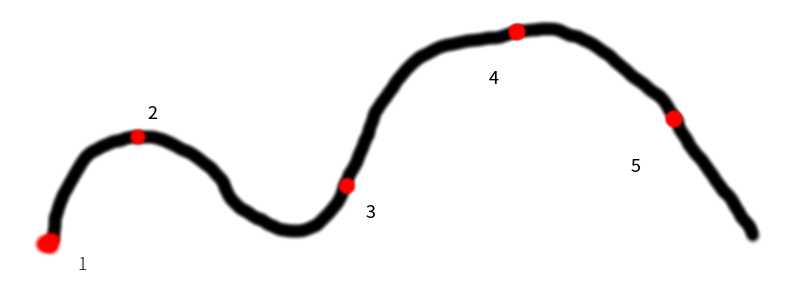
求这组数中最大的数,如果我们用贪心法,从左开始我们依次搜索1->2->3.发现3的值小于2,取得局部最优解.
然而最高点是4,mmp,看来贪心算法在此题是行不通的.
这时我们就要掏出神器:模拟退火!
事实上,模拟退火是一个脑抽+玄学的算法.比如此题中,如果我们在搜到3后,又脑抽的搜索了4,就能发现4的值比局部最优解更优.
模拟退火算法允许在合适范围内尝试选取较差解以达到整体解最优的情况.
然而,所谓的合适范围该如何选取呢?翻开万能wiki,我们找到如下说明:
- 由一个产生函数从当前解产生一个位于解空间的新解;为便于后续的计算和接受,减少算法耗时,通常选择由当前新解经过简单地变换即可产生新解的方法,如对构成新解的全部或部分元素进行置换、互换等,注意到产生新解的变换方法决定了当前新解的邻域结构,因而对冷却进度表的选取有一定的影响。
- 计算与新解所对应的目标函数差。因为目标函数差仅由变换部分产生,所以目标函数差的计算最好按增量计算。事实表明,对大多数应用而言,这是计算目标函数差的最快方法。
- 判断新解是否被接受,判断的依据是一个接受准则,最常用的接受准则是Metropolis准则:若Δt > 0则接受S′作为新的当前解S,否则以概率exp(Δt/T)接受S′作为新的当前解S。
- 当新解被确定接受时,用新解代替当前解,这只需将当前解中对应于产生新解时的变换部分予以实现,同时修正目标函数值即可。此时,当前解实现了一次迭代。可在此基础上开始下一轮试验。而当新解被判定为舍弃时,则在原当前解的基础上继续下一轮试验。
(话说Metropolis是哪位大神)
(还有对Metropolis准则我做了一些小改动,原文中Δt是前值-后值,似乎与我们(好像只是我)的认知不符)
接下来让我们解释(kou hu)一下第三点的Metropolis准则:
Δt>0时后解优于前解,此时显然优先选择后解.
Δt<0时,联系起模拟退火的内涵,我们默默掏出热力学公式:
\({P_{dE}} = {e^{\frac{{dE}}{{kT}}}}\)
P表示出现玄学解的概率.
于是核心代码如下:
1 sub = stat(now) - stat(tmp); 2 if(sub >= 0 || exp(sub / T) >= grand()) now = tmp; 3 T *= c_kappa;
然后,本题中,求解重心位置等同于找到点A,使图上的点\({P_1},{P_2},...,{P_n}\)满足\(\sum\limits_{i = 1}^n {d(a,{p_i})*{w_{{P_i}}}} \).
代码如下:
1 #include <cstdio> 2 #include <cmath> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 const int MAXS = 60 * 1024 * 32,N = 10005; 7 const double inf = 1e17;double total = inf; 8 const double c_epsilon = 1e-3; 9 const double c_kappa = 0.99; 10 const double c_pi = acos(-1); 11 char buf[MAXS]; 12 int n; 13 inline char __getchar() 14 { 15 static char buf[MAXS];static int len = 0,pos = 0; 16 if (pos == len)pos = 0,len = fread(buf,1,MAXS,stdin);if(pos == len)return EOF;return buf[pos++]; 17 } 18 inline double getdouble() 19 { 20 int num = 0,sgn = 1;char ch = __getchar();for(;ch < ‘0‘ || ch > ‘9‘;ch = __getchar())if(ch = ‘-‘)sgn = 0; 21 for(;ch >= ‘0‘ && ch <= ‘9‘;ch = __getchar())num = (num << 3) + (num << 1) + (ch ^ ‘0‘); 22 return (double) (sgn?num:(-num)); 23 } 24 struct point 25 { 26 double x,y,w; 27 point(double x_,double y_,double w_){x = x_;y = y_;w = w_;} 28 point(double x_,double y_){x = x_;y = y_;} 29 point(){} 30 void operator += (const point &a){x += a.x;y += a.y;} 31 void operator /= (const int &n){x /= n;y /= n;} 32 void operator = (const point &a){x = a.x;y = a.y;w = a.w;} 33 }p[N],ans,now; 34 inline double grand(){return (rand() % 1000 + 1) / 1000.0;} 35 inline double dist(const point &a,const point &b){return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));} 36 inline double stat(point a) 37 { 38 double res = 0.0; 39 for(int i = 1;i <= n;i++) res += dist(a,p[i]) * p[i].w; 40 if(res < total) total = res,ans = a; 41 return res; 42 } 43 void simanl() 44 { 45 double T = 100000.0,alpha,sub; 46 while(T > c_epsilon) 47 { 48 alpha = 2.0 * c_pi * grand(); 49 point tmp(now.x + T * cos(alpha),now.y + T * sin(alpha)); 50 sub = stat(now) - stat(tmp); 51 if(sub >= 0 || exp(sub / T) >= grand()) now = tmp; 52 T *= c_kappa; 53 } 54 T = c_epsilon; 55 for(int i = 1;i <= 1000;i++) 56 { 57 alpha = 2.0 * c_pi * grand(); 58 point tmp(ans.x + T * cos(alpha) * grand(),ans.y + T * sin(alpha) * grand()); 59 stat(tmp); 60 } 61 } 62 int main() 63 { 64 srand(19260817); 65 n = getdouble();for(int i = 1;i <= n;i++){double x = getdouble();double y = getdouble();double w = getdouble();p[i] = {x,y,w};now += p[i];}now /= n; 66 simanl();printf("%.3f %.3f\n",ans.x,ans.y); 67 return 0; 68 }
标签:最大 tchar 统计学 alpha etc 速度 cos lan mit
原文地址:http://www.cnblogs.com/gcc314/p/7632574.html