标签:sed 公共前缀 img 前缀 不难 不能 一段 signed display
Part1--模拟题
今天的题……怎么说呢,我觉得难度比较平均吧。就是第一题没那么简单,第三题没那么难。然后今天拿到了150分。
(1)第一题

这道题呢,其实并不难,但是容易考虑不全。
我的想法:我用last记录上一个保留数的位置(防止前一个被扔掉不能算),然后如果当前的a[i]>last && a[i]>a[i+1],即当前数比两边都大,而且a[i+2]<a[i+1](也就是后面还有递减)的话,就没戏了肯定是NO,否则last就更新为a[i],接着找。
这个想法可以说是非常奇怪了。主要是我第一次写完,觉得程序太简单了,应该不对。然后就找了几组数据,发现——果然不对。所以后面就一直在扣这几组数据:
***************
4
4 4 2 2
***************
5
1 2 5 4 3
***************
6
1 2 5 6 3 7
***************
结果最后还是WA了一个数据,因为没考虑到删除第一个。。所以这题是90分。
我的代码:

1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <algorithm> 7 using namespace std; 8 int a[1010101]; 9 int main() 10 { 11 freopen("sort.in","r",stdin); 12 freopen("sort.out","w",stdout); 13 int n; 14 scanf("%d",&n); 15 int cnt=0,last=0; 16 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 17 last=a[1]; 18 a[n+1]=9999999; 19 bool ok=true; 20 for(int i=2;i<=n;i++) 21 { 22 if(a[i]>last && a[i]>a[i+1]) 23 { 24 if(a[i+1]<=a[i+2]) {cnt++;last=a[i];i++;} 25 else cnt++; 26 } 27 else if(a[i]<last) cnt++; 28 else if(a[i]>=last) last=a[i]; 29 //cout<<i<<" "<<last<<" "<<cnt<<endl; 30 if(cnt>1) {ok=false;break;} 31 } 32 printf(ok==true? "YES":"NO"); 33 //system("pause"); 34 return 0; 35 } 36 /* 37 4 38 4 4 2 2 39 */
但是其实这种分情况讨论的思路风险挺大的,考试的时候很有可能有些点就是考虑不到。(比如去年普及组第二题……唉真是不想多说了)所以能不用就不用。这道题比较简单的正解是:求最长不下降子序列,如果这个长度>=n-1,就输出YES;否则NO。这个确实是很本质。
然而标程用的也不是最长不下降子序列...标程考虑相邻两个的大小关系。
若a[i]>a[i+1],则考虑删掉其中一个,能否变为有序
标程:

1 //std 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 int n; 8 int a[1000005]; 9 bool check(int pos){ 10 for(int i=1;i<n;i++){ 11 if(i == pos || i+1 == pos) continue; 12 if(a[i]>a[i+1]) return 0; 13 } 14 if(pos >=2 && pos<n&& a[pos-1] > a[pos+1]) return 0; 15 16 return 1; 17 } 18 int main(){ 19 freopen("sort.in","r",stdin); 20 freopen("sort.out","w",stdout); 21 scanf("%d",&n); 22 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 23 bool no = 0; 24 for(int i=1;i<n;i++){ 25 if(a[i]>a[i+1]){ 26 if( check(i) || check(i+1) ){ 27 break; 28 }else{ 29 no = 1; 30 break; 31 } 32 } 33 } 34 if(no) puts("NO"); 35 else puts("YES"); 36 37 return 0; 38 }
(2)第二题

我觉得老师出这道题纯粹就是想巩固一下昨天讲的内容吧……然而中国剩余定理太难了……所以就暴力枚举了一波。老师说枚举只能拿30,也不知道怎么拿到了60。再次证明数据比较水。。
我的代码:

1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <algorithm> 7 using namespace std; 8 9 int main() 10 { 11 freopen("mod.in","r",stdin); 12 freopen("mod.out","w",stdout); 13 int a1,b1,a2,b2,a3,b3,a4,b4; 14 scanf("%d%d%d%d%d%d%d%d",&a1,&b1,&a2,&b2,&a3,&b3,&a4,&b4); 15 long long x=1; 16 bool ok=false; 17 while(!ok) 18 { 19 if(x%a1==b1 && x%a2==b2 && x%a3==b3 && x%a4==b4) ok=true; 20 else x++; 21 } 22 printf("%d",x); 23 //system("pause"); 24 return 0; 25 }
老师的标程用的就是exgcd了。
标程:

1 //std 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <cassert> 6 #include <cmath> 7 using namespace std; 8 typedef long long LL; 9 int a[4],b[4]; 10 LL A,B; 11 LL gcd(LL a,LL b){ 12 return b==0?a:gcd(b,a%b); 13 } 14 LL lcm(LL a,LL b){ 15 return a/gcd(a,b)*b; 16 } 17 LL exgcd(LL a,LL b,LL &x,LL &y){ 18 LL t; 19 if(!b) {x=1;y=0;return a;} 20 t=exgcd(b,a%b,y,x); 21 y-=(a/b)*x; 22 return t; 23 } 24 LL mulmod(LL a,LL b,LL p){ 25 LL ret = 0; 26 while(b){ 27 if(b&1) ret=(ret+a)%p; 28 b>>=1; 29 a=(a+a)%p; 30 } 31 return ret; 32 } 33 void merge(LL a,LL b){ 34 LL k1,k2; 35 LL g = exgcd(A,-a,k1,k2); 36 LL M = lcm(A,a); 37 // assert(abs((B-b)/g*1.*k1)<=1e18); 38 k1 = mulmod((B-b)/g,k1,M); 39 // assert(abs(k1*1.*A)<=1e18); 40 LL x = B-mulmod(k1,A,M); 41 // printf("# %.3f\n",k1*1.*A); 42 // assert(x+k1*A == B); 43 // assert(x+(B-b)/g*k2*a == b); 44 // printf("# %lld %lld %lld %lld\n",x,k1,A,B); 45 assert(((x%A)+A)%A == B); 46 x = ((x%M)+M)%M; 47 assert(x%A == B); 48 assert(x%a == b); 49 A=M; 50 B=x; 51 } 52 int main(){ 53 freopen("mod.in","r",stdin); 54 freopen("mod.out","w",stdout); 55 for(int i=0;i<4;i++) scanf("%d%d",&a[i],&b[i]); 56 A=1,B=0; 57 for(int i=0;i<4;i++){ 58 merge(a[i],b[i]); 59 } 60 // printf("# %lld\n",A); 61 printf("%lld\n",B); 62 return 0; 63 }
(3)第三题

这道题……非常奇怪,一分都没得到。不知道是哪里出了问题。这道题还是暴力,都搜一遍。
我的代码:

1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <cstdio> 5 #include <cstdlib> 6 #include <algorithm> 7 using namespace std; 8 int l; 9 int minn,maxn; 10 char s[1010]; 11 int m[30]; 12 bool judge(int x,int y) 13 { 14 bool ok=true; 15 while(x<=y) 16 { 17 x++;y--; 18 if(s[x]!=s[y]) {ok=false;break;} 19 } 20 return ok==true? true:false; 21 } 22 void find(int x,int y) 23 { 24 for(int i=x;i<=y;i++) 25 { 26 m[s[i]-‘a‘+1]++; 27 if(s[i]-‘a‘+1>maxn) maxn=s[i]-‘a‘+1; 28 if(s[i]-‘a‘+1<minn) minn=s[i]-‘a‘+1; 29 } 30 } 31 bool ok() 32 { 33 for(int i=minn;i<=maxn;i++) 34 if(m[i]==m[i-1]) return true; 35 return false; 36 } 37 38 int main() 39 { 40 freopen("str.in","r",stdin); 41 freopen("str.out","w",stdout); 42 cin>>s; 43 l=strlen(s); 44 int ans=0; 45 46 for(int i=0;i<l;i++) 47 { 48 for(int j=i+3;j<l;j++) 49 { 50 if(s[i]!=s[j]) continue; 51 else 52 { 53 memset(m,0,sizeof(m)); 54 minn=9999;maxn=0; 55 if(judge(i,j)) 56 { 57 find(i,j); 58 sort(m+minn,m+maxn+1); 59 if(ok()) ans++; 60 } 61 } 62 } 63 } 64 printf("%d",ans); 65 //system("pause"); 66 return 0; 67 }
标程就比较复杂了,有用到hash。看来这道题想拿满还是不容易的
标程:

1 //std 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <map> 6 using namespace std; 7 8 typedef unsigned long long ULL; 9 typedef long long LL; 10 11 char s[10005]; 12 ULL h[10005],rh[10005],pw[10005]; 13 int L; 14 15 ULL hs(int l,int r){ 16 return h[r]-h[l-1]*pw[r-l+1]; 17 } 18 ULL rhs(int l,int r){ 19 return rh[l] - rh[r+1]*pw[r-l+1]; 20 } 21 struct N{ 22 int a[26]; 23 bool ok(){ 24 int b[26]; 25 for(int i=0;i<26;i++) b[i]=a[i]; 26 sort(b,b+26); 27 for(int i=0;i<25;i++){ 28 if(b[i]>0&& b[i] == b[i+1]) return true; 29 } 30 return false; 31 } 32 void clear(){ 33 memset(a,0,sizeof a); 34 } 35 }; 36 LL ans=0; 37 map<ULL,LL> num; 38 map<ULL,N> A; 39 void solve_odd(){ 40 for(int i=1;i<=L;i++){ 41 int l = 1,r = min(i,L-i+1)+1; 42 while(r-l>1){ 43 int mid = (l+r)/2; 44 if(hs(i-mid+1,i+mid-1)== rhs(i-mid+1,i+mid-1)) l=mid; 45 else r=mid; 46 } 47 int p=l; 48 int tmp = p; 49 while(tmp>=1&&num.find(hs(i-tmp+1,i+tmp-1))==num.end()) tmp--; 50 LL sum = 0; 51 N st; 52 st.clear(); 53 if(tmp>=1){ 54 sum=num[hs(i-tmp+1,i+tmp-1)]; 55 st = A[hs(i-tmp+1,i+tmp-1)]; 56 } 57 while(tmp<p){ 58 st.a[s[i+tmp]-‘a‘]+= (tmp == 0?1:2); 59 if(st.ok()) sum++; 60 num[hs(i-tmp,i+tmp)] = sum; 61 A[hs(i-tmp,i+tmp)] = st; 62 tmp++; 63 } 64 ans+=sum; 65 // printf("# %d %lld\n",i,sum); 66 } 67 } 68 void solve_even(){ 69 A.clear(); 70 num.clear(); 71 for(int i=1;i<L;i++){ 72 // printf("### %d\n",i); 73 int l = 1,r = min(i,L-i)+1; 74 while(r-l>1){ 75 int mid = (l+r)/2; 76 if(hs(i-mid+1,i+mid)== rhs(i-mid+1,i+mid)) l=mid; 77 else r=mid; 78 } 79 int p=l; 80 int tmp = p; 81 while(tmp>=1&&num.find(hs(i-tmp+1,i+tmp))==num.end()) tmp--; 82 LL sum = 0; 83 N st; 84 st.clear(); 85 // printf("## %d\n",p); 86 if(tmp>=1){ 87 sum=num[hs(i-tmp+1,i+tmp)]; 88 st = A[hs(i-tmp+1,i+tmp)]; 89 } 90 while(tmp<p){ 91 // printf("# %d %lld\n",tmp,sum); 92 st.a[s[i+tmp+1]-‘a‘]+= 2; 93 if(st.ok()) sum++; 94 num[hs(i-tmp,i+tmp+1)] = sum; 95 A[hs(i-tmp,i+tmp+1)] = st; 96 tmp++; 97 } 98 ans+=sum; 99 // printf("# %d %lld\n",i,sum); 100 } 101 } 102 103 int main(){ 104 freopen("str.in","r",stdin); 105 freopen("str.out","w",stdout); 106 scanf("%s",s+1); 107 L=strlen(s+1); 108 s[0]=‘#‘; 109 pw[0]=1; 110 for(int i=1;i<=L;i++) pw[i] = pw[i-1]*13131 ; 111 for(int i=1;i<=L;i++) h[i] = h[i-1]*13131 + s[i]; 112 for(int i=L;i>=1;i--) rh[i] = rh[i+1]*13131 + s[i]; 113 114 // printf("%llu %llu",hs(1,3),rhs(1,3)); 115 116 solve_odd(); 117 solve_even(); 118 printf("%lld\n",ans); 119 fclose(stdout); 120 return 0; 121 }
Part2--字符串专题
用处:快速比较两个字符串是否相等 只需O(n)
*Hash相等字符串大概率相等,Hash不等字符串一定不等
实现:RK-hash:把一个字符串看作一个base进制的大整数,然后对一个素数P取模
hash[i]=(hash[i-1]*base+s[i])%p;
【e.g】:1234500000000%p
↑
(1*10+2)%p
(12*10+3)%p
.......
【Q】:如何求任意一段hash值?
hash[l-1]*pow(base,r-l+1) 【注】:pow(x,y)=x的y次方
【Q】:求2字符串的最大公共前缀(LCP):用二分来求
【Q】:判断两字符串的大小(字典序)
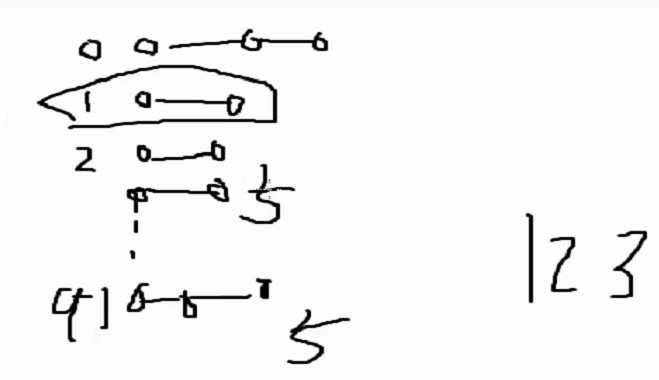
************************************************************
几个哈希需要注意的问题:
abcd != bcd
0123 --> 123
3.p一定是long long范围内的素数
如:10^18+9,23333333333333333(16个3)
************************************************************
代码实现如下:
1 //KMP poj2752 2 char t[] //模式串 3 int j=0; 4 for(int i=1;i<=n;i++) 5 { 6 while(j /*如果失配*/&& t[i]!=s[j+1]) j=nxt[j]; //尝试更短的串 7 if(y[i]==s[j+1]) j++; 8 if(j==m) //整串匹配完毕 9 { 10 j=nxt[j]; 11 } 12 }

//求最长子串 //1:暴力O(n^2) for(int i=1;i<=L;i++) { r[i]=1; whlie(s[i-r[i]]==s[i+r[i]]) r[i]++; //r[i]记录以i为中心最长能扩展出的回文串 } //2:Manacher O(n) //利用对称性,即通过已查找出的回文串(关于i对称,i+r[i]是右界)来判断当前(id为中心)是否为回文串 (将id对称到i左边) int mx=max(i+r[i]-1); int id; //mx取到最大值时的i for(int i=1;i<=L;i++) { r[i]=min(r[id-(i-id)],mx-1); //保证未出界 while(s[i-r[i]]==s[i+r[i]]) r[i]++; if(i+r[i]-1>mx) { mx=i+r[i]-1; id=i; } }
1 //扩展KMP(EXKMP),思路和manacher一样 tyvj-->1068 2 //1:暴力 3 for(int i=1;i<=n;i++) 4 { 5 p[i]=0; 6 while(b[i+p[i]]==b[p[i]+1]/*b串*/) p[i]++; 7 } 8 //2: 9 for(int i=1;i<=n;i++) 10 { 11 p[i]=min(mx-i,p[i-id]); 12 while(b[i+p[i]]==b[p[i]+1]) p[i]++; 13 if(i+p[i]>mx) 14 { 15 id=i; 16 mx=i+p[i]; 17 } 18 }
1 //Trie树:字符串排序 例题:poj2001 3630 3764(XOR最大) 2 int trie[100000][26]; 3 int tot; 4 //root=0; 5 6 void insert(char*s) 7 { 8 int p=0; 9 for(int i=0;s[i];i++) 10 { 11 if(trie[p][s[i]-‘a‘]) id=trie[p][s[i]-‘a‘]; 12 else id=trie[p][s[i]-‘a‘]=++tot; 13 } 14 flag[p]++; 15 }
AC自动机:把Trie树上不存在的孩子用它fail节点的孩子补出来
fail节点的概念与KMP的next类似
可以用一次bfs来求出
*这个就比较难了,noip的话不掌握也没关系*
标签:sed 公共前缀 img 前缀 不难 不能 一段 signed display
原文地址:http://www.cnblogs.com/lulala/p/7632834.html