标签:nts 直接 2.4 验证 程序 运算 系统 例子 1.0
1.Welcome1.java
验证结果截图:
2.Welcome2.java
验证结果截图:
3.JavaAppArguments.java
验证结果截图:
4.Addition.java
验证结果截图:
5.TestDouble.java
验证结果截图:
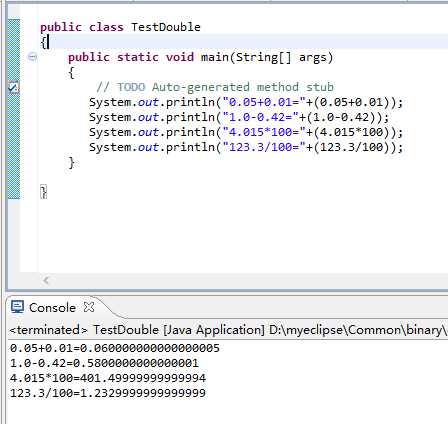
问题:为什么double类型的数值进行运算得不到“数学上精确”的结果?
十进制数的二进制表示可能不够精确
浮点数或是双精度浮点数无法精确表示的情况并不少见。浮点数值没办法用十进制来精确表示的原因要归咎于CPU表示浮点数的方法。这样的话您就可能会牺牲一些精度,有些浮点数运算也会引入误差。以上面提到的情况为例,2.4的二进制表示并非就是精确的2.4。反而最为接近的二进制表示是 2.3999999999999999。原因在于浮点数由两部分组成:指数和尾数。浮点数的值实际上是由一个特定的数学公式计算得到的。您所遇到的精度损失会在任何操作系统和编程环境中遇到。
计算机表示浮点数的方法:
s 符号位
M 表示有效数字,大于1小于2.
2^E 表示指数位。
例子:十进制的9,转化成二进制:1001.0,用二进制的科学表示法表示:1.001 * 2^3,此时s=0,
M=1.001,2^E=2^3,E= 3;
在32为的处理机中,1位表示符号位,8位表示指数位,23位表示有效数字位。我们知道科学技术法中E存在负数的情况(10 ^ -3) 所以E必须拿出一半的表示值来表示负数。
E为8位,它的取值范围为0-255;所以这个中间值就是127,他相当于0的作用。
对于上个例子 E=3 ,E+中间值=3 + 127 = 130; 130的二进制表示:10000010。有效数字计算机擦去省略第一个1的策略来存储。
6.TestBigDecimal
验证结果截图:
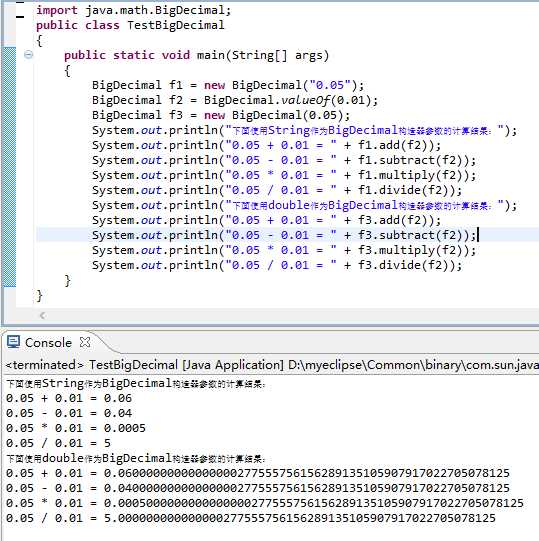
7.Verify
验证结果截图:
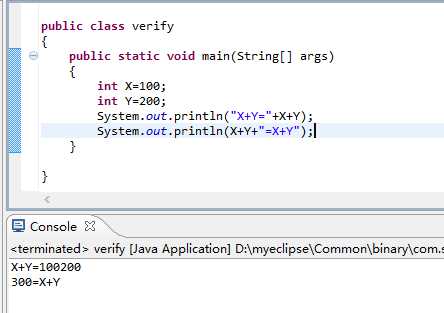
原因:
对于第一个输出,源程序直接就按部就班执行输出x,y的值,对于第二个,源程序直接将x+y计算输出,再输出要输出的结果。
标签:nts 直接 2.4 验证 程序 运算 系统 例子 1.0
原文地址:http://www.cnblogs.com/-2016/p/7634593.html