标签:合数 include print 很多 for return http 一点 它的
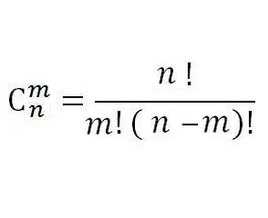
如果只是求一个组合数,当然可以直接用这个公式,用循环来实现,注意不要溢出,可以边乘边除
但是如果要求求很多个组合数呢??
一般我们用杨辉三角性质
杨辉三角上的每一个数字都等于它的左上方和右上方的和(除了边界)

第n行,第m个就是,就是C(n, m) (从0开始)
容易实现:
1 #include<cstdio> 2 const int N = 2000 + 5; 3 const int MOD = (int)1e9 + 7; 4 int comb[N][N];//comb[n][m]就是C(n,m) 5 void init(){ 6 for(int i = 0; i < N; i ++){ 7 comb[i][0] = comb[i][i] = 1; 8 for(int j = 1; j < i; j ++){ 9 comb[i][j] = comb[i-1][j] + comb[i-1][j-1]; 10 comb[i][j] %= MOD; 11 } 12 } 13 } 14 int main(){ 15 init(); 16 }
时间复杂度为O(n^2)
因为大部分题都有求余,所以我们大可利用逆元的原理(没求余的题目,其实你也可以把MOD自己开的大一点,这样一样可以用逆元做)(逆元还记得吧,前面提到的!!!)
我们需要求阶乘和逆元阶乘
我们就用1e9+7来求余吧
1 #include<cstdio> 2 const int N = 200000 + 5; 3 const int MOD = (int)1e9 + 7; 4 int F[N], Finv[N], inv[N]; //F是阶乘,Finv是逆元的阶乘 5 void init(){ 6 inv[1] = 1; 7 for(int i = 2; i < N; i ++){ 8 inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD; //求逆元 9 } 10 F[0] = Finv[0] = 1; 11 for(int i = 1; i < N; i ++){ 12 F[i] = F[i-1] * 1ll * i % MOD; 13 Finv[i] = Finv[i-1] * 1ll * inv[i] % MOD; 14 } 15 } 16 int comb(int n, int m){ //comb(n, m)就是C(n, m) 17 if(m < 0 || m > n) return 0; 18 return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD; 19 } 20 int main(){ 21 init(); 22 printf("%d\n",comb(5,2)); 23 }
看一个性质
C(n,k)=n!/(k!*(n-k)!);
C(n,k-1)=n!/((k-1)!*(n-k+1)!);
那么,C(n,k)/C(n,k-1)=(n-k+1)/k
所以C(n,k)=(n-k+1)/k*C(n,k-1);
这样,就可以从C(n,0)=1开始从左往右推,得到所有C(n,k)
不过这样还是要注意是否溢出,然后溢出的话还是要用到逆元的!!所以推荐上面那种方法。
标签:合数 include print 很多 for return http 一点 它的
原文地址:http://www.cnblogs.com/eastblue/p/7634801.html