Spark Shuffle原理、Shuffle操作问题解决和参数调优

标签：off   连接   程序   implicit   题解   随机数   解决方案   情况下   逻辑   

摘要：

   1 shuffle原理

　　1.1 mapreduce的shuffle原理

　　　　1.1.1 map task端操作

　　　　1.1.2 reduce task端操作

　　 1.2 spark现在的SortShuffleManager

    2 Shuffle操作问题解决

　　 2.1 数据倾斜原理

       2.2 数据倾斜问题发现与解决

       2.3 数据倾斜解决方案

   3 spark RDD中的shuffle算子

      3.1 去重

      3.2 聚合

      3.3 排序

      3.4 重分区

      3.5 集合操作和表操作

  4 spark shuffle参数调优

内容：

　1 shuffle原理

       概述：Shuffle描述着数据从map task输出到reduce task输入的这段过程。在分布式情况下，reduce task需要跨节点去拉取其它节点上的map task结果。这一过程将会产生网络资源消耗和内存，磁盘IO的消耗。

　　 1.1 mapreduce的shuffle原理

　　　　1.1.1 map task端操作

　　　　每个map task都有一个内存缓冲区（默认是100MB），存储着map的输出结果，当缓冲区快满的时候需要将缓冲区的数据以一个临时文件的方式存放到磁盘，当整个map task结束后再对磁盘中这个map task产生的所有临时文件做合并，生成最终的正式输出文件，然后等待reduce task来拉数据。

　　　　Spill过程：这个从内存往磁盘写数据的过程被称为Spill，中文可译为溢写。整个缓冲区有个溢写的比例spill.percent（默认是0.8），当达到阀值时map task 可以继续往剩余的memory写，同时溢写线程锁定已用memory，先对key(序列化的字节)做排序,如果client程序设置了Combiner，那么在溢写的过程中就会进行局部聚合。

　　　　Merge过程：每次溢写都会生成一个临时文件，在map task真正完成时会将这些文件归并成一个文件，这个过程叫做Merge。

　　　　1.1.2  reduce task端操作

　　　　当某台TaskTracker上的所有map task执行完成，对应节点的reduce task开始启动，简单地说，此阶段就是不断地拉取(Fetcher)每个map task所在节点的最终结果，然后不断地做merge形成reduce task的输入文件。

　　　　Copy过程：Reduce进程启动一些数据copy线程(Fetcher)通过HTTP协议拉取TaskTracker的map阶段输出文件

　　　　Merge过程：Copy过来的数据会先放入内存缓冲区（基于JVM的heap size设置），如果内存缓冲区不足也会发生map task的spill（sort 默认,combine 可选），多个溢写文件时会发生map task的merge

　　　　下面总结下mapreduce的关键词：

　　　　　　存储相关的有：内存缓冲区，默认大小，溢写阀值

　　　　　　主要过程：溢写（spill），排序，合并（combine），归并（Merge）,Copy或Fetch

　　　　　　相关参数：内存缓冲区默认大小，JVM heap size，spill.percent

　　　　　　详细

　　  1.2 spark现在的SortShuffleManager　　

SortShuffleManager运行原理

SortShuffleManager的运行机制主要分成两种，一种是普通运行机制，另一种是bypass运行机制。当shuffle read task的数量小于等于spark.shuffle.sort.bypassMergeThreshold参数的值时（默认为200），就会启用bypass机制。

普通运行机制

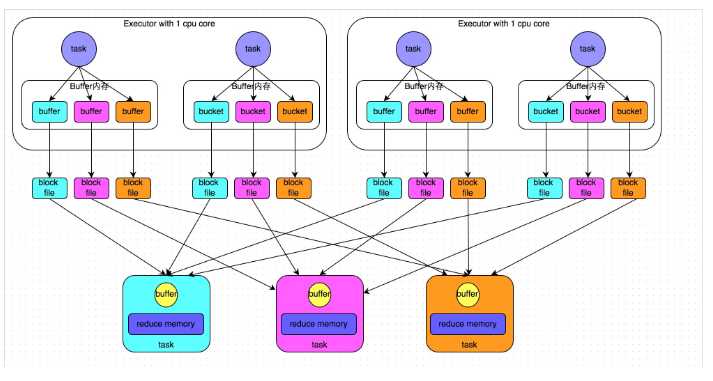
下图说明了普通的SortShuffleManager的原理。在该模式下，数据会先写入一个内存数据结构中，此时根据不同的shuffle算子，可能选用不同的数据结构。如果是reduceByKey这种聚合类的shuffle算子，那么会选用Map数据结构，一边通过Map进行聚合，一边写入内存；如果是join这种普通的shuffle算子，那么会选用Array数据结构，直接写入内存。接着，每写一条数据进入内存数据结构之后，就会判断一下，是否达到了某个临界阈值。如果达到临界阈值的话，那么就会尝试将内存数据结构中的数据溢写到磁盘，然后清空内存数据结构。

在溢写到磁盘文件之前，会先根据key对内存数据结构中已有的数据进行排序。排序过后，会分批将数据写入磁盘文件。默认的batch数量是10000条，也就是说，排序好的数据，会以每批1万条数据的形式分批写入磁盘文件。写入磁盘文件是通过Java的BufferedOutputStream实现的。BufferedOutputStream是Java的缓冲输出流，首先会将数据缓冲在内存中，当内存缓冲满溢之后再一次写入磁盘文件中，这样可以减少磁盘IO次数，提升性能。

一个task将所有数据写入内存数据结构的过程中，会发生多次磁盘溢写操作，也就会产生多个临时文件。最后会将之前所有的临时磁盘文件都进行合并，这就是merge过程，此时会将之前所有临时磁盘文件中的数据读取出来，然后依次写入最终的磁盘文件之中。此外，由于一个task就只对应一个磁盘文件，也就意味着该task为下游stage的task准备的数据都在这一个文件中，因此还会单独写一份索引文件，其中标识了下游各个task的数据在文件中的start offset与end offset。

SortShuffleManager由于有一个磁盘文件merge的过程，因此大大减少了文件数量。比如第一个stage有50个task，总共有10个Executor，每个Executor执行5个task，而第二个stage有100个task。由于每个task最终只有一个磁盘文件，因此此时每个Executor上只有5个磁盘文件，所有Executor只有50个磁盘文件。

bypass运行机制

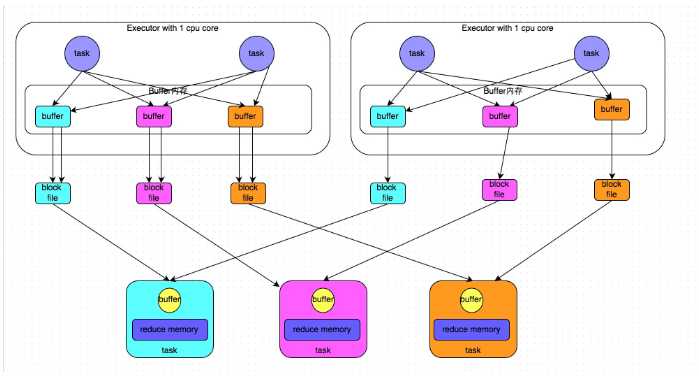
下图说明了bypass SortShuffleManager的原理。bypass运行机制的触发条件如下：

• shuffle map task数量小于spark.shuffle.sort.bypassMergeThreshold参数的值（默认为200）。
• 不是排序类的shuffle算子（比如reduceByKey）。

此时task会为每个下游task都创建一个临时磁盘文件，并将数据按key进行hash然后根据key的hash值，将key写入对应的磁盘文件之中。当然，写入磁盘文件时也是先写入内存缓冲，缓冲写满之后再溢写到磁盘文件的。最后，同样会将所有临时磁盘文件都合并成一个磁盘文件，并创建一个单独的索引文件。

该过程的磁盘写机制其实跟未经优化的HashShuffleManager是一模一样的，因为都要创建数量惊人的磁盘文件，只是在最后会做一个磁盘文件的合并而已。因此少量的最终磁盘文件，也让该机制相对未经优化的HashShuffleManager来说，shuffle read的性能会更好。

而该机制与普通SortShuffleManager运行机制的不同在于：第一，磁盘写机制不同；第二，不会进行排序。也就是说，启用该机制的最大好处在于，shuffle write过程中，不需要进行数据的排序操作，也就节省掉了这部分的性能开销。

 

    2 Shuffle操作问题解决

　　 2.1 数据倾斜原理

　　  在进行shuffle的时候，必须将各个节点上相同的key拉取到某个节点上的一个task来进行处理，此时如果某个key对应的数据量特别大的话，就会发生数据倾斜

       2.2 数据倾斜问题发现与定位

　　 通过Spark Web UI来查看当前运行的stage各个task分配的数据量，从而进一步确定是不是task分配的数据不均匀导致了数据倾斜。

       2.3 数据倾斜解决方案

　　　　2.3.1 过滤少数导致倾斜的key

　　　　2.3.2 提高shuffle操作的并行度

　　　　2.3.3 局部聚合和全局聚合

　       方案实现思路：这个方案的核心实现思路就是进行两阶段聚合。第一次是局部聚合，先给每个key都打上一个随机数，比如10以内的随机数，此时原先一样的key就变成不一样的了，比如(hello, 1) (hello, 1) (hello, 1) (hello, 1)，就会变成(1_hello, 1) (1_hello, 1) (2_hello, 1) (2_hello, 1)。接着对打上随机数后的数据，执行reduceByKey等聚合操作，进行局部聚合，那么局部聚合结果，就会变成了(1_hello, 2) (2_hello, 2)。然后将各个key的前缀给去掉，就会变成(hello,2)(hello,2)，再次进行全局聚合操作，就可以得到最终结果了，比如(hello, 4)。

　      代码：　　

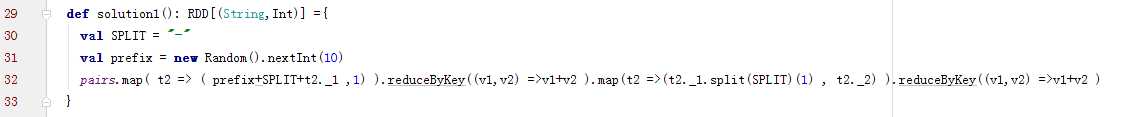
　　　　2.3.4 将reduce join转为map join（（小表几百M或者一两G））　　　　　　　　　

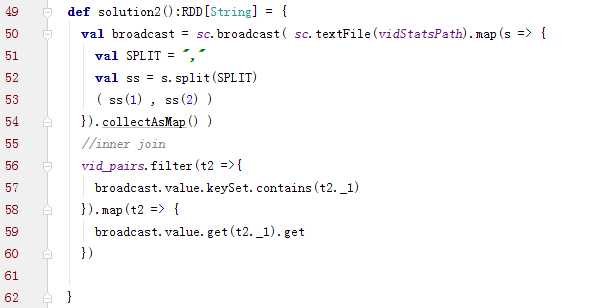
　　　　方案实现思路：不使用join算子进行连接操作，而使用Broadcast变量与map类算子实现join操作，进而完全规避掉shuffle类的操作，彻底避免数据倾斜的发生和出现。将较小RDD中的数据直接通过collect算子拉取到Driver端的内存中来，然后对其创建一个Broadcast变量；接着对另外一个RDD执行map类算子，在算子函数内，从Broadcast变量中获取较小RDD的全量数据，与当前RDD的每一条数据按照连接key进行比对，如果连接key相同的话，那么就将两个RDD的数据用你需要的方式连接起来。 　

　　 代码：

　　2.3.5 采样倾斜key并分拆join操作（join的两表都很大，但仅一个RDD的几个key的数据量过大）　　

　　

 

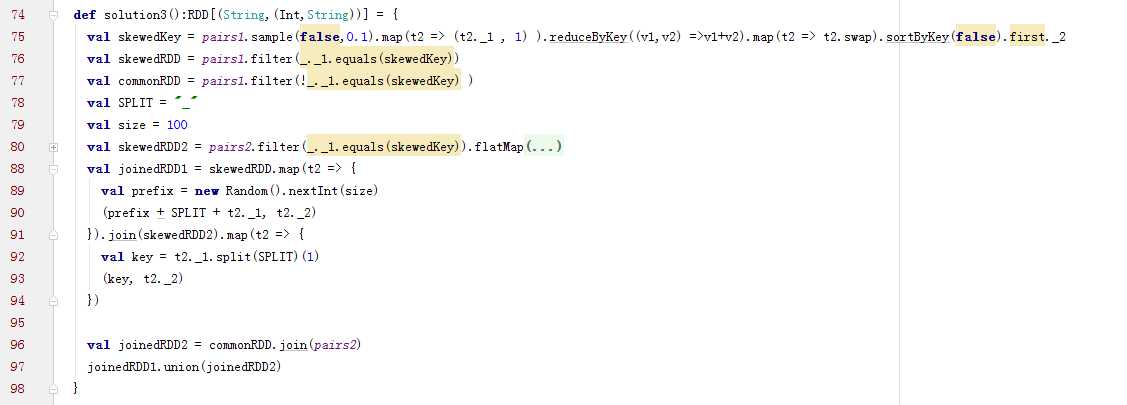
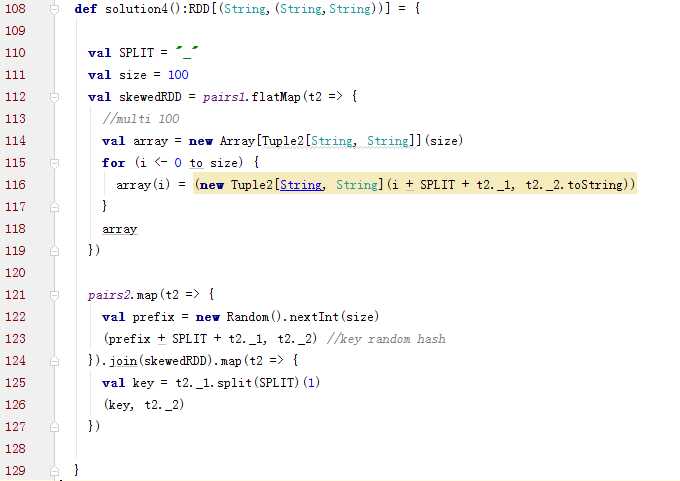
　　 2.3.6 使用随机前缀和扩容RDD进行join(RDD中有大量的key导致数据倾斜)

　　 方案实现思路：

　　 将含有较多倾斜key的RDD扩大多倍，与相对分布均匀的RDD配一个随机数。

   3 spark RDD中的shuffle算子

      3.1 去重：

　　　def distinct()

　　　def distinct(numPartitions: Int)

      3.2 聚合

　　　def reduceByKey(func: (V, V) => V, numPartitions: Int): RDD[(K, V)]

　　　def reduceByKey(partitioner: Partitioner, func: (V, V) => V): RDD[(K, V)]

　　　def groupBy[K](f: T => K, p: Partitioner):RDD[(K, Iterable[V])]

　　　def groupByKey(partitioner: Partitioner):RDD[(K, Iterable[V])]

　　　def aggregateByKey[U: ClassTag](zeroValue: U, partitioner: Partitioner): RDD[(K, U)]

　　　def aggregateByKey[U: ClassTag](zeroValue: U, numPartitions: Int): RDD[(K, U)]

　　　def combineByKey[C](createCombiner: V => C, mergeValue: (C, V) => C, mergeCombiners: (C, C) => C): RDD[(K, C)]

　　　def combineByKey[C](createCombiner: V => C, mergeValue: (C, V) => C, mergeCombiners: (C, C) => C, numPartitions: Int): RDD[(K, C)]

　　　def combineByKey[C](createCombiner: V => C, mergeValue: (C, V) => C, mergeCombiners: (C, C) => C, partitioner: Partitioner, mapSideCombine: Boolean = true, serializer: Serializer = null): RDD[(K, C)]

      3.3 排序

　　　def sortByKey(ascending: Boolean = true, numPartitions: Int = self.partitions.length): RDD[(K, V)]

 　　  def sortBy[K](f: (T) => K, ascending: Boolean = true, numPartitions: Int = this.partitions.length)(implicit ord: Ordering[K], ctag: ClassTag[K]): RDD[T]

      3.4 重分区

　　　def coalesce(numPartitions: Int, shuffle: Boolean = false, partitionCoalescer: Option[PartitionCoalescer] = Option.empty)

　　　def repartition(numPartitions: Int)(implicit ord: Ordering[T] = null)

      3.5集合或者表操作

　　　def intersection(other: RDD[T]): RDD[T]

　　　def intersection(other: RDD[T], partitioner: Partitioner)(implicit ord: Ordering[T] = null): RDD[T]

 　　  def intersection(other: RDD[T], numPartitions: Int): RDD[T]

　　　def subtract(other: RDD[T], numPartitions: Int): RDD[T]

　　　def subtract(other: RDD[T], p: Partitioner)(implicit ord: Ordering[T] = null): RDD[T]

　　　def subtractByKey[W: ClassTag](other: RDD[(K, W)]): RDD[(K, V)]

　　　def subtractByKey[W: ClassTag](other: RDD[(K, W)], numPartitions: Int): RDD[(K, V)]

　　　def subtractByKey[W: ClassTag](other: RDD[(K, W)], p: Partitioner): RDD[(K, V)]

　　　def join[W](other: RDD[(K, W)], partitioner: Partitioner): RDD[(K, (V, W))]

　　　def join[W](other: RDD[(K, W)]): RDD[(K, (V, W))]

　　　def join[W](other: RDD[(K, W)], numPartitions: Int): RDD[(K, (V, W))]

　　　def leftOuterJoin[W](other: RDD[(K, W)]): RDD[(K, (V, Option[W]))]

  4 spark shuffle参数调优　

spark.shuffle.file.buffer

• 默认值：32k
• 参数说明：该参数用于设置shuffle write task的BufferedOutputStream的buffer缓冲大小。将数据写到磁盘文件之前，会先写入buffer缓冲中，待缓冲写满之后，才会溢写到磁盘。
• 调优建议：如果作业可用的内存资源较为充足的话，可以适当增加这个参数的大小（比如64k），从而减少shuffle write过程中溢写磁盘文件的次数，也就可以减少磁盘IO次数，进而提升性能。在实践中发现，合理调节该参数，性能会有1%~5%的提升。

spark.reducer.maxSizeInFlight

• 默认值：48m
• 参数说明：该参数用于设置shuffle read task的buffer缓冲大小，而这个buffer缓冲决定了每次能够拉取多少数据。
• 调优建议：如果作业可用的内存资源较为充足的话，可以适当增加这个参数的大小（比如96m），从而减少拉取数据的次数，也就可以减少网络传输的次数，进而提升性能。在实践中发现，合理调节该参数，性能会有1%~5%的提升。

spark.shuffle.io.maxRetries

• 默认值：3
• 参数说明：shuffle read task从shuffle write task所在节点拉取属于自己的数据时，如果因为网络异常导致拉取失败，是会自动进行重试的。该参数就代表了可以重试的最大次数。如果在指定次数之内拉取还是没有成功，就可能会导致作业执行失败。
• 调优建议：对于那些包含了特别耗时的shuffle操作的作业，建议增加重试最大次数（比如60次），以避免由于JVM的full gc或者网络不稳定等因素导致的数据拉取失败。在实践中发现，对于针对超大数据量（数十亿~上百亿）的shuffle过程，调节该参数可以大幅度提升稳定性。

spark.shuffle.io.retryWait

• 默认值：5s
• 参数说明：具体解释同上，该参数代表了每次重试拉取数据的等待间隔，默认是5s。
• 调优建议：建议加大间隔时长（比如60s），以增加shuffle操作的稳定性。

spark.shuffle.memoryFraction

• 默认值：0.2
• 参数说明：该参数代表了Executor内存中，分配给shuffle read task进行聚合操作的内存比例，默认是20%。
• 调优建议：在资源参数调优中讲解过这个参数。如果内存充足，而且很少使用持久化操作，建议调高这个比例，给shuffle read的聚合操作更多内存，以避免由于内存不足导致聚合过程中频繁读写磁盘。在实践中发现，合理调节该参数可以将性能提升10%左右。

spark.shuffle.manager

• 默认值：sort
• 参数说明：该参数用于设置ShuffleManager的类型。Spark 1.5以后，有三个可选项：hash、sort和tungsten-sort。HashShuffleManager是Spark 1.2以前的默认选项，但是Spark 1.2以及之后的版本默认都是SortShuffleManager了。tungsten-sort与sort类似，但是使用了tungsten计划中的堆外内存管理机制，内存使用效率更高。
• 调优建议：由于SortShuffleManager默认会对数据进行排序，因此如果你的业务逻辑中需要该排序机制的话，则使用默认的SortShuffleManager就可以；而如果你的业务逻辑不需要对数据进行排序，那么建议参考后面的几个参数调优，通过bypass机制或优化的HashShuffleManager来避免排序操作，同时提供较好的磁盘读写性能。这里要注意的是，tungsten-sort要慎用，因为之前发现了一些相应的bug。

spark.shuffle.sort.bypassMergeThreshold

• 默认值：200
• 参数说明：当ShuffleManager为SortShuffleManager时，如果shuffle read task的数量小于这个阈值（默认是200），则shuffle write过程中不会进行排序操作，而是直接按照未经优化的HashShuffleManager的方式去写数据，但是最后会将每个task产生的所有临时磁盘文件都合并成一个文件，并会创建单独的索引文件。
• 调优建议：当你使用SortShuffleManager时，如果的确不需要排序操作，那么建议将这个参数调大一些，大于shuffle read task的数量。那么此时就会自动启用bypass机制，map-side就不会进行排序了，减少了排序的性能开销。但是这种方式下，依然会产生大量的磁盘文件，因此shuffle write性能有待提高。

spark.shuffle.consolidateFiles

• 默认值：false
• 参数说明：如果使用HashShuffleManager，该参数有效。如果设置为true，那么就会开启consolidate机制，会大幅度合并shuffle write的输出文件，对于shuffle read task数量特别多的情况下，这种方法可以极大地减少磁盘IO开销，提升性能。
• 调优建议：如果的确不需要SortShuffleManager的排序机制，那么除了使用bypass机制，还可以尝试将spark.shffle.manager参数手动指定为hash，使用HashShuffleManager，同时开启consolidate机制。在实践中尝试过，发现其性能比开启了bypass机制的SortShuffleManager要高出10%~30%。

链接：https://zhuanlan.zhihu.com/p/22024169

Spark Shuffle原理、Shuffle操作问题解决和参数调优

标签：off   连接   程序   implicit   题解   随机数   解决方案   情况下   逻辑   

原文地址：http://www.cnblogs.com/0xcafedaddy/p/7635340.html