标签:方差 表示 时间戳 频繁模式 物理 ima 覆盖 频繁模式挖掘 生成
空间轨迹是一个(x,y)点的序列,每个点都有一个时间戳.因为轨迹通常是由传感器测量的,所以它们不可避免地会出现一些错误,需要对数据进行平滑化处理。
此外,司机绕路或者交通事故也会导致轨迹数据出现偏离,这时候我们需要对轨迹数据进行异常检测。
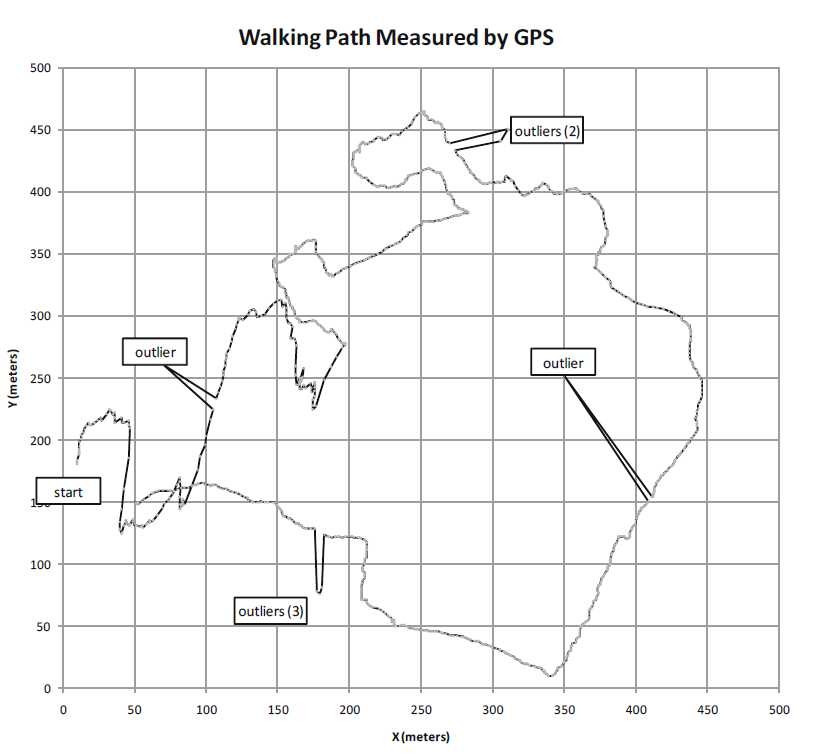
过滤技术进行为了演示,我们用一个GPS记录器记录了一个轨迹,如下图所示.在微软位于华盛顿雷德蒙的校园里,GPS 记录器以每秒1次的速度记录了1075 点.为了绘图,我们将经纬度点(x,y)转换为米.当行走本身遵循一种随意的、平滑的路径时,记录的轨迹显示由于测量噪声而出现了许多小的峰值.此外,我们还手动添加一些异常值,以模拟在记录轨迹中有时出现的大偏差.这些异常值在下图中标记出来.我们将使用这些数据来演示下面描述的过滤技术的效果.
我们用一系列坐标$x_i =(x_i,y_i)^T$来表示轨迹.i表示时间增量,$i = 1,\cdots,N$.$x_i$是一个两个元素的矢量,表示在时间为i时轨迹坐标的x和y坐标,由于传感器带来的噪声,测量并不精确.这种误差通常是通过在实际轨迹点加上未知的随机高斯噪声从而得到已知的测量到的轨迹来进行建模的,假设噪声矢量$v_i$是从具有零均值和对角协方差矩阵r的二维高斯概率密度中提取的,测量到的轨迹点坐标为矢量
\begin{equation}
z_i = x_i+ v_i
\end{equation}
\begin{equation}
v_i \sim N(0,R) \quad
R=\begin{bmatrix}
\sigma^2 & 0 \\
0 & \sigma^2
\end{bmatrix}
\end{equation}
对于GPS,上述高斯噪声模型是合理的.在我们的实验中,我们观察到标准差σ约为4米.
一种简单的方法是使用一个均值滤波器来平滑噪声.对于测量到的点$z_i$,对真正的点的估计是$z_i$及其n?1个前驱的平均值.均值滤波器可以看作是一个滑动窗口,覆盖了$z_i$ 的时间相邻值.在方程形式中,均值滤波器是
\begin{equation}
\widehat{x_i}=\frac{1}{N}\sum\limits_{j=i-n+1}^iz_j
\end{equation}
其中 $\widehat{x_i}$ 是$x_i$的估计.
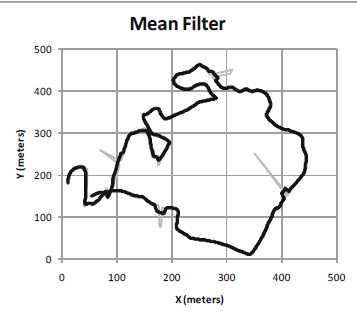
上图显示了n = 10时均值滤波器的结果,由此产生的曲线更为平滑了.
均值滤波器的一个缺点是它引入了滞后.如果真值$x_i$突然改变,均值滤波器的估计值只会逐渐响应.因此,当一个较大的滑动窗口(更大的n值)使估计值更平滑时,估计值 也会滞后于$x_i$的变化.减轻这个问题的一种方法是使用加权平均,较近的$z_i$被赋予了更多的权重.
此外,均值滤波器对离群值很敏感,解决这个问题的办法是把平均值改成中位数值(中值).中值滤波器的计算公式如下:
\begin{equation}
\widehat{x_i}=median\{z_{i-n+1}, z_{i-n+2},\cdots,z_{i-1}, z_i\}
\end{equation}
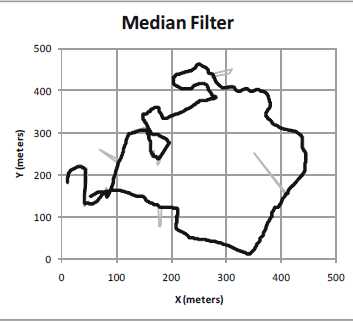
上图 显示了中值滤波器的结果,很明显它对离群值不太敏感,但仍然会得到平滑的结果.
均值滤波器和中值滤波器没有使用轨迹模型.更复杂的滤波器,如卡尔曼和粒子滤波器,可以同时模拟测量噪声(如公式(1.1))和轨迹的动力学.
卡尔曼滤波的轨迹估计是测量和运动模型之间的权衡.除了给出遵守物理定律的估计之外,卡尔曼滤波器给出了高阶运动状态(如速度)的原理性估计.
接下来我们用上面的示例轨迹介绍卡尔曼滤波器的模型.
在卡尔曼模型中,测量到的有噪声的轨迹点$z_i$可以表示为:
\begin{equation}
z_i=\begin{pmatrix}
z_i^{(x)} \\
z_i^{(y)}
\end{pmatrix}
\end{equation}
卡尔曼滤波给出了对状态向量$x_i$的估计,它描述了被跟踪的对象的完整状态.在我们的例子中,状态向量将包括对象的位置(前两行)和速度(最后两行):
\begin{equation}
x_i=\begin{pmatrix}
x_i \\
y_i \\
s_i^{(x)} \\
s_i^{(y)} \\
\end{pmatrix}
\end{equation}
$z_i$和$x_i$的关系是$z_i=H_ix_i+v_i$,其中$H_i$是在$z_i$和$x_i$中进行转换的测量矩阵,在我们的例子里,$H_i$代表我们测量$x_i$和$y_i$得到了$ z_i^{(x)}$和$ z_i^{(y)}$,但是我们没有测量速度,因此:
\begin{equation}
H_i=\begin{pmatrix}
1 &0 &0 &0 \\
0 &1 &0 &0 \\
\end{pmatrix}
\end{equation}
如果卡尔曼滤波模型的前半部分是测量,则下半部分是动态.动态模型近似于状态向量$x_i$随时间的变化,就像测量模型一样,它使用一个矩阵和附加的噪声:
\begin{equation}
x_i=\Phi_{i-1}x_{i-1}+w_{i-1}
\end{equation}
$\Phi_{i-1}$是把$x_{i-1}$和$x_i$链接起来的系统矩阵,在我们的样例中:
\begin{equation}
\Phi_i=\begin{pmatrix}
1 &0 &\Delta t_i &0 \\
0 &1 &0 &\Delta t_i \\
0 &0 &1 &0 \\
0 &0 &0 &1
\end{pmatrix}
\end{equation}
动态模型用噪声$w_{i-1}$来说明误差问题,这是另一个零均值高斯噪声项,在我们的样例中:
\begin{equation}
w_i \sim N(0,Q_i) \quad
Q_i=\begin{bmatrix}
0 &0 &0 &0 \\
0 &0 &0 &0 \\
0 &0 &\sigma_s^2 &0 \\
0 &0 &0 &\sigma_s^2
\end{bmatrix}
\end{equation}
卡尔曼滤波器除了需要一个测量模型和动态模型,它还需要假设初始状态的初始状态和不确定性.以下是所有需要的元素:
$H_i$ – 从状态$x_i$得到观测到的$z_i$的测量矩阵 \\
$R_i$ – 测量噪声协方差矩阵 \\
$\Phi_{i?1}$ – 从状态$x_{i-1}$得到观测到的${x_i}$的系统矩阵 \\
$Q_i$ – 系统噪声协方差矩阵 \\
$\widehat{x_0}$ – 初始状态估计 \\
$P_0$ – 初始状态误差协方差
最初的状态估计通常可以从第一次测量得到估计.
对于我们的例子,初始位置为$z_0$,初始速度为0.对于$P_0$,这个例子的合理估计是
\begin{equation}
P_0=\begin{bmatrix}
\sigma_s^2 &0 &0 &0 \\
0 &\sigma_s^2 &0 &0 \\
0 &0 &\sigma_s^2 &0 \\
0 &0 &0 &\sigma_s^2
\end{bmatrix}
\end{equation}
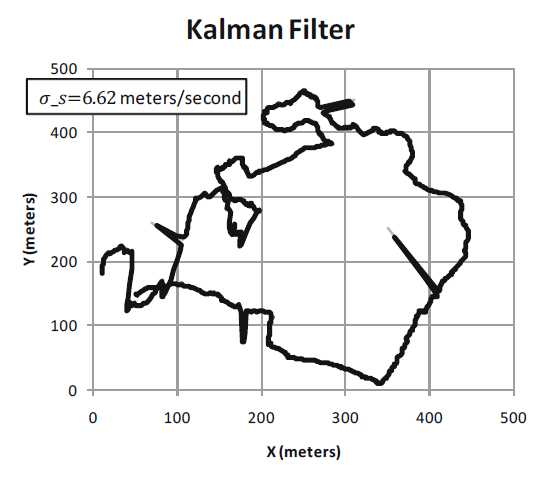
$\sigma$的值是GPS传感器噪声的估计.在我们的例子中,基于实验与先前的特定GPS记录,我们设置$σ=4$米.通过对测量到的数据中估计出速度的变化进行计算,我们设置$\sigma_s= 6.62$ 米/秒.
卡尔曼滤波器是一个两步算法,首先使用动态模型将当前状态推到下一个状态:
\begin{equation}
\begin{split}
\widehat{x}_i^{(-)}&=\Phi_{i-1}\widehat{x}_{i-1}^{(+)}\\
P_i^{(-)}&=\Phi_{i-1}P_{i-1}^{(+)}\Phi_{i-1}^T+Q_{i-1}
\end{split}
\end{equation}
第二步是将目前的测量结果纳入新的估计:
\begin{equation}
\begin{split}
K_i&=P_i^{(-)}H_i^T(H_iP_i^{(-)}H_i^T+R_i)^{-1}\\
\widehat{x}_i^{(+)}&=\widehat{x}_i^{(-)}+K_i(z_i-H_i\widehat{x}_i^{(-)})\\
P_i^{(+)}&=(I-K_iH_i)P_i^{(-)}
\end{split}
\end{equation}
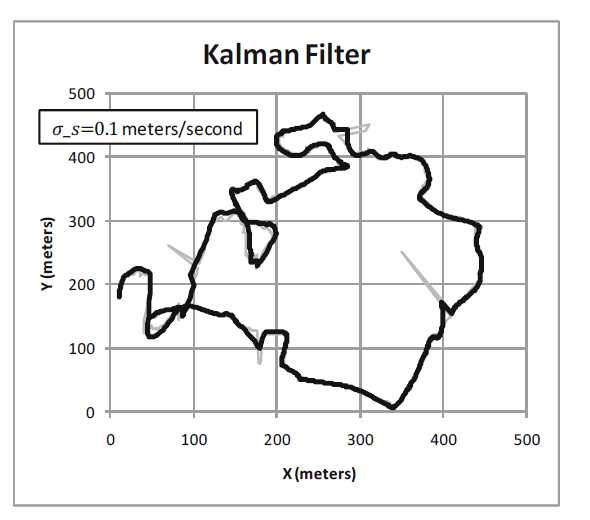
将这些方程应用于示例轨迹,可以得到下图.黑色曲线显示卡尔曼滤波器的结果.$σ_s$越小,滤波轨迹越平滑.
粒子过滤器与卡尔曼滤波器相似,它们都使用一个测量模型和一个动态模型.卡尔曼滤波器通过假设线性模型(矩阵乘法)和高斯噪声来提高效率.粒子滤波放松了这些假设得到更普遍的但是通常效率较低的算法.
粒子滤波的测量模型是概率分布$p(z_i|x_i)$,给出了给定状态向量的测量概率,对于我们的样例,我们将使用与卡尔曼滤波相同的测量模型:
\begin{equation}
p(z_i|x_i) = N((x_i, y_i)^T ,R_i)
\end{equation}
在粒子过滤器的动态模型中,我们用$p(x_{i}|x_{i-1})$取代$x_i=\Phi_{i-1}x_{i-1}+w_{i-1}$,对于我们的样例,我们将使用与卡尔曼滤波相同的动态模型,该滤波器认为位置的变化决定于速度的函数,而速度被高斯噪声随机扰动:
\begin{equation}
\begin{split}
x_{i+1}&=x_{i}+v_i^x\Delta t_i\\
y_{i+1}&=x_{i}+v_i^y\Delta t_i\\
v_{i+1}^x&=v_i^x+w_i^x \quad w_i^x \sim N(0,\sigma_s^2) \\
v_{i+1}^y&=v_i^y+w_i^y \quad w_i^x \sim N(0,\sigma_s^2)
\end{split}
\end{equation}
粒子过滤器的初始化步骤是从初始分布生成P个粒子。对于我们的例子来说,这些粒子的速度为零,并以高斯分布的方式聚集在测量到的初始位置上。我们把这些粒子称为$x^{(j)}_0$。
给定一个粒子的集合和$i>0$,第一步是重要性采样,使用动态模型$p(x_{i}|x_{i-1})$概率模拟粒子在每个时间戳上如何改变。
下一步是用测量模型计算所有粒子的权重。重要性权重$\widetilde{w}_i^j=p(z_{i}|\widetilde{x}_i^j)$.
最后一步是选择步骤$\widetilde{x_i}=\sum\limits_{j=1}^P\widetilde{w}_i^j\widetilde{x}_i^j$.
粒子过滤器的主要缺点是时间消耗。粒子数越多,效果越好,时间消耗也越大。
一个离群轨迹是在一个距离度量,例如形状和旅行时间上与语料库中其他的轨迹有明显不同的一个轨迹,或者是轨迹的一部分。这种离群轨迹可能是出租车司机的恶意绕道(Liu et al. 2014;Zhang et al. 2011)或意外的道路变化(由于交通事故或施工)。它还能提醒行驶在错误的道路上的人。一般的想法是利用现有的轨迹聚类或频繁模式挖掘方法。如果一个轨迹(或一个部分)不能在任何(基于密度的)聚类中被容纳,或者不频繁,它可能是一个异常值。Lee 等[2008] 提出了一个分区检测框架,从轨迹数据集中发现了轨迹的异常段。该方法可作为李等[2007]提出的轨迹聚类的扩展。
另一个方向是通过使用许多轨迹来检测交通异常(而不是轨迹本身)。交通异常可能是由事故、控制、抗议、运动、庆祝和其他事件引起的。Liu等人[2011]将一个城市划分为有主要道路的不连贯区域,并根据两个区域之间行驶的车辆的轨迹,收集两个区域之间的异常联系。他们将一天划分为时间仓,并确定轨迹的三个特征:轨迹里移动的车辆的数量,进入目的地区域的占所有车辆之间的比例,以及离开原区域的车辆的比例。将时间仓的三个特征分别与前几天的等效时间仓进行比较,计算每个特征的最小变形量。然后,基于时间仓的轨迹可以在一个三维空间中表示,每个维度表示一个特征的最小扭曲。后来,Mahalanobis距离用来测量极值点(在三维空间中),被认为是离群值。在上述研究之后,Chawla等[2012]提出了一个两步挖掘和优化框架,以检测两个区域之间的交通异常,并通过两个区域的交通流解释异常\end{CJK*}
标签:方差 表示 时间戳 频繁模式 物理 ima 覆盖 频繁模式挖掘 生成
原文地址:http://www.cnblogs.com/xueqiuqiu/p/7635516.html