标签:重复 pytho 四分 es2017 ase long 分类 描述 detail
盒图是在1977年由美国的统计学家约翰·图基(John Tukey)发明的。它由五个数值点组成:最小值(min),下四分位数(Q1),中位数(median),上四分位数(Q3),最大值(max)。也可以往盒图里面加入平均值(mean)。如上图。下四分位数、中位数、上四分位数组成一个“带有隔间的盒子”。上四分位数到最大值之间建立一条延伸线,这个延伸线成为“胡须(whisker)”。
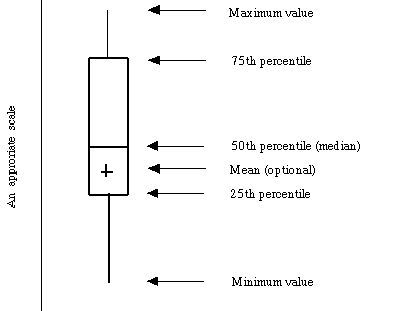
由于现实数据中总是存在各式各样地“脏数据”,也成为“离群点”,于是为了不因这些少数的离群数据导致整体特征的偏移,将这些离群点单独汇出,而盒图中的胡须的两级修改成最小观测值与最大观测值。这里有个经验,就是最大(最小)观测值设置为与四分位数值间距离为1.5个IQR(中间四分位数极差)。即:
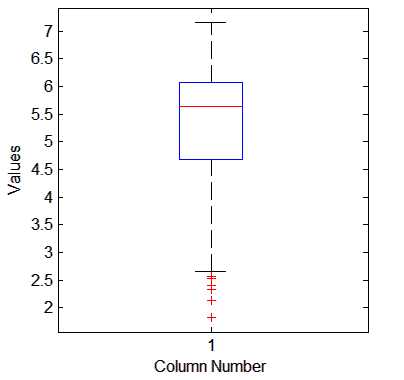
IQR = Q3-Q1,即上四分位数与下四分位数之间的差,也就是盒子的长度。
12位商学院毕业生月起薪的样本在这里按升序重复如下。
2710 2755 2850 | 2880 2880 2890 | 2920 2940 2950 | 3050 3130 3325
Q1 = 2865 Q2 = 2905(中位数) Q3 = 3000
中位数是2 905,第一个四分位数Q1 = 2865,第三个四分位数Q3 = 3000。检查这些数据,最小值为2710,最大值为3325。因此,薪水数据的五数概括数据为2710、2865、2905、3000、3325。大约1/4或25%的观察值在五数概括的相邻两个数字之间。
箱线图是在五数概括的基础上对数据进行描述的图形方法。绘制箱线图的关键是计算中位数、四分位数Q1和Q3。也可以使用四分位数全距IQR = Q3 − Q1。图1是月起薪数据的箱线图。
绘制箱线图的步骤如下:
1.画一只箱子,箱子两端分别位于第一个和第三个四分位数上。对于薪水数据来说,Q1 = 2865以及Q3 = 3000。这个箱子包括中间50%的数据。
2.在箱子中位数(薪水数据是2905)的位置画一条垂直线。
3.用四分位数全距IQR = Q3 − Q1,确定限制线的位置。箱线图的上、下限制线分别在比Q1低1.5(IQR)和比Q3高1.5(IQR)的位置上。对于薪水数据来说,IQR = Q3 − Q1 = 3000 − 2865 = 135。因此,限制线的位置在2865 − 1.5(135) = 2662.5和3000 + 1.5(135) = 3202.5处。两条限制线以外的数据可以认为是异常值。
4.图1中的虚线称为触须线。触须线从箱子两端开始绘制,直至第3步中计算的限制线内的最小值和最大值。因此,薪水数据的触须线分别在2 710和3 130处结束。
5.最后,每个异常值的位置都用星号“*”表示出来。在图1中,我们可以看到一个异常值,即3325。
在图1中,我们画出了表示上下界限位置的直线。画这些线是为了说明如何计算薪水数据的限制线并标出其位置。虽然限制线通常要计算出来,但是在箱线图中一般并不标示出来。图2显示了薪水数据的常见箱线图的形状。
import seaborn as sns sns.set_style("whitegrid") tips = sns.load_dataset("tips") # 绘制箱线图 ax = sns.boxplot(x=tips["total_bill"]) # 竖着放的箱线图,也就是将x换成y ax = sns.boxplot(y=tips["total_bill"])
Ref:
1.盒图(boxplot): http://www.blogjava.net/norvid/articles/317235.html
2. 箱线图: http://wiki.mbalib.com/wiki/%E7%AE%B1%E7%BA%BF%E5%9B%BE#_ref-1
3. Seaborn(sns)官方文档学习笔记(第五章 分类数据的绘制) https://zhuanlan.zhihu.com/p/27683042
4. python seaborn画图 : http://blog.csdn.net/suzyu12345/article/details/69029106
标签:重复 pytho 四分 es2017 ase long 分类 描述 detail
原文地址:http://www.cnblogs.com/space-place/p/7643480.html