标签:init mem code 14.3 超过 putc struct display 最快
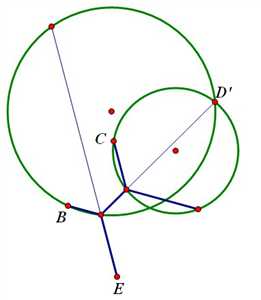
假设原来已经给定了个点,库朗等指出需要引进的点数至多为,此种点称为斯坦纳点。过每一斯坦纳点,至多有三条边通过。若为三条边,则它们两两交成120°角;若为两条边,则此斯坦纳点必为某一已给定的点,且此两条边交成的角必大于或等于120°。其中最小的网络称为已给定点的集合的最小斯坦纳树,记作SMT。若此SMT的斯坦纳点中有等于给定点的点,则称此SMT为退化的,此给定点称为退化点。
构造方法:
斯坦纳树问题是组合优化学科中的一个问题。将指定点集合中的所有点连通,且边权总和最小的生成树称为最小斯坦纳树(Minimal Steiner Tree),其实最小生成树是最小斯坦纳树的一种特殊情况。而斯坦纳树可以理解为使得指定集合中的点连通的树,但不一定最小。
可以用DP求解,dp[i][state]表示以i为根,指定集合中的点的连通状态为state的生成树的最小总权值。
转移方程有两重:
第一重,先通过连通状态的子集进行转移。
dp[i][state]=min{ dp[i][subset1]+dp[i][subset2] }
枚举子集的技巧可以用 for(sub=(state-1)&state;sub;sub=(sub-1)&state)。
第二重,在当前枚举的连通状态下,对该连通状态进行松弛操作。
dp[i][state]=min{ dp[i][state], dp[j][state]+e[i][j] }
为什么只需对该连通状态进行松弛?因为更后面的连通状态会由先前的连通状态通过第一重转移得到,所以无需对别的连通状态松弛。松弛操作用SPFA即可。
复杂度 O(n*3^k+cE*2^k)
c为SPFA复杂度中的常数,E为边的数量,但几乎达不到全部边的数量,甚至非常小。3^k来自于子集的转移sum{C(i,n)*2^i} (1<=i<=n),用二项式展开求一下和。
模版如下:
1 /* 2 * Steiner Tree:求,使得指定K个点连通的生成树的最小总权值 3 * st[i] 表示顶点i的标记值,如果i是指定集合内第m(0<=m<K)个点,则st[i]=1<<m 4 * endSt=1<<K 5 * dptree[i][state] 表示以i为根,连通状态为state的生成树值 6 */ 7 #define CLR(x,a) memset(x,a,sizeof(x)) 8 9 int dptree[N][1<<K],st[N],endSt; 10 bool vis[N][1<<K]; 11 queue<int> que; 12 13 int input() 14 { 15 /* 16 * 输入,并且返回指定集合元素个数K 17 * 因为有时候元素个数需要通过输入数据处理出来,所以单独开个输入函数。 18 */ 19 } 20 21 void initSteinerTree() 22 { 23 CLR(dptree,-1); 24 CLR(st,0); 25 for(int i=1;i<=n;i++) CLR(vis[i],0); 26 endSt=1<<input(); 27 for(int i=1;i<=n;i++) 28 dptree[i][st[i]]=0; 29 } 30 31 void update(int &a,int x) 32 { 33 a=(a>x || a==-1)? x : a; 34 } 35 36 void SPFA(int state) 37 { 38 while(!que.empty()){ 39 int u=que.front(); 40 que.pop(); 41 vis[u][state]=false; 42 for(int i=p[u];i!=-1;i=e[i].next){ 43 int v=e[i].vid; 44 if(dptree[v][st[v]|state]==-1 || 45 dptree[v][st[v]|state]>dptree[u][state]+e[i].w){ 46 47 dptree[v][st[v]|state]=dptree[u][state]+e[i].w; 48 if(st[v]|state!=state || vis[v][state]) 49 continue; //只更新当前连通状态 50 vis[v][state]=true; 51 que.push(v); 52 } 53 } 54 } 55 } 56 57 void steinerTree() 58 { 59 for(int j=1;j<endSt;j++){ 60 for(int i=1;i<=n;i++){ 61 if(st[i] && (st[i]&j)==0) continue; 62 for(int sub=(j-1)&j;sub;sub=(sub-1)&j){ 63 int x=st[i]|sub,y=st[i]|(j-sub); 64 if(dptree[i][x]!=-1 && dptree[i][y]!=-1) 65 update(dptree[i][j],dptree[i][x]+dptree[i][y]); 66 } 67 if(dptree[i][j]!=-1) 68 que.push(i),vis[i][j]=true; 69 } 70 SPFA(j); 71 } 72 }
参考09年姜碧野神牛写的论文《SPFA的优化与应用》,里面提到了一道题——[WC2008]游览计划。这题让我立刻联想到了去年北京赛区的E题,差不多的模型,大概就是在一个图中求给定的k个点的斯坦纳生成树,给定点的个数k<=10。
1 void spfa(){ 2 while(!Q.empty()){ 3 int x=Q.front()/10000,y=Q.front()%10000; 4 in[x][y]=0; 5 Q.pop(); 6 for(edge *i=Adj[x];i;i=i->nxt) //对当前节点的每条边都进行松弛操作 7 update(i->v,s[i->v]|y,d[x][y]+i->w); 8 int t=nn-1-y; 9 for(int i=t;i;i=(i-1)&t) //枚举补集的所有子集,进行松弛操作 10 update(x,y|i,d[x][y]+d[x][i|s[x]]); 11 } 12 }
这么做的复杂度是没有变的,但是常数非常大,hdu上跑了2500ms才过,仔细一想,我们发现第二松弛操作其实做了很多无用功,考虑能不能进行优化。
1 for(int y=0;y<nn;y++) //枚举连通性 2 for(int x=1;x<=n;x++){ 3 bool flag=0; 4 for(int i=(y-1)&y;i;i=(i-1)&y) //枚举所有子集,进行第一种转移 5 flag|=update(x,y,d[x][i|s[x]]+d[x][(y-i)|s[x]]); 6 if(flag) Q.push(x*10000+y); //如果节点被更新则加入队列 7 spfa(); //spfa进行第二种转移 8 }
我本来以为这样会更快一些,结果跑了4700ms = =!顿时吐槽无力。
1 for(edge *i=Adj[x];i;i=i->nxt) 2 if(update(i->v,y|s[i->v],d[x][y]+i->w)&&y==(y|s[i->v])&&!in[i->v][y]) //只把处于相同层的节点加到队列中 3 in[i->v][y]=1,Q.push(i->v*10000+y);
这样修改以后效果果然非常明显,1000ms就AC了。但还是不够快,别人最快的能够达到500ms。于是我baidu了一下,发现他们没有用spfa!大概就是把第二种转移表示成了另外一种形式:
1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #include<queue> 5 #include<algorithm> 6 #define N 60 7 #define INF 2000000 8 using namespace std; 9 struct edge{ 10 int v,w; 11 edge *nxt; 12 }E[2009],*Adj[N],*cur; 13 int n,m,K,nn; 14 int s[N],in[N][1<<10]; 15 int d[N][1<<10],dp[1<<10]; 16 queue<int> Q; 17 void addedge(int u,int v,int w){cur->v=v,cur->w=w,cur->nxt=Adj[u],Adj[u]=cur++;} 18 bool check(int x){ 19 int r=0; 20 for(int i=0;x;i++,x>>=1) 21 r+=(x&1)*(i<K?1:-1); 22 return r==0; 23 } 24 inline bool update(int x,int y,int w){ 25 if(w<d[x][y]) return d[x][y]=w,true; 26 return false; 27 } 28 void spfa(){ 29 while(!Q.empty()){ 30 int x=Q.front()/10000,y=Q.front()%10000; 31 in[x][y]=0; 32 Q.pop(); 33 for(edge *i=Adj[x];i;i=i->nxt) 34 if(update(i->v,y|s[i->v],d[x][y]+i->w)&&y==(y|s[i->v])&&!in[i->v][y]) 35 in[i->v][y]=1,Q.push(i->v*10000+y); 36 37 } 38 } 39 void init(){ 40 cur=E; 41 memset(Adj,0,sizeof(Adj)); 42 memset(s,0,sizeof(s)); 43 scanf("%d%d%d",&n,&m,&K); 44 nn=1<<(2*K); 45 for(int i=1;i<=n;i++) 46 for(int j=0;j<nn;j++) 47 d[i][j]=INF; 48 while(m--){ 49 int u,v,w; 50 scanf("%d%d%d",&u,&v,&w); 51 addedge(u,v,w); 52 addedge(v,u,w); 53 } 54 for(int i=1;i<=K;i++){ 55 s[i]=1<<(i-1),d[i][s[i]]=0; 56 s[n-i+1]=1<<(K+i-1),d[n-i+1][s[n-i+1]]=0; 57 } 58 } 59 int main(){ 60 int T; 61 scanf("%d",&T); 62 while(T--){ 63 init(); 64 for(int y=0;y<nn;y++){ 65 for(int x=1;x<=n;x++){ 66 for(int i=(y-1)&y;i;i=(i-1)&y) 67 d[x][y]=min(d[x][y],d[x][i|s[x]]+d[x][(y-i)|s[x]]); 68 if(d[x][y]<INF) Q.push(x*10000+y),in[x][y]=1; 69 } 70 spfa(); 71 } 72 for(int j=0;j<nn;j++){ 73 dp[j]=INF; 74 for(int i=1;i<=n;i++) dp[j]=min(dp[j],d[i][j]); 75 } 76 for(int i=1;i<nn;i++) 77 if(check(i)) 78 for(int j=i&(i-1);j;j=(j-1)&i) 79 if(check(j)) 80 dp[i]=min(dp[i],dp[j]+dp[i-j]); 81 if(dp[nn-1]>=INF) puts("No solution"); 82 else printf("%d\n",dp[nn-1]); 83 } 84 }
1 #include<cstdio> 2 #include<cstring> 3 #include<vector> 4 #include<queue> 5 #include<algorithm> 6 #define INF 2000000 7 #define N 10 8 using namespace std; 9 int dx[]={0,1,0,-1}, 10 dy[]={1,0,-1,0}; 11 int max_s,n,m; 12 int mat[N][N],st[N][N],vis[N][N],cnt; 13 int d[N][N][1<<N],pre[N][N][1<<N]; 14 bool in[N][N][1<<N]; 15 queue<int> Q; 16 void spfa(){ 17 int x,y,s,tx,ty,ts; 18 while(!Q.empty()){ 19 x=Q.front()/100000; 20 y=(Q.front()-x*100000)/10000; 21 s=Q.front()-x*100000-y*10000; 22 Q.pop(); 23 in[x][y][s]=0; 24 for(int i=0;i<4;i++){ 25 tx=x+dx[i],ty=y+dy[i]; 26 if(tx>=n||ty>=m||tx<0||ty<0) continue; 27 ts=s|st[tx][ty]; 28 if(d[x][y][s]+mat[tx][ty]<d[tx][ty][ts]){ 29 d[tx][ty][ts]=d[x][y][s]+mat[tx][ty]; 30 pre[tx][ty][ts]=x*100000+y*10000+s; 31 if(!in[tx][ty][ts]&&s==ts) in[tx][ty][ts]=1,Q.push(tx*100000+ty*10000+ts); 32 } 33 } 34 } 35 } 36 void go(int x,int y,int s){ 37 vis[x][y]=1; 38 int t=pre[x][y][s],tx,ty,ts; 39 if(!t) return; 40 tx=t/100000; 41 ty=(t-tx*100000)/10000; 42 ts=t-tx*100000-ty*10000; 43 go(tx,ty,ts); 44 if(x==tx&&y==ty) go(x,y,(s-ts)|st[x][y]); 45 } 46 int main(){ 47 //freopen("in.in","r",stdin); 48 scanf("%d%d",&n,&m); 49 for(int i=0;i<n;i++) 50 for(int j=0;j<m;j++){ 51 scanf("%d",&mat[i][j]); 52 if(!mat[i][j]) st[i][j]=1<<(cnt++); 53 } 54 max_s=1<<cnt; 55 for(int i=0;i<n;i++) 56 for(int j=0;j<m;j++){ 57 for(int k=0;k<max_s;k++) 58 d[i][j][k]=INF; 59 if(st[i][j]) d[i][j][st[i][j]]=0; 60 } 61 for(int k=1;k<max_s;k++){ 62 for(int i=0;i<n;i++) 63 for(int j=0;j<m;j++){ 64 if(st[i][j]&&!(st[i][j]&k)) continue; 65 for(int x=(k-1)&k;x;x=(x-1)&k){ 66 int t=d[i][j][x|st[i][j]]+d[i][j][(k-x)|st[i][j]]-mat[i][j]; 67 if(t<d[i][j][k]) d[i][j][k]=t,pre[i][j][k]=i*100000+j*10000+(x|st[i][j]); 68 } 69 if(d[i][j][k]<INF) Q.push(i*100000+j*10000+k),in[i][j][k]=1; 70 } 71 spfa(); 72 } 73 for(int i=0;i<n;i++) 74 for(int j=0;j<m;j++) 75 if(st[i][j]){ 76 printf("%d\n",d[i][j][max_s-1]); 77 go(i,j,max_s-1); 78 for(int x=0;x<n;x++){ 79 for(int y=0;y<m;y++){ 80 if(st[x][y]) putchar(‘x‘); 81 else if(vis[x][y]) putchar(‘o‘); 82 else putchar(‘_‘); 83 } 84 puts(""); 85 } 86 return 0; 87 } 88 }
1 #include<cstdio> 2 #include<cstring> 3 #include<queue> 4 #include<vector> 5 #include<algorithm> 6 #define N 209 7 using namespace std; 8 9 struct edge{int v,w;edge *nxt;}E[10009],*Adj[N],*cur; 10 int n,m,nn; 11 int d[N][1<<8],dp[1<<8]; 12 bool in[N][1<<8]; 13 int S[N],P[N],st[N],fac[4],cf,cs; 14 queue<int> Q; 15 void addedge(int u,int v,int w){cur->v=v,cur->w=w,cur->nxt=Adj[u],Adj[u]=cur++;} 16 void up(int &a,int b){if(a==-1||a>b) a=b;} 17 void spfa(){ 18 while(!Q.empty()){ 19 int x=Q.front()/1000,y=Q.front()%1000; 20 Q.pop(); 21 in[x][y]=0; 22 for(edge *i=Adj[x];i;i=i->nxt) 23 if(d[i->v][y|st[i->v]]==-1||d[x][y]+i->w<d[i->v][y|st[i->v]]){ 24 d[i->v][y|st[i->v]]=d[x][y]+i->w; 25 if(y==(y|st[i->v])&&!in[i->v][y]) in[i->v][y]=1,Q.push(i->v*1000+y); 26 } 27 } 28 } 29 bool check(int x){ 30 int t=0; 31 for(int i=0;x;i++,x>>=1) 32 t+=(x&1)*(i<cf?fac[i]:-1); 33 return t>=0; 34 } 35 int cnt(int x){ 36 int r=0; 37 for(int i=0;x;i++,x>>=1) 38 r+=(x&1)*(i<cf?0:1); 39 return r; 40 } 41 int main(){ 42 while(scanf("%d",&n)+1){ 43 cur=E; 44 cf=cs=0; 45 memset(Adj,0,sizeof(Adj)); 46 memset(st,0,sizeof(st)); 47 memset(d,-1,sizeof(d)); 48 memset(dp,-1,sizeof(dp)); 49 int ans=0; 50 for(int i=1;i<=n;i++){ 51 scanf("%d%d",P+i,S+i); 52 if(S[i]&&P[i]) P[i]--,S[i]=0,ans++; 53 if(P[i]) st[i]=1<<cf,fac[cf++]=P[i],d[i][st[i]]=0; 54 } 55 for(int i=1;i<=n;i++) 56 if(S[i]) 57 st[i]=1<<(cf+cs++),d[i][st[i]]=0; 58 nn=1<<(cf+cs); 59 60 scanf("%d",&m); 61 while(m--){ 62 int u,v,w; 63 scanf("%d%d%d",&u,&v,&w); 64 addedge(u,v,w); 65 addedge(v,u,w); 66 } 67 68 for(int y=1;y<nn;y++){ 69 for(int x=1;x<=n;x++){ 70 if(st[x]&&!(st[x]&y)) continue; 71 for(int i=(y-1)&y;i;i=(i-1)&y) 72 if(d[x][i|st[x]]!=-1&&d[x][(y-i)|st[x]]!=-1) 73 up(d[x][y],d[x][i|st[x]]+d[x][(y-i)|st[x]]); 74 if(d[x][y]!=-1) Q.push(x*1000+y),in[x][y]=1; 75 } 76 spfa(); 77 } 78 for(int i=1;i<=n;i++) 79 for(int j=0;j<nn;j++) 80 if(d[i][j]!=-1) 81 up(dp[j],d[i][j]); 82 int num=0,cost=0; 83 for(int i=1;i<nn;i++) 84 if(check(i)){ 85 for(int j=(i-1)&i;j;j=(j-1)&i) 86 if(check(j)&&check(i-j)&&dp[j]!=-1&&dp[i-j]!=-1) 87 up(dp[i],dp[j]+dp[i-j]); 88 int t=cnt(i); 89 if(dp[i]!=-1&&(t>num||(t==num&&dp[i]<cost))) 90 num=t,cost=dp[i]; 91 } 92 printf("%d %d\n",num+ans,cost); 93 } 94 }
标签:init mem code 14.3 超过 putc struct display 最快
原文地址:http://www.cnblogs.com/ECJTUACM-873284962/p/7643445.html