标签:alt mat 组合数 log 整数 prim a* sub 包含
这是一道模板题。
给定n,m,p(1\le n,m,p\le 10^51≤n,m,p≤10?5??)
求 C_{n+m}^{m}\ mod\ pC?n+m?m?? mod p
保证P为prime
C表示组合数。
一个测试点内包含多组数据。
输入格式:
第一行一个整数T(T\le 10T≤10),表示数据组数
第二行开始共T行,每行三个数n m p,意义如上
输出格式:
共T行,每行一个整数表示答案。
2
1 2 5
2 1 5
3
3
题解:求C(n,m)%p 有O(n^2)的解法,那么n,m非常大怎么办呢??
卢卡斯定理就是解决组合数取模问题的,其中p必须是质数。
首先看公式....
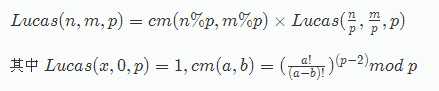
对于Lucas(n/p,m/p,p)我们递归求解,当m/p==0时返回1
对于C(n%p,m%p)这怎么办呢?a/b%p=a*x%p,其中x为b在模p
意义下的逆元。x=b^(p-2)。
代码:
#include<iostream> #include<cstdio> #include<cstring> #define maxn 200001 #define LL long long using namespace std; LL n,m,p,T; LL f[maxn]; LL ksm(LL a,LL b,LL p){ LL ret=1%p; while(b){ if(b&1)ret=ret*a%p; a=a*a%p; b>>=1; } return ret; } LL C(LL n,LL m,LL p){ if(m>n)return 0; return f[n]*ksm(f[m]*f[n-m],p-2,p)%p; } LL Lucas(LL n,LL m,LL p){ if(m==0)return 1; return (C(n%p,m%p,p)*Lucas(n/p,m/p,p))%p; } int main(){ scanf("%lld\n",&T); while(T--){ scanf("%lld%lld%lld",&n,&m,&p); f[0]=1; for(int i=1;i<=p;i++)f[i]=(f[i-1]*i)%p; printf("%lld\n",Lucas(n+m,m,p)); } }
标签:alt mat 组合数 log 整数 prim a* sub 包含
原文地址:http://www.cnblogs.com/zzyh/p/7643866.html