北极集训DAY6

 1 /*
 2     sort排序 漏了一个条件只有70 我真是 zz 
 3     对于一个合法的序列 拿走一个数插入数列中 
 4     造成的影响就是一些数向前移动 还有数向后移动 
 5     不管怎么动  向后移动或向前移动的数一定只有一个 
 6     后者都不动 
 7 */
 8 #include <algorithm>
 9 #include <cctype>
10 #include <cstdio>
11 #define N 10005000
12 int n, cnt1, cnt2, sum;
13 struct node
14 {
15     int num, pos;
16     bool operator < (node a)const
17     {
18         if(num==a.num) return pos<a.pos;
19         return num<a.num;
20     }
21 }a[N];
22 int main(int argc, char *argv[])
23 {
24     //freopen("sort.in", "r", stdin);
25     //freopen("sort.out", "w", stdout);
26     scanf("%d", &n);
27     for (int i = 1; i <= n; ++i) scanf("%d", &a[i].num), a[i].pos=i;
28     std :: sort(a + 1, a + n + 1);
29     for (int i = 1; i <= n; ++i)
30     {
31         if (a[i].pos > i) cnt1++;
32         if (a[i].pos < i) cnt2++;
33     }
34     if (cnt1 == 1 || cnt2 == 1 || (!cnt2 && !cnt1)) puts("YES");
35     else puts("NO");
36     return 0;
37     //fclose(stdin); fclose(stdout);
38 }

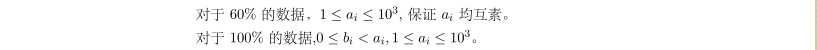
 1 /*
 2     一个模板吧 。
 3     对于60%的数据ai互质 显然可以用CRT来求解
 4     但是后40%ai不互素 CRT求解显然不对 
 5     这用了另一种方法 合并多项式 
 6     即把4个式子利用exgcd合并成1个式子
 7     即可求得ans 
 8 */
 9 #include<iostream>
10 #include<cstdio>
11 typedef long long LL; 
12 using namespace std;
13 
14 LL n,m[5],a[5];
15 LL exgcd(LL a,LL b,LL &x,LL &y)
16 {
17     if (b == 0)
18     {
19         x = 1, y = 0;
20         return a;
21     }
22     LL r = exgcd(b, a % b, x, y);
23     LL tmp = x;
24     x = y;
25     y = tmp - a / b * y;
26     return r;
27 }
28 inline LL crt()
29 {
30     LL a1 = a[1], a2, m2, d, c, m1=m[1];
31     for (LL i = 2; i <= 4; ++i)
32     {
33         a2 = a[i], m2 = m[i];
34         c = a2 - a1;
35         LL x, y;
36         d = exgcd(m1, m2, x, y);
37         x = x * c / d;
38         int mod = m2 / d;
39         x = (mod + x % mod) % mod;
40         a1 += m1 * x;
41         m1 *= mod;
42     }
43     return a1;
44 }
45 int main(int argc, char *argv[])
46 {
47     freopen("mod.in","r",stdin);
48     freopen("mod.out","w",stdout);
49     for(int i=1;i<=4;i++) cin>>m[i]>>a[i];
50     cout<<crt()<<endl;
51     return 0;
52     fclose(stdin); fclose(stdout);
53 }

  1 /*
  2     我们发现回文串是可以二分的
  3     比如：bbbabcbaabcba 我们以第1个c为
  4     中心，发现回文半径是3，大于3一定不是回文串。当回文串长度为偶数的时候
  5     我们需要特殊处理一下。
  6     现在有一个结论：本质不同的回文串个数只有O(N)个
  7     本质不同：字符串本身是不同的。
  8     每一次处理完回文串，我们要把他的hash值记录下来。
  9 */
 10 #include <cstdio>
 11 #include <cstring>
 12 #include <algorithm>
 13 #include <map>
 14 using namespace std;
 15 
 16 typedef unsigned long long ULL;
 17 typedef long long LL;
 18 
 19 char s[10005];
 20 ULL h[10005],rh[10005],pw[10005];
 21 int L;
 22 
 23 ULL hs(int l,int r){
 24     return h[r]-h[l-1]*pw[r-l+1];
 25 }
 26 
 27 ULL rhs(int l,int r){
 28     return rh[l] - rh[r+1]*pw[r-l+1];
 29 }
 30 
 31 struct N{
 32     int a[26];
 33     bool ok(){
 34         int b[26];
 35         for(int i=0;i<26;i++) b[i]=a[i];
 36         sort(b,b+26);
 37         for(int i=0;i<25;i++){
 38             if(b[i]>0&& b[i] == b[i+1]) return true;
 39         }
 40         return false;
 41     }
 42     void clear(){
 43         memset(a,0,sizeof a);
 44     }
 45 };
 46 
 47 LL ans=0;
 48 map<ULL,LL> num;
 49 map<ULL,N> A;
 50 void solve_odd(){
 51     for(int i=1;i<=L;i++){
 52         int l = 1,r = min(i,L-i+1)+1;
 53         while(r-l>1){
 54             int mid = (l+r)/2; 
 55             if(hs(i-mid+1,i+mid-1)== rhs(i-mid+1,i+mid-1)) l=mid;
 56             else r=mid;
 57         }
 58         int p=l;
 59         int tmp = p;
 60         while(tmp>=1&&num.find(hs(i-tmp+1,i+tmp-1))==num.end()) tmp--;
 61         LL sum = 0;
 62         N st;
 63         st.clear();
 64         if(tmp>=1){
 65             sum=num[hs(i-tmp+1,i+tmp-1)];
 66             st = A[hs(i-tmp+1,i+tmp-1)];
 67         }
 68         while(tmp<p){
 69             st.a[s[i+tmp]-‘a‘]+= (tmp == 0?1:2);
 70             if(st.ok()) sum++;
 71             num[hs(i-tmp,i+tmp)] = sum;
 72             A[hs(i-tmp,i+tmp)] = st;
 73             tmp++;
 74         }
 75         ans+=sum;  
 76     }
 77 }
 78 
 79 void solve_even() {
 80     A.clear();
 81     num.clear();
 82     for(int i=1;i<L;i++){
 83         int l = 1,r = min(i,L-i)+1;
 84         while(r-l>1){
 85             int mid = (l+r)/2;
 86             if(hs(i-mid+1,i+mid)== rhs(i-mid+1,i+mid)) l=mid;
 87             else r=mid;
 88         }
 89         int p=l;
 90         int tmp = p;
 91         while(tmp>=1&&num.find(hs(i-tmp+1,i+tmp))==num.end()) tmp--;
 92         LL sum = 0;
 93         N st;
 94         st.clear();
 95         if(tmp>=1){
 96             sum=num[hs(i-tmp+1,i+tmp)];
 97             st = A[hs(i-tmp+1,i+tmp)];
 98         }
 99         while(tmp<p){
100             st.a[s[i+tmp+1]-‘a‘]+= 2;
101             if(st.ok()) sum++;
102             num[hs(i-tmp,i+tmp+1)] = sum;
103             A[hs(i-tmp,i+tmp+1)] = st;
104             tmp++;
105         }
106         ans+=sum;
107     }
108 }
109 
110 int main(){
111     freopen("str.in","r",stdin);
112     freopen("str.out","w",stdout);
113     scanf("%s",s+1);
114     L=strlen(s+1);
115     s[0]=‘#‘;
116     pw[0]=1;
117     for(int i=1;i<=L;i++) pw[i] = pw[i-1]*13131 ;
118     for(int i=1;i<=L;i++) h[i] = h[i-1]*13131 + s[i];
119     for(int i=L;i>=1;i--) rh[i] = rh[i+1]*13131 + s[i];    
120     solve_odd();
121     solve_even();
122     printf("%lld\n",ans);
123     fclose(stdout);
124     return 0;
125 }