标签:表示 观察 傅里叶变换 for idt eve 复数 click 整数
FFT主要运用于快速卷积,其中一个例子就是如何将两个多项式相乘,或者高精度乘高精度的操作。
显然暴搞是$O(n^2)$的复杂度,然而FFT可以将其将为$O(n lg n)$。
这看起来十分玄学,因为怎么看它们的相乘操作都逃不过$O(n^2)$,FFT是如何再减少复杂度的呢?
讲到FFT就不可避免地出现公式,但实际上它们都是比较容易理解的。
设两个次数界均为$n$的多项式$\begin{aligned}A(x)&=a_0x^0+a_1x^1+a_2x^2+...+a_{n-1}x^{n-1}\\B(x)&=b_0x^0+b_1x^1+b_2x^2+...+b_{n-1}x^{n-1}\end{aligned}$
那么我们要求$C=A*B$。
我们把$A$、$B$和$C$的函数图像画出来,考虑每一个取值点:$C(x_1)=A(x_1)*B(x_1)$,$C(x_2)=A(x_2)*B(x_2)$,$C(x_3)=A(x_3)*B(x_3)$......
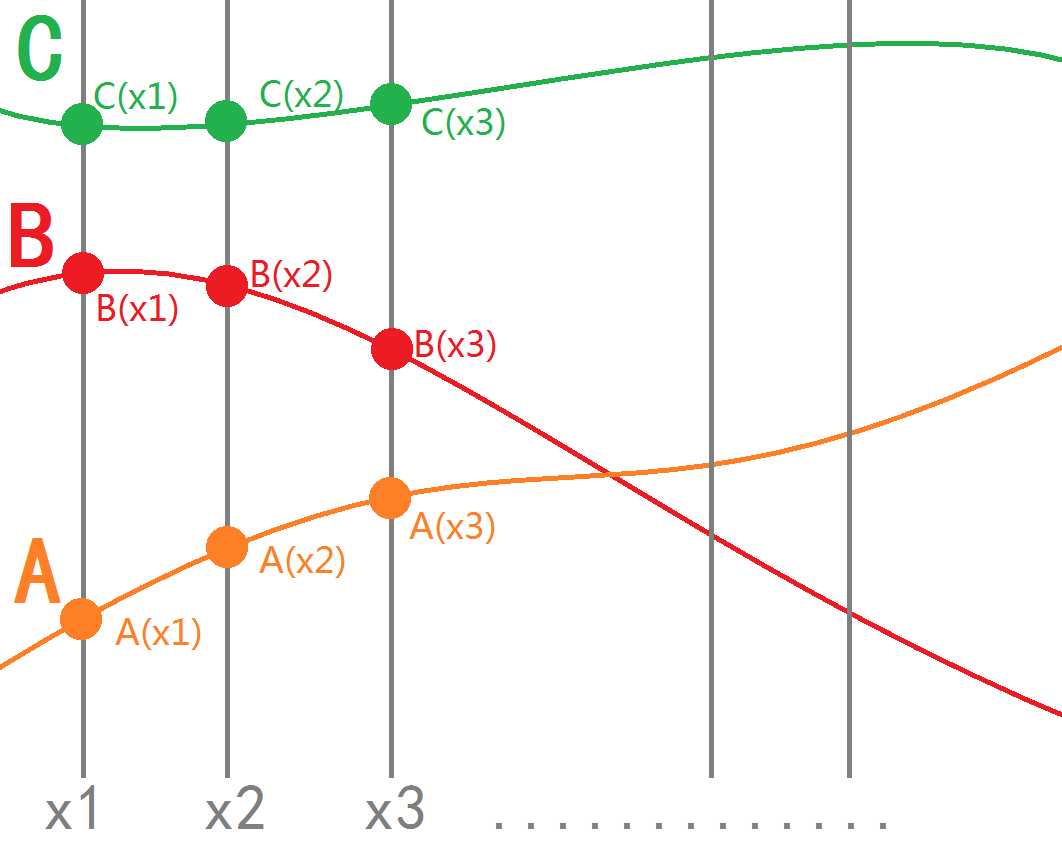
如果我们能对$A$和$B$求出它们在$x_1,x_2,...x_{2n-1}$处的值$A(x_1),A(x_2),...,A(x_{2n-1})$与$B(x_1),B(x_2),...,B(x_{2n-1})$。
那么将它们一一对应地相乘,就可以得到$C(x_1),C(x_2),...,C(x_{2n-1})$。其中,$C(x)=A(x)*B(x)$。
接着,我们可以利用$C$的这$2n-1$个点,对$C$进行插值,求出$C$的解析式。由于两个次数界为$n$的多项式相乘后是一个次数界为$2n-1$的多项式,因此我们需要$2n-1$个点,才能对$C$进行准确插值。
问题是,上面三步的时间复杂度分别为$O(n^2)$、$O(n)$和$O(n^2)$,还是没有什么改进。它们的名字分别是:DFT,点值乘法,逆DFT。
改进以后,它们分别是FFT,点值乘法,逆FFT。时间复杂度分别为$O(nlgn)$,$O(n)$,$O(nlgn)$。
本质老是没有飞跃,多半是废了,有一个因素是取值点$x_1,x_2,...,x_{2n-1}$停留在实数范围内,没有太多特殊性质。
但如果用复数呢?
定义$n$次单位复数根为满足$\omega^n=1$的复数$\omega$。$n$次单位复数根恰好有$n$个:$\omega_n^0,\omega_n^1,...,\omega_n^{n-1}$,它们的$n$次方都为1。
其中,$\omega_n^0=e^{2\pi i/n}$, $\omega_n^x=(\omega_n^0)^x$, $\omega_n^{n/2}=(e^{2\pi i/n})^{n/2}=e^{\pi i}=-1$。
(以下用$n$来代替之前提到的$2n-1$;用$A$表示一个次数界为$n$的多项式,上文提到的"$A$"和"$B$"的操作都是同理的)
我们把这$n$个$n$次单位复数根作为取值点,求出$A(\omega_n^0),A(\omega_n^1),...,A(\omega_n^{n-1})$。
这一步叫做离散傅里叶变换(DFT)。对于$k=0,1,...,n-1$,它要求$y_k=A(\omega_n^k)=\sum\limits_{j=0}^{n-1}a_j\omega_n^{kj}$
然而若不利用单位复数根的性质,复杂度仍然是$O(n^2)$的。
这$n$个复数有神秘性质,主要用到三个:
1. $\omega_n^{k+n/2}=\omega_n^k*\omega_n^{n/2}=\omega_n^k*-1=-\omega_n^k$,
什么意思呢:比如$n=8$时,$n$个单位负数根,$\omega_n^0$和$\omega_n^4$互为相反数,$\omega_n^1$和$\omega_n^5$互为相反数.....也就是$[0,n/2-1)$与$[n/2-1,n)$对应的单位复数根互为相反数。
2.消去引理:$\omega_{an}^{ak}=(e^{2\pi i/an})^{ak}=(e^{2\pi i/n})^k=\omega_n^k$,类似于分数约分。
3.折半引理:$$\begin{aligned}(\omega_n^k)^2&=\omega_n^{2k}=\omega_{n/2}^k\\(\omega_n^{k+n/2})^2=\omega_n^{2k+n}=\omega_n^{2k}*\omega_n^n&=\omega_n^{2k}=\omega_{n/2}^k\end{aligned}$$
什么意思呢?如果把$n$个单位根分成两组$\omega_n^0...\omega_n^{n/2-1}$ 和 $\omega_n^{n/2}...\omega_n^{n-1}$,两两对应位置的单位根的平方是相同的。
如$n==8$时:
$(\omega_8^0)^2=(\omega_8^4)^2=\omega_{4}^0\\(\omega_8^1)^2=(\omega_8^5)^2=\omega_{4}^1\\(\omega_8^2)^2=(\omega_8^6)^2=\omega_{4}^2\\(\omega_8^3)^2=(\omega_8^7)^2=\omega_{4}^3$
也就是$n$个$n$次单位复数根的平方的集合,等于$n/2$个$n/2$次单位复数根的集合。
我们回来看一下$A$可以如何拆分:记$A$的系数为$a_0,a_1,...,a_{n-1}$。
如果我们设$\begin{aligned}A_0(x)&=a_0x^0+a_2x^1+a_4x^2+...+a_{n-2}x^{n/2}\\A_1(x)&=a_1x^0+a_3x^1+a_5x^2+...+a_{n-1}x^{n/2}\end{aligned}$,也就是将$A$的系数奇偶分组,成为两个次数界为$n/2$的多项式。
那么有$$A(x)=A_0(x^2)+x*A_1(x^2)$$
我们求的是$A(\omega_n^0),A(\omega_n^1),...,A(\omega_n^{n-1})$,那么转换一下就变成求
$$\begin{aligned}
A(\omega_n^0)&=A_0((\omega_n^0)^2)+\omega_n^0*A_1((\omega_n^0)^2)\\
A(\omega_n^1)&=A_0((\omega_n^1)^2)+\omega_n^1*A_1((\omega_n^1)^2)\\
&...\\
A(\omega_n^{n-1})&=A_0((\omega_n^{n-1})^2)+\omega_n^{n-1}*A_1((\omega_n^{n-1})^2)\\
\end{aligned}$$
求解$A_0$和$A_1$在$n$个单位复数根,我们用递归实现。
我们发现代入$A_0$和$A_1$的参数是一个单位复数根的平方,这意味着代入$A_0$和$A_1$的单位复数根并没有$n$个。根据折半引理,代入$A_0$和$A_1$的总共只有$n/2$个不同的数:$\omega_{n/2}^0,\omega_{n/2}^1,...,\omega_{n/2}^{n/2-1}$,因为$(\omega_n^k)^2=(\omega_n^{k+n/2})^2$。
我们像上面把单位复数根分为$[0,n/2)$和$[n/2,n)$两组,观察$A(\omega_n^k)$和$A(\omega_n^{k+n/2})$,也就是相对的两个单位复数根的代入:
\begin{aligned}
A(\omega_n^k)&=A_0(\omega_{n/2}^k)+\omega_n^k*A_1(\omega_{n/2}^k)\\
A(\omega_n^{k+n/2})&=A_0(\omega_{n/2}^k)+\omega_n^{k+n/2}*A_1(\omega_{n/2}^k)\\
&=A_0(\omega_{n/2}^k)-\omega_n^k*A_1(\omega_{n/2}^k)
\end{aligned}
它们长得好像!
这下可好,我们只需要递归求解$A_0(\omega_n^0...\omega_n^{n/2-1})$和$A_1(\omega_n^0...\omega_n^{n/2-1})$,就可以求出$A(\omega_n^0...\omega_n^{n-1})$了。
时间复杂度下降的原因就在于,用$n/2$次的递归得到的数据,可以求出右半边的数值。
对于$A$和$B$都进行DFT后,我们对$n$个点值直接相乘,得到$C$的$n$个点值。
如果我们知道$C$的$n$个点值,如何知道$C$的解析式呢?
我们看一下DFT的矩阵形式:$y=V_na$,分别与下式对应:
$$\begin{bmatrix}
y_0\\y_1\\y_2\\y_3\\.\\.\\y_{n-1}
\end{bmatrix}
=
\begin{bmatrix}
1&1&1&1&...&1\\
1&\omega_n&\omega_n^2&\omega_n^3&...&\omega_n^{n-1}\\
1&\omega_n^2&\omega_n^4&\omega_n^6&...&\omega_n^{2(n-1)}\\
1&\omega_n^3&\omega_n^6&\omega_n^9&...&\omega_n^{3(n-1)}\\
...&...&...&...&...&...\\
1&\omega_n^{n-1}&\omega_n^{2(n-1)}&\omega_n^{3(n-1)}&...&\omega_n^{(n-1)(n-1)}
\end{bmatrix}
*
\begin{bmatrix}
a_0\\a_1\\a_2\\a_3\\.\\.\\a_{n-1}
\end{bmatrix}$$
我们所求的是$a$,而$a=yV_n^{-1}$,求出$V_n$的逆矩阵即万事大吉了。
定理:对于$V_n$,$(k,j)$处的元素为$\omega_n^{kj}$。
而对于$V_n^{-1}$,$(k,j)$处的元素为$\omega_n^{-kj}/n$。
如果想简单证明的话,将$V_n^{-1}$写出来算一算就好。(可以参见算导)
那么$a_j=\frac{1}{n}\sum\limits_{k=0}^{n-1}y_k\omega_n^{-kj}$。
看回上面DFT的算式表达,我们发现它们长得几乎一样:IFFT的表达,仅仅是多了一个$\frac{1}{n}$,以及单位复数根的指数取负数。
这就非常棒了:IFFT的程序其实和FFT一样,只不过单位复数根替换一下,算完以后,每一个数值都除去$n$即可,具体参见代码解释。
FFT的应用,主要是将问题转化成如DFT式子的形式,用FFT来进行加速或计算的操作。
附上递归版代码和非递归版代码:

#include <cstdio> #include <vector> #include <cmath> #define max(a,b) ((a)>(b)?(a):(b)) using namespace std; const int N=50010; const double Pi=3.14159265358979323846; struct Comp{//手写了一个复数类 double a,b; Comp(){a=b=0.0;} Comp(double x,double y){a=x;b=y;} friend Comp operator + (Comp x,Comp y){ return Comp(x.a+y.a,x.b+y.b); } friend Comp operator - (Comp x,Comp y){ return Comp(x.a-y.a,x.b-y.b); } friend Comp operator * (Comp x,Comp y){ return Comp(x.a*y.a-x.b*y.b,x.b*y.a+x.a*y.b); } }; typedef vector<Comp> vc; int A,B,type,len; vc a,b,c; vc fft(vc u,int flag){//flag标识是否为逆FFT int n=u.size(); if(n==1) return u;//规模为1时,只有一个常数项的多项式的FFT就为这个常数,可以直接返回了 Comp w_n=Comp(cos(2*Pi/n),sin(2*Pi/n)),w=Comp(1,0);//算出单位复数根的底w_n;w是用来迭代的,减少计算次数 if(flag) w_n.b*=-1.0;//逆FFT与FFT的不同 vc a0,a1,v; a0.clear(); a1.clear(); v.clear(); for(int i=0;i<n;i++){//系数按奇偶分组 if(i&1) a1.push_back(u[i]); else a0.push_back(u[i]); v.push_back(Comp(0,0)); } //递归求解A0和A1 a0=fft(a0,flag); a1=fft(a1,flag); //用一半的数据,综合算出全部的结果,w在此处不断乘上w_n,就保证它是w_n的k次方 for(int k=0;k<=n/2-1;k++){ v[k]=a0[k]+w*a1[k]; v[k+n/2]=a0[k]-w*a1[k]; w=w*w_n; } return v; } int main(){ //原题:求两个多项式相乘后的系数(系数都为整数) scanf("%d%d%d",&A,&B,&type); A++; B++; for(int i=0,x;i<A;i++) scanf("%d",&x),a.push_back(Comp(x,0)); for(int i=0,x;i<B;i++) scanf("%d",&x),b.push_back(Comp(x,0)); len=1;//算出高位补齐len(上文提到的至少需要2n-1个点),并把两个多项式的次数都扩展到len //代码里的len指的是上文提到的n while(len<(max(A,B)*2)) len<<=1; for(int i=A;i<len;i++) a.push_back(Comp(0,0)); for(int i=B;i<len;i++) b.push_back(Comp(0,0)); //求两个多项式在n个单位复数根的值O(nlgn) a=fft(a,0); b=fft(b,0); //点值乘法 O(n) for(int i=0;i<len;i++) c.push_back(a[i]*b[i]); //对点值乘法的结果进行逆FFT O(nlgn) c=fft(c,1); for(int i=0;i<A+B-1;i++) printf("%d ",(int)(c[i].a/len+0.5));//除去len,四舍五入(这题是整数) return 0; }

#include <cstdio> #include <iostream> #include <cmath> #define max(a,b) ((a)>(b)?(a):(b)) using namespace std; const int N=50010; const double Pi=3.14159265358979323846; struct Comp{ double a,b; Comp(){a=b=0.0;} Comp(double x,double y){a=x;b=y;} friend Comp operator + (Comp x,Comp y){return Comp(x.a+y.a,x.b+y.b);} friend Comp operator - (Comp x,Comp y){return Comp(x.a-y.a,x.b-y.b);} friend Comp operator * (Comp x,Comp y){return Comp(x.a*y.a-x.b*y.b,x.b*y.a+x.a*y.b);} }a[N*4],b[N*4]; int A,B,type,n; inline int rev(int x){ int ret=0; for(int i=1;i<n;i<<=1,x>>=1) ret=(ret<<1|(x&1)); return ret; } void fft(Comp *a,int f){ int lg=log2(n),len; Comp w,w_n,u,v; for(int i=0,t;i<n;i++) if(i<(t=rev(i))) swap(a[i],a[t]); for(int i=1;i<=lg;i++){ len=1<<i; w_n=Comp(cos(2*Pi/len),sin(2*Pi/len)*f); for(int j=0;j<n;j+=len){ w=Comp(1,0); for(int k=0;k<=len/2-1;k++){ u=a[j+k]; v=w*a[j+k+len/2]; a[j+k]=u+v; a[j+k+len/2]=u-v; w=w*w_n; } } } } int main(){ scanf("%d%d%d",&A,&B,&type); for(int i=0,x;i<A;i++) scanf("%lf",&a[i].a); for(int i=0,x;i<B;i++) scanf("%lf",&b[i].a); for(n=1;n<A+B;n<<=1); fft(a,1); fft(b,1); for(int i=0;i<n;i++) a[i]=a[i]*b[i]; fft(a,-1); for(int i=0;i<A+B-1;i++) printf("%d\n",(int)(a[i].a/n+0.5)); return 0; }
标签:表示 观察 傅里叶变换 for idt eve 复数 click 整数
原文地址:http://www.cnblogs.com/RogerDTZ/p/7444267.html