标签:cal 运算符 挑战 += 后缀表达式 保存 代码 需求分析 ror
1 项目 GitHub 地址
GitHub地址:https://github.com/huzhiquan/sizeyunsuan
2 PSP
|
PSP |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planing |
计划 |
10 |
10 |
|
Estimate |
估计这个任务需要多少时间 |
10 |
10 |
|
Development |
开发 |
700 |
900 |
|
Analysis |
需求分析(包括学习新技术) |
40 |
70 |
|
Design Spec |
生成设计文档 |
30 |
30 |
|
Design Review |
设计复审 (和同事审核设计文档) |
10 |
10 |
|
Coding Standard |
代码规范 (为目前的开发制定合适的规范) |
20 |
10 |
|
Design |
具体设计 |
30 |
50 |
|
Coding |
具体编码 |
500 |
600 |
|
Coding Review |
代码复审 |
60 |
90 |
|
Test |
测试(自我测试,修改代码,提交修改) |
60 |
90 |
|
Reporting |
报告 |
120 |
180 |
|
Test Report |
测试报告 |
60 |
150 |
|
Size Measurement |
计算工作量 |
10 |
10 |
|
Postmortem & Process Improvement Plan |
事后总结, 并提出过程改进计划 |
30 |
30 |
|
合计 |
|
850 |
1490 |
3 项目要求
1、 参与运算的操作数(operands)除了100以内的整数以外,还要支持真分数的四则运算。操作数必须随机生成。
2、 运算符(operators)为 +, ?, ×, ÷ 运算符的种类和顺序必须随机生成。
3、 要求能处理用户的输入,并判断对错,打分统计正确率。
4、 使用 -n 参数控制生成题目的个数。
附加要求
1、 支持带括号的多元复合运算
2、 运算符个数随机生成(考虑小学生运算复杂度,范围在2~10)
4 解题思路
先不考虑附加要求的话,本题可以简化为100以内的整数和真分数的四则运算,运算符个数定为3个,真分数,整数,操作符均随机生成。等完成基本要求,再考虑附加要求比较好。
对于本题,首先要考虑的是以什么结构去存储真分数,运算简单,不容易出错。本项目的思想是将真分数用String保存,在运算时,将string形式的分数中的分子分母以/为界,保存到二维数组中,分开运算。运算的时候,要注意分子分母为0等的特殊情况。
然后要考虑的是在随机生成的整个表达式中,乘法和除法要优先计算,这里暂不考虑带括号的表达式。因此将表达式转换为后缀表达式再计算结果,这之中用到了栈,容易出现栈溢出的问题,需要考虑。
最后将结果用字符串表示,并与用户输入的进行比较,判断对错。
5 代码说明
1、 随机生成真分数,操作符和整数
//生成真分数
public static int[] generateFraction()
{
int [] fraction=new int[2];
int temp=0;
int x,y;
x=new Random().nextInt(99)+1;
y=new Random().nextInt(99)+1;
while(x==y)
{
y=new Random().nextInt(99)+1;
};
if(x>y)
{
temp=x;
x=y;
y=temp;
}
fraction[0]=x;
fraction[1]=y;
return fraction;
}
//生成操作符
public static String generateOperater()
{
String[] Operater={"+","-","×","÷"};
int x=new Random().nextInt(4);
String Op=Operater[x];
return Op;
}
//生成数
//生成整数或随机数本身也是随机的
public static String generateNum()
{
int x=new Random().nextInt(2);
if(x==0)
{
int y=new Random().nextInt(100);
return String.valueOf(y);
}
else {
int []y=generateFraction();
return String.valueOf(y[0])+"/"+String.valueOf(y[1]);
}
}
1、 加法计算
//计算加法
public static String add(String a,String b){
if((a.contains("/")==false)&&(b.contains("/")==false)){
int intofa=Integer.valueOf(a);
int intofb=Integer.valueOf(b);
return String.valueOf(intofa+intofb);
}
else if((a.contains("/")==true)&&(b.contains("/")==false))
{
int []result = new int[2];
int []fractionofa=strToarr(a);
int intofb=Integer.valueOf(b);
//分母化同并实现运算
result[0]=fractionofa[0]+fractionofa[1]*intofb;
result[1]=fractionofa[1];
return simplify(result);
}
else if((a.contains("/")==false)&&(b.contains("/")==true))
{
int []result = new int[2];
int intofa=Integer.valueOf(a);
int []fractionofb=strToarr(b);
//分母化同并实现运算
result[0]=intofa*fractionofb[1]+fractionofb[0];
result[1]=fractionofb[1];
return simplify(result);
}
else{
int []result =new int[2];
int []fractionofa=strToarr(a);
int []fractionofb=strToarr(b);
//分母化同并实现运算
result[0]=fractionofa[0]*fractionofb[1]+fractionofa[1]*fractionofb[0];
result[1]=fractionofa[1]*fractionofb[1];
return simplify(result);
}
}
2、 中缀表达式转换为后缀表达式
//由中缀转换为后缀
private String infixTopost()
{
String[] strArr=getInfix(input).split(" ");
for (int i = 0; i < strArr.length; i++) {
String x=strArr[i];
switch(x){
//当x为符号时,与当前栈顶的符号比优先级,若x的优先级≤栈顶元素,则将栈顶元素出栈,再将x入栈
case "+":
case "-":transfer(x,1);break;
case "×":
case "÷":transfer(x,2);break;
//当x为数字时,直接加到post中
default:post+=" "+x;break;
}
}
while (stack.isEmpty()==false) {//将栈中最后一个元素出栈
post += " " + stack.pop();
}
post=post.trim();//去掉第一个空格
//System.out.println("后缀表达式:"+post);
return post;
}
//当x为符号时,与当前栈顶的符号比优先级,若x的优先级≤栈顶元素,则将栈顶元素出栈,再将x入栈
private void transfer(String x,int priority)
{
while(stack.isEmpty()==false){
String top=stack.pop();
int priorityoftop=getpriority(top);
if(priority>=priorityoftop)//当x的优先级>=栈顶元素优先级时
{
stack.push(top);
break;
}
else{//当x的优先级<栈顶元素优先级时
post+=" "+top;
}
}
stack.push(x);
}
//判断操作符的优先级
private int getpriority(String top) {
// TODO Auto-generated method stub
if(top.equals("+")==true||top.equals("-")==true)
{
return 1;
}
else return 2;
}
4、计算后缀表达式
private String infixTopost()
{
String[] strArr=getInfix(input).split(" ");
for (int i = 0; i < strArr.length; i++) {
String x=strArr[i];
switch(x){
//当x为符号时,与当前栈顶的符号比优先级,若x的优先级≤栈顶元素,则将栈顶元素出栈,再将x入栈
case "+":
case "-":transfer(x,1);break;
case "×":
case "÷":transfer(x,2);break;
//当x为数字时,直接加到post中
default:post+=" "+x;break;
}
}
while (stack.isEmpty()==false) {//将栈中最后一个元素出栈
post += " " + stack.pop();
}
post=post.trim();//去掉第一个空格
//System.out.println("后缀表达式:"+post);
return post;
}
5、计算算式结果
//由后缀表达式得结果
public String postToresult()
{
String[] strArr=infixTopost().split(" ");
for(int i = 0; i < strArr.length; i++){
String temp = strArr[i];
if(isOperater(temp)==false){//是数字时,入栈
stack.push(temp);
}else{//是操作符时,将栈顶两个元素进行运算,结果入栈
stack.push(compute1(temp));
}
}
return stack.pop();
}
//四则运算
private static String STACK_ERROR="THE STACK IS NULL!";
private String compute1(String temp) {
// TODO Auto-generated method stub
compute com=new compute();
String result = "";
String a;
String b;
while(true){
if(stack==null||stack.size()==0){return "栈为空a1";}
String tempa=stack.pop();
if(tempa.equals(STACK_ERROR)){return "栈为空a2";}
if(!tempa.equals("")){a=tempa;break;}
}
while(true){
if(stack==null||stack.size()==0){return "栈为空b1";}
String tempb=stack.pop();
if(tempb.equals(STACK_ERROR)){return "栈为空b2";}
if(!tempb.equals("")){b=tempb;break;}
}
switch(temp)
{
case "+":
result=com.calculate(b, a, "+");
//System.out.println("test:"+b+"+"+a+"="+ result);
break;
case "-":
result=com.calculate(b, a, "-");
//System.out.println("test:"+b+"-"+a+"="+ result);
break;
case "×":
result=com.calculate(b, a, "×");
//System.out.println("test:"+b+"×"+a+"="+ result);
break;
case "÷":
if(a.equals("0")){return "被除数为0";};
result=com.calculate(b, a, "÷");
//System.out.println("test:"+b+"÷"+a+"="+ result);
break;
default:break;
}
return result;
}
6 测试运行
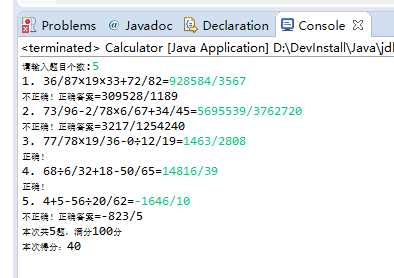
7个人小结
本次项目对于我来说是个不小的挑战,且项目本身还存在很多瑕疵:不支持带括号的多元复合运算,运算符的个数不能随机生成,且在生成很多算式的时候,运行会变慢等等。还有很多需要优化的地方,由此经历我也更明白自己的薄弱点在哪里,在未来的学习中,我会继续提升自己,克服短板。
标签:cal 运算符 挑战 += 后缀表达式 保存 代码 需求分析 ror
原文地址:http://www.cnblogs.com/cswhu-huzhiquan/p/7653156.html