近一段时间以来笔者一直在查找关于受限玻尔兹曼机(Restricted Boltzmann Machine,下简称RBM)的相关资料,其实CSDN上的相关帖子已经其二值分布的情况介绍的比较到位,而且在《机器学习》(于剑著)也以较短的篇幅描述了此类神经网络的相关情况,但不知为什么此书的符号有点奇怪(在推导中涉及到显层和隐层的偏置不是用很明显的方式来表达的),而且似乎只推导到相关边缘分布,感觉让人意犹未尽。
但是关于RBM的非二值情况(主要是实数,其模型源于高斯分布)在网络上总是无法查找到,幸而最近我在一个帖子中看到了相关内容,但没有任何推导过程,只有结论。文中说这是Hinton教授一篇论文中所提到的,但我也没有找到此论文的内容,不过根据最终的结论我给出了一个可能的推导,仅以本文记录之。
不过在展开相关推导之前,还是想将RBM的相关基础内容介绍一二,主要包括基于二值逻辑的RBM以作为预备知识和必要的铺垫。
另外,多说句闲话,这个RBM到底有什么作用?其实它是一种无监督的训练模型,一般可以作为编码压缩(你可以认为这是一种PCA方法)或作为其它有监督训练的预热模型,以免在网络初始训练阶段,各个需求的参数初值不靠谱而造成训练时间过长。
所谓RBM,就我个人理解而言,其实就是建立在玻尔兹曼能量分布概率模型上的一个随机系统,而RBM的网络结构我也不费力解释,这在各类文档中有大量的阐述,总体而言它是一个含有m个显层节点和n个隐层节点的网络,而显层和隐层之间是全连接的,但显层和隐层内部的各个节点之间无任何联系,所以它也是一个二部图。
对于受限玻尔兹曼的能量的定义如下:
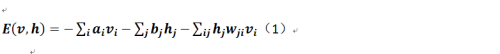
这个公式其实不用过多解释,其中v和h分别表示显层和隐层,而a和b分别表示显层和隐层的偏置,w(有两个下标)则表示显层节点和隐层节点之间连接的权重,很明显它是一个m*n的矩阵。那么在机器学习的范畴中是如何描述玻尔兹曼分布的?
即其实Z是一个所谓的归一化因子,它的结果就是整个网络的能量之和(就是全部样本的Power!因为有隐层的存在,所以这个值其实好难求,这就是为什么需要使用GIBBS抽样或对比散度抽样来逼近这个)。
另外,为了下面推导方便引入一个记号:
我们讨论的是非二值情况的RBM推导过程,但是为了统一起见先推导下二值分布的RBM。
任何机器学习问题,我们可能都会导向一个对目标函数最优值的求解问题,这个RBM也没有任何例外,这目标函数为一个以对数形式表达的似然函数:
但我们在后面可以看到,对于RBM而言其边缘分布及条件分布都是极难获得的!上式中![]() 表示每个样本。
表示每个样本。
下面给出基于单个样本v(被标识为红色,而黑色的v则表示所有样本,下同)的似然公式:
为了推导方便,现仅针对单个样本的似然函数进行推导,多个样本只是最终的一个样本之和。
那么我们对公式(6)各个参数求偏导(按照惯例希腊字母θ表示各个待定的参数,即a、b和w),可以得到:
进而,对于各个参数的梯度而言,可以得到如下公式(其中过程中出现的各类繁琐的推导就不再给出,可以参照CSDN的相关文档,作者是皮果提,他给出的过程其实已经足够详细):
对于连接权重的偏导数:
那么对于多个样本而言相关公式又改是如何呢?现在假定我们有N个样本(这个要和显层、隐层的神经元数量进行区分),可得:
N个样本连接权重的偏导数之和:
至此我们已经把N个样本的相关各个参数的偏导形式求了出来!且慢,我们对于各个条件概率该如何求出(即对于公式7的第一部分该如何求解?第二部分该怎么弄?那个只能求助于GIBBS或对比散度采样),下面给出:
公式7的第一部分的直观感觉是在显层已知(这个是费话,因为在初始情况下v就是样本,当然已知)的情况下,怎么得到隐层的条件分布?这个推导是这样的(笔者把参考的相关文档倒过来进行分析,而且需注意这个是对一个样本而言的,不是多个!):
那么类似的,在隐层已知的情况下显层相关神经元的值取1的条件概率是:
最后可将公式14、15分别带入之前的相关推导结果就能得到完整的二值型受限玻尔兹曼机的公式。
经过笔者一段时间的思考,为什么网上介绍RBM基本上都是基于二值的(这个好像没什么用,因为至少我要用256级灰度的图像来学习,这个只能归一化到(0,1)区间,难道要把神经元数量再乘以256,那么对于MINST库来说岂不是显层的神经元有28*28*256个)?可能是此类网络最后的推导结果正好可以使用sigmoid来表示吧?还是由于二值的逻辑非常简单?但其实本文中的证明过程已经省略了很多,比如公式14中第4行是怎么来的?就是把它们再用能量的方式表示出来,将除法运算转化为指数的减法运算而已(减去公共项)。
受限玻尔兹曼机的推导过程其实已经最够复杂,但还好只是繁琐而并不困难,关键点在于贝叶斯公式的使用,但对于连续型而言该如何处理?
上文提到,Hinton曾经在他的文章中给出过非二值的受限玻尔兹曼的条件概率公式(假定来自于均值为μ,方差为σ的高斯分布),在给出这个公式推导之前,先重新定义下能量:
上述公式是令显层的神经元是实值,而隐层神经元取值仍在{0,1}两个离散值之间,根据相关对称性,可以想见如果显层和隐层均为实值变量的话,则公式15应为:
对于公式15和公式16应注意其符号的变化。但Hinton又在他的课程中指出,如果存在方差则造成训练的失败,那么我们可以令方差σ=1,那么公式16就变成:
以下我们就在这个基础上推导相关条件概率公式。这里需要强调的是其实推导本身没有什么复杂的,只不过使用了点积分知识,而且需记住在多元函数积分中,如果需要消除哪个变量那么就应该对其进行积分,类似地对于离散情况也是如此,只不过把积分符号改成了求和符号而已;另外,通过下面的证明来看,消除一个变量总比消除多个变量来的方便些,公式看上去也简单明了不少,否则按照贝叶斯公式的标准表达,则我们要进行多重积分以求得相关边缘分布。
由上节的基于二值受限玻尔兹曼机公式14启发得:
至此我们得到了显层对隐层的条件概率,而由其对称性可知隐层对显层的条件概率为:
最终,对于非二值受限玻尔兹曼机的推导完成,请各位指正。至于算法流程和如何利用对比散度来进行抽样,则这部分其实和二值受限玻尔兹曼机无甚区别,只不过对于后者而言是利用平均抽取,而前者采用正态分布抽取而已。
原文地址:http://13345387.blog.51cto.com/13335387/1971665