标签:合数 递推公式 第一个 tip 二维 输入 move 相同 next
课后作业1
一.使用组合数公式利用n!来计算
1.程序设计思想
①提示用户输入n和k的值。
②判断n是否类型正确,若不正确结束程序。
③判断k是否类型正确,若不正确结束程序。
④判断n是否大于等于k,若是,继续运行程序,否则结束程序。
⑤调用计算阶乘的方法,在此方法中,若输入的数字为0或1,返回1;若不是,则用递归的方法重复调用此方法计算阶乘。
2.程序流程图
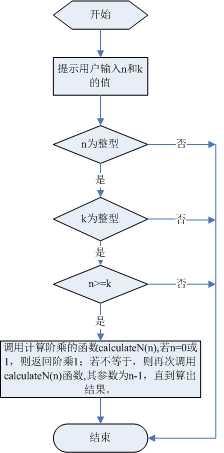
3.程序源代码
import java.util.Scanner; import java.math.BigInteger; public class CombinatorialNumber1 { /** * @param args */ public static void main(String[] args) { // TODO Auto-generated method stub System.out.println("求n!/(k!*(n-k)!),请输入n和k:");//提示用户输入n和k Scanner input=new Scanner(System.in); int n=0,k=0; if(input.hasNextInt())//判断n是否是整型 { n=input.nextInt();//输入n的值 } else//n输入的不是整型,报错并结束程序 { System.out.println("您输入的数据有错!"); System.exit(0); } if(input.hasNextInt())//判断k是否是整型 { k=input.nextInt();//输入k的值 } else//n输入的不是整型,报错并结束程序 { System.out.println("您输入的数据有错!"); System.exit(0); } if(n>=k)//因要求(n-k)!,所以需要判断n>=k是否成立 { //调用方法分别计算n!、k!、(n-k)!,计算最后结果并输出 System.out.print(n+"!/("+k+"!*("+n+"-"+k+")!))="+calculateN(n).divide((calculateN(k).multiply(calculateN(n-k))))); } else//n<k,无法计算,报错并结束程序 { System.out.println("您输入的数据有错!"); System.exit(0); } } public static BigInteger calculateN(int n) //计算n! { if(n==1||n==0)//判断h是否为1或0,若是,则无需进行递归,其阶乘为1 { return BigInteger.valueOf(1); } return BigInteger.valueOf(n).multiply(calculateN(n-1));//递归调用calculateN方法 } }
4.结果截图
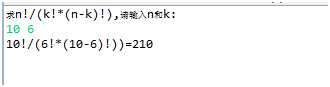
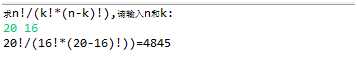
5.实验总结
本题中出现的问题主要是对于BigInteger的使用不熟练,在int型时返回1,而在BigInteger中要用BigInteger.valueOf(1);在BigInteger中的加减乘除需调用对应的函数来实现,而在普通的则用对应的符号就可以。
二. 使用递推的方法用杨辉三角形计算
1.程序设计思想
①提示用户输入组合数的n和k。
②判断n和k是否合法,若不合法,则结束程序;合法,继续程序。
③定义一个(n+1)*(n+1)的二维数组用来放杨辉三角的数值。
④利用循环嵌套完成杨辉三角中每个位置数值的计算。先为每一行赋值,每行的第一个数和最后一个数均为1,其余位置为上一行的第k-1和k个数的和,然后为下一行赋值。
⑤输出指定位置的数值。
2.程序流程图
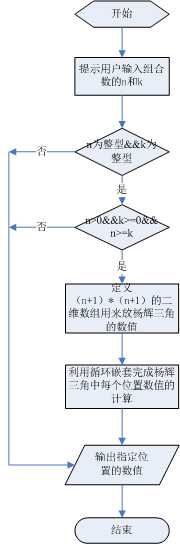
3.程序源代码
import java.util.Scanner; public class YanguiTriangle { /** * @param args */ public static void main(String[] args) { // TODO Auto-generated method stub Scanner input=new Scanner(System.in); int n=0; int k=0; System.out.println("请输入组合数C_n^k的n和k:");//提示用户输入n和k if(input.hasNextInt())//判断类型是否正确 { n=input.nextInt();//类型正确输入n } else//类型不正确报错并结束程序 { System.out.println("输入错误!"); System.exit(0); } if(input.hasNextInt())//判断类型是否正确 { k=input.nextInt();//类型正确输入k } else//类型不正确报错并结束程序 { System.out.println("输入错误!"); System.exit(0); } if(n>0&&k>=0&&n>=k)//判断n和k的值是否合法且n>=k是否成立 { int triangle[][]=new int[n+1][n+1];//定义n+*n+1的数组存放杨辉三角各位置的 for(int i=0;i<=n;i++) { for(int j=0;j<=i;j++) { if(j==0)//每行第一个元素为1 { triangle[i][j]=1; } else if(i==j)//每行最后一个元素为1 { triangle[i][j]=1; } else//为其余位置元素赋值 { triangle[i][j]=triangle[i-1][j-1]+triangle[i-1][j]; } } } System.out.println("结果为:"+triangle[n][k]);//显示用户指定位置的元素的值 } } }
4.结果截图


5.实验总结
本题的问题出现在定义二维数组上,开始想让用户自己输入杨辉三角的高度,后来觉得可能会造成空间的浪费。经过思考,发现可以在用户输入n和k的值后,定义生成n+1*n+1的二维数组,这样造成的浪费会少一点。还有在此程序中需特别注意数组的下标不要弄混。
三.使用递归的方法用组合数递推公式计算
1.程序设计思想
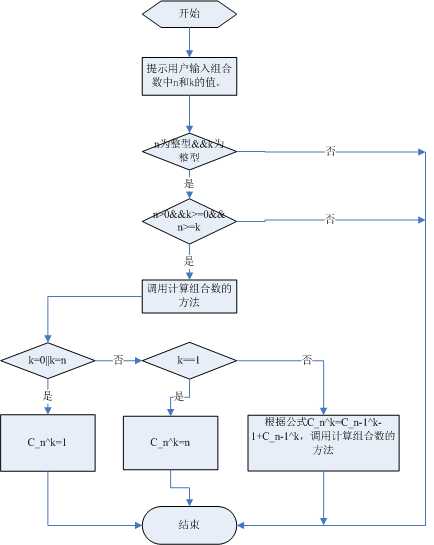
①提示用户输入组合数中n和k的值。
②判断n和k是否合法,若不合法,则结束程序;合法,继续程序。
③定义计算组合数的方法。如果输入的k=0或n,则 =1;如果k=1,则其他情况则根据公式 计算。
④输出结果并结束程序。
2.程序流程图
3.程序源代码
import java.util.Scanner; public class CombinatorialNumber3 { /** * @param args */ public static void main(String[] args) { // TODO Auto-generated method stub System.out.println("请输入组合数C_n^k中的n和k:");//提示用户输入n和k Scanner input=new Scanner(System.in); int n=0,k=0; if(input.hasNextInt())//判断类型是否正确 { n=input.nextInt();//类型正确输入n } else//类型不正确报错并结束程序 { System.out.println("输入错误!"); System.exit(0); } if(input.hasNextInt())//判断类型是否正确 { k=input.nextInt();//类型正确输入k } else//类型不正确报错并结束程序 { System.out.println("输入错误!"); System.exit(0); } if(n>0&&k>=0&&n>=k)//判断n和k的值是否合法且n>=k是否成立 { System.out.println("结果为:"+calculateC(n,k));//成立,输出结果 } else//n<k,无法进行运算,报错并结束程序 { System.out.println("输入错误!"); System.exit(0); } } public static int calculateC(int n,int k)//计算相应的组合数 { if(k==0||k==n)//C_n^0=1或C_n^n=1 { return 1; } else if(k==1)//C_n^1=n { return n; } else//利用公式//C_n^k=C_n-1^k-1+C_n-1^k { return calculateC(n-1,k-1)+calculateC(n-1,k); } } }
4.结果截图


课后作业2
1. 程序设计思想
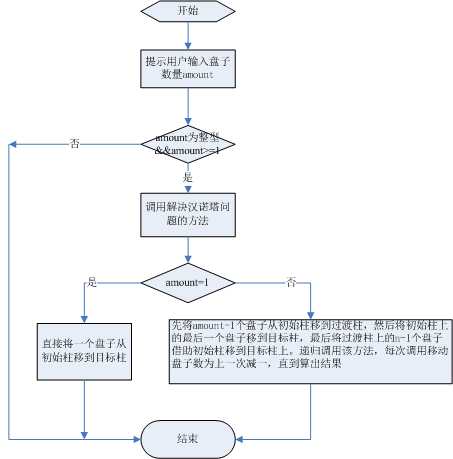
⑴ 提示用户输入盘子数量。
⑵ 调用方法解决汉诺塔问题。
将n个盘子从第一根柱子移到第三根柱子上的方法为:①先将n-1个盘子借助第三根柱子移到第二根柱子上。②再将第一根柱子上的最大的盘子移到第三根柱子上。③然后将第二根柱子上的n-1个盘子借助第一根柱子移到第三根柱子上。
将n-1个盘子从第二根柱子上移到第三根柱子上的方法为:①先将n-2个盘子借助第三根柱子移到第一根柱子上②再将第二根柱子上的最大的盘子移到第三根柱子上。③然后将第一根柱子上的n-2个盘子借助第二根柱子移到第三根柱子上。
而移动n-2个盘子的方法又类似于移动n个盘子的方法,以此类推。上述的第一、二、三根柱子可视为初始柱、过渡柱以及目标柱。移动n个盘子三步可视为:①将n-1个盘子由初始柱借助目标柱移到过渡柱。②将初始柱上的最大的盘子直接移到目标柱。③将n-1个盘子由过渡柱借助初始柱移到目标柱。借助递归的方法可解决汉诺塔的问题。
⑶ 在方法中,先判断盘子数量是否为1,若为1,则直接将第一根柱子上的盘子移到第三根上;否则,先将n-1个盘子移动到过渡柱上,再将初始柱上的盘子移到目标柱上,再将n-1个盘子由过渡柱移到目标柱上。递归调用该方法,每次调用移动的盘子是上一次减一个。
⑷ 直到算出结果,将结果显示在屏幕,程序结束。
2. 程序流程图
3. 程序源代码
import java.util.Scanner; public class Hanoi { /** * @param args */ public static void main(String[] args) { // TODO Auto-generated method stub System.out.println("请输入要放的盘子数量:");//提示用户输入盘子数量 Scanner input=new Scanner(System.in); int amount=0; if(input.hasNextInt()) { amount=input.nextInt();//用户输入数量 } else { System.out.println("输入错误!"); System.exit(0); } if(amount>=1)//判断用户输入的盘子数量是否合法 { hanoi(amount,‘A‘,‘B‘,‘C‘);//调用函数解决汉诺塔问题 } else { System.out.println("输入错误!");//用户输入有误 } } public static void hanoi(int amount,char a,char b,char c)//解决汉诺塔问题 { if(amount==1)//如果盘子数量为1,则直接将其移动到目标柱上 { move(a,c);//移动盘子的函数 } else { hanoi(amount-1,a,c,b);//先将n-1个盘子移到过渡柱上 move(a,c);//将初始柱上的盘子移到目标柱上 hanoi(amount-1,b,a,c);//将n-1个盘子从过渡柱移到初始柱上 } } public static void move(char a,char c)//移动盘子 { System.out.println(a+"--->"+c);//显示从初始柱移到目标柱的过程 } }
4.结果截图


课时作业3
1. 程序设计思想
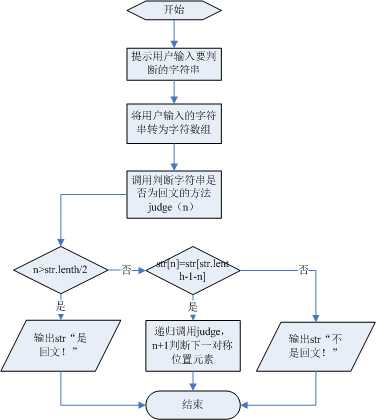
① 提示用户输入字符串。
② 将字符串类型数据转成字符数组便于比较对称位置上的字符。
③ 定义判断是否是回文的方法,参数为每次要判断的字符的位置。若字符的位置超过字符数组的的一半,说明字符串为回文;判断一对对称位置上的字符是否一致,若一致则判断下一对对称位置上的字符是否一致,如不一致则不是回文。
④ 在主函数中调用判断是否一个字符串是否为回文的方法,因为在数组中一个元素下标为0,所以调用时参数应为0,并做相应输出。
2. 程序流程图
3. 程序源代码
import java.util.Scanner; public class Palindrome { /** * @param args */ static char[] str;//定义全局变量字符数组用于放字符串 public static void main(String[] args) { // TODO Auto-generated method stub System.out.println("请输入要判断的字符串:");//提示用户输入字符串 Scanner input=new Scanner(System.in); String string=input.next();//用户输入字符串 str=string.toCharArray();//将字符串转为字符数组便于比较对称的字符是否相同 if(judge(0))//因为在字符数组中第一个字符的下标为0,所以从0开始判断 { System.out.println(string+"是回文!");//显示用户输入的字符串为回文 } else { System.out.println(string+"不是回文!");//显示用户输入的字符串不是回文 } } public static boolean judge (int n)//判断字符串是否是回文 { if(n>=str.length/2)//递归结束的条件:当比较的字符超过字符数组的一半时,说明此时仍没有出现对称位置上的字符不相等的情况,则此字符串为回文 { return true;//返回true } else if(str[n]==str[str.length-1-n])//比较字符数组的对称位置上的字符是否一致 { return judge(n+1);//若对称位置上的字符一致,则判断后一对对称位置上的字符 } else { return false;//递归结束的条件:出现对称位置上的一对字符不一致的情况,则此字符串不是回文,返回false } } }
4. 结果截图


5.实验总结
在本题中用toCharArray函数将字符串转为字符数组便于判断,判断时通过判断每一对称位置上的元素是否一致来判断字符串是不是回文,判断时应从第一个元素位置开始判断,在此处应注意参数为0不是为1,因为在数组中第一个元素下标为0。一致则通过将参数加一来实现位置的移动,当参数位置超过数组长度一半时则为回文,判断有不一致的元素时则不是回文。
标签:合数 递推公式 第一个 tip 二维 输入 move 相同 next
原文地址:http://www.cnblogs.com/qilin20/p/7663628.html