标签:public 公式 bsp main nbsp class 杨辉三角 输入 依次
使用计算机计算组合数:
(1)使用组合数公式利用n!来计算
设计思想:
解决求n的阶乘的函数,利用组合数公式,求组合数,
程序流程图:
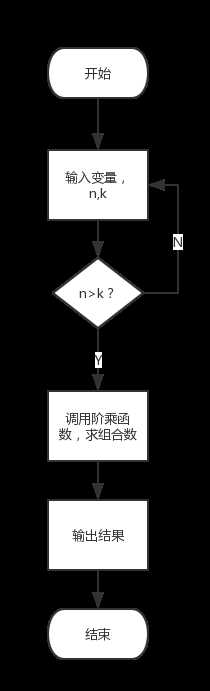
程序源代码:
package text7;
import java.util.Scanner;
public class Num1 {
public static void main(String args[])
{
Scanner input=new Scanner(System.in);
int n,k;
System.out.println("请输入组合数公式的n和k:");
n=input.nextInt();
k=input.nextInt();
while(k>=n)
{
System.out.println("输入错误,请重新输入");
System.out.println("请输入组合数公式的n和k:");
n=input.nextInt();
k=input.nextInt();
}
long C;
C=calculateN(n)/(calculateN(k)*calculateN(n-k));
System.out.println("结果为"+C);
}
public static long calculateN(int n)
{
if(n==1 || n==0){
return 1;
}
return n*calculateN(n-1);
}
}
程序截图:
(2)使用递推的方法用杨辉三角形计算
设计思路:
构建杨辉三角,组合数结果就相当于杨辉三角中的一个数,n为行,k为列,输出相应的数就可以
程序流程图:
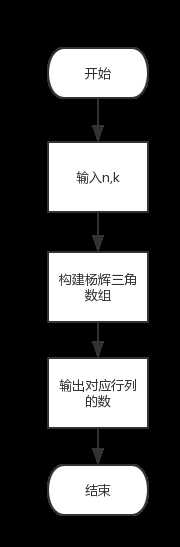
程序代码:
package text8;
import java.util.Scanner;
public class Num2 {
public static void main(String args[])
{
Scanner input=new Scanner(System.in);
int n,k;
System.out.println("请输入组合数公式的n和k:");
n=input.nextInt();
k=input.nextInt();
int [][]f=new int[27][27];
f[0][0] = 1;
for(int i = 1;i <= 24;i++)
{
for(int j = 1;j <= i + 1;j++)
{
f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
}
}
System.out.println("组合结果为"+f[n+1][k+1]);
}
}
程序截图:
(3)使用递归的方法用组合数递推公式计算
设计思路:
递归组合数,和杨辉三角类似, 构建递归函数,n,k相应于杨辉三角的行列
程序流程图:
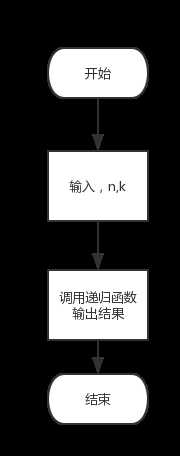
程序代码;
package text9;
import java.util.Scanner;
public class Num3 {
public static void main(String args[])
{
Scanner input=new Scanner(System.in);
int n,k;
System.out.println("请输入组合数公式的n和k:");
n=input.nextInt();
k=input.nextInt();
System.out.println("组合结果为"+ZuHe(n,k));
}
public static long ZuHe(int a,int b)
{
if(b==0)return 1;
else {
if(a==1)return 1;
else {
if(a==b)return 1;
else {
return (ZuHe(a-1,b-1)+ZuHe(a-1,b));
}
}
}
}
}
程序截图:
二 递归编程解决汉诺塔问题。用Java实现
设计思路: 移动n个圆盘,先移动n-1个,再把第n个移动到c上,利用递归,依次移动
程序流程图:
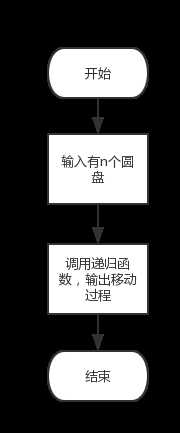
程序源代码;
package text10;
import java.util.Scanner;
public class Han {
public static void main(String args[])
{
int n;//有n个圆盘
char A=‘A‘;
char B=‘B‘;
char C=‘C‘;
Scanner input=new Scanner(System.in);
System.out.println("请输入n:");
n=input.nextInt();
Hanoi( n,A,B,C);
}
public static void Hanoi(int n,char A,char B,char C)
{
if(n==1)
{
move(A,1,C);
}
else
{
Hanoi(n-1,A,C,B);
move(A,n,C);
Hanoi(n-1,B,A,C);
}
}
public static void move(char A,int n,char B)
{
System.out.println("第"+n+"个圆盘从"+A+"->"+B);
}
}
程序截图:

三 使用递归方式判断某个字串是否是回文( palindrome
设计思路:“回文”是指正着读、反着读都一样的句子。比较第一个和最后一个 一次比较如果相同输出。
程序流程图:
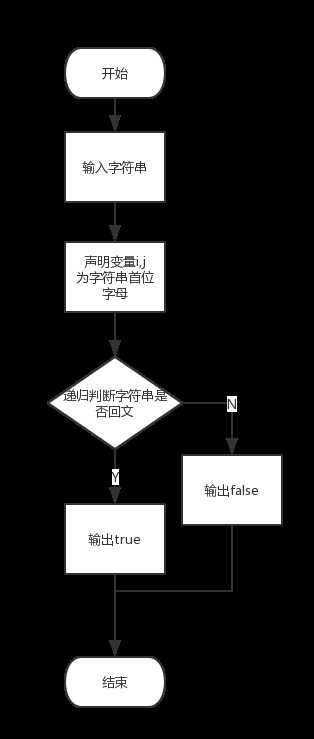
程序代码:
package text11;
import java.util.Scanner;
public class Huiwen {
public static void main(String args[])
{
Scanner input=new Scanner(System.in);
String s=input.next();
int i,j;
i=0;
j=s.length()-1;
System.out.println("是否是回文:"+HuiWen(s,i,j));
}
public static boolean HuiWen(String s,int i,int j)
{
if(i==j)
{
return true;
}
else
if((i-1)==j)
{
return true;
}
return (s.charAt(i)==s.charAt(j))&&HuiWen(s,i+1,j-1);
}
}
程序截图:
标签:public 公式 bsp main nbsp class 杨辉三角 输入 依次
原文地址:http://www.cnblogs.com/gaogege/p/7664230.html