标签:include bool mod 二分 简单 style data can odi
动态规划要学好,姿势一定要骚,在实战的时候,你将你的转移方程按照以下四种姿势搞一发后,一定会是耳目一新,引来萌妹子的注意~~~哈哈!!!
言归正传了!!!
之所以写动态规划优化,是因为常常在动态规划时,你会发现,就算你很轻易地定义出状态,和找到状态转移方程,但是你有可能面临时间限制。动态规划的优化,主要体现在一维上,一维已经很成熟了,也有很多专家研究这个,关于acm的动态规划优化有很多。下面展示几个常用的奇技淫巧。
LIS :?
? : 以 i 号元素为结尾的最长递增子序列长度。
? : 最长递增子序列长度为 i 的最小元素值。
在求 ? 时:只要在 g 数组中二分,同时更新 g 数组。
例题一 :
nyoj 720

分析:类比LIS,同样? 会TLE,将状态定义稍微优化一点, 先按时间排序,? 前 i 个元素能达到的最优值,下一个状态起始时间,就可以在前面的状态中二分到这个时间点。细节有两点,一是,排序因子,因为二分是起始时间,因此得按照右端点优先排序,二是,二分手法,应该是upper_bound。
#include <stdio.h> #include <string.h> #include <math.h> #include <vector> #include <set> #include <map> #include <queue> #include <iostream> #include <algorithm> ? ? using namespace std; ? const int maxn = 5005; ? struct Node { int l,r,v; bool operator < (const Node & rhs) const { if(r==rhs.r) return l < rhs.l; return r < rhs.r; } }nodes[maxn]; ? int n; ? int d[maxn]; ? int upper_bound(int x,int y,int v) { int m; while(x<y) { m = x + (y-x)/2; if(nodes[m].r<=v) x = m+1; else y = m; } return x; } ? int main() { //freopen("in.txt","r",stdin); while(scanf("%d",&n)!=EOF) { for(int i = 0; i < n; i++) { scanf("%d%d%d",&nodes[i].l,&nodes[i].r,&nodes[i].v); } sort(nodes,nodes+n); memset(d,0,sizeof(d)); d[0] = nodes[0].v; for(int i = 1; i < n; i++) { d[i] = max(d[i-1],nodes[i].v); int k = upper_bound(0,i,nodes[i].l); if(k>0&&nodes[k-1].r<=nodes[i].l) d[i] = max(d[i],d[k-1]+nodes[i].v); } printf("%d\n",d[n-1]); ? } return 0; }
还记得括号匹配吗?
Google Code jam 2016 Round3 A;就是一道裸的括号匹配。成功匹配得10分,失败得5分。给定一个序列,求最大得分。因为暂时我电脑连不上Google,原题就不贴了。做法很简单,维护一个栈。
例题二: pku2559

题意:求最大子矩阵面积。
此题是三倍经验题哦,还有一个在51Nod,和一场个人赛GYM上出现过(当时有大佬用KMP搞的);这里利用栈来做到?
分析:无非就是要快速求出一个数字作为最小值(最大值)的左右端点区间。暴力? 实在受不了,这里利用单调栈一下子就降到? 。
维护一个按照高度递增的单调栈,当新加入的矩形破坏了单调栈的单调性,说明一件事情,就是栈顶元素的生命周期已经结束了,他作为最小值的左右端点已经确定。
#include <stdio.h> #include <string.h> #include <math.h> #include <vector> #include <set> #include <queue> #include <stack> #include <iostream> #include <algorithm> ? using namespace std; ? ? const int maxn = 1e5+5; int h[maxn]; ? int main() { //freopen("in.txt","r",stdin); int n; while(scanf("%d",&n),n) { ? for(int i = 1; i <= n; i++) scanf("%d",&h[i]); ? stack<int> S; S.push(0);h[++n] = 0; long long ans = 0; for(int i = 1; i <= n; i++) { while(h[i]<h[S.top()]) { long long a = h[S.top()]; S.pop(); long long b = i - S.top() - 1; if(ans < a*b) ans = a*b; } S.push(i); } ? printf("%lld\n",ans); } return 0; }
例题三:pku 2823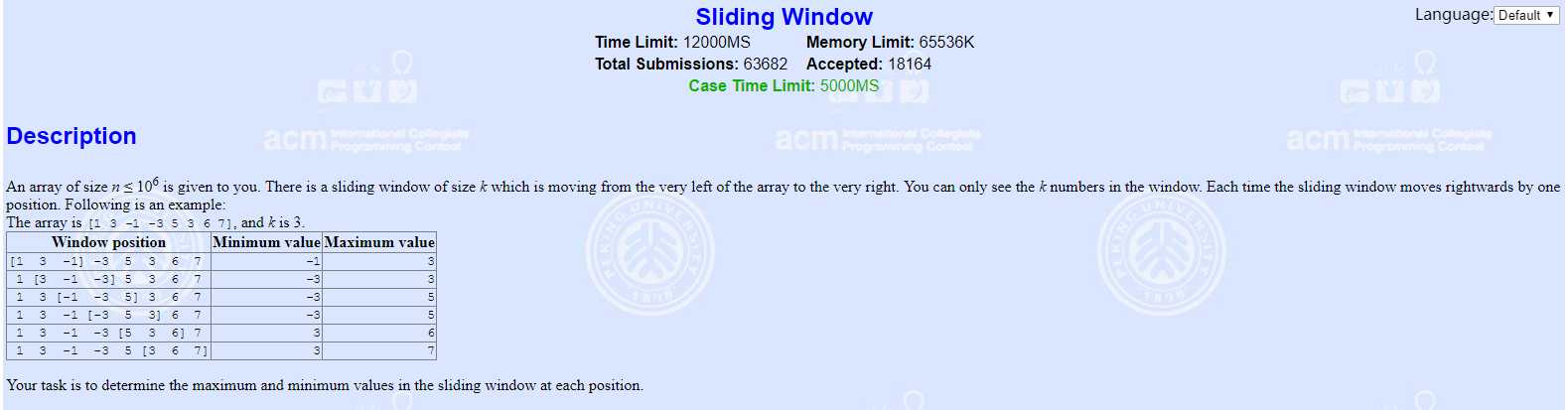

题意:滑动窗口最小值(最大值)
分析:如果你想不到很好的办法,也可以直接上RMQ,?
现在,用? 的解法~~~
维护一个单调自增的队列,同样,如果新加入的数字破坏了队列的单调性,说明队尾的数字将永远不会是这k个数字中的最小值,他已经没用了。
算法具体做法,可能我写的比较渣,大佬很好像合起来写的。
首先,将前k个数字入队列,队首元素就是最小值。
然后加入新的数字,如果破坏了单调性,弹出队尾数字,此时,又一个最小值求出来了,但是这个最小值还要检验一下,是否他还在下一个区间里面。
#include <stdio.h> #include <string.h> #include <math.h> #include <vector> #include <queue> #include <set> #include <map> #include <stack> #include <iostream> #include <algorithm> ? using namespace std; ? const int maxn = 1e6+5; int a[maxn]; ? int main() { //freopen("in.txt","r",stdin); int n,k; cin>>n>>k; ? for(int i = 0; i < n; i++) scanf("%d",&a[i]); deque<int> minq; deque<int> maxq; ? for(int i = 0; i < k; i++) { while(!minq.empty()&&(a[i]<a[minq.back()]) ) { minq.pop_back(); } while(!maxq.empty()&&(a[i]>a[maxq.back()])) { maxq.pop_back(); } minq.push_back(i); maxq.push_back(i); } ? printf("%d ",a[minq.front()]); ? if(minq.front()==0) minq.pop_front(); ? for(int i = k; i < n; i++) { while(!minq.empty()&&(a[i]<a[minq.back()])) { minq.pop_back(); } minq.push_back(i); printf("%d ",a[minq.front()]); if(minq.front()<=i-k+1) minq.pop_front(); } puts(""); ? ? printf("%d ",a[maxq.front()]); ? if(maxq.front()==0) maxq.pop_front(); ? for(int i = k ; i < n; i++) { while(!maxq.empty()&&(a[i]>a[maxq.back()])) { maxq.pop_back(); } maxq.push_back(i); printf("%d ",a[maxq.front()]); if(maxq.front()<=i-k+1) maxq.pop_front(); } puts(""); ? return 0; }
例题四:bzoj 1911

分析:很容易想到类似于LIS的转移。但是数据范围有? ,? 是肯定过不了的。然而,只要稍加转换,
可以发现他是一个斜率公式,然后分析,斜率是凸函数,还是凹函数,只要看符号,这里是大于号,上凸函数中间的点的斜率是不起作用的,那么你应该维护一个斜率单调递增的栈(实际操作中是队列)。
那么最优值在哪里呢?
根据斜率最大,即应该是相切处,那么这时候,你需要根据凹函数的特点了,从前往后遍历,当斜率大于右边,则到达了当前点了。然后加入此节点,也需要维护单调队列的凹函数性质。
关于斜率DP,也是每一个大佬有一种写法,主要不同点在于队列中的点个数上,我习惯于队列中必须有一个结点(有的要两个点),主要是有一个坐标原点。可以实现包含所有可选择区间。具体细节还得自己动手才能发现。
#include <stdio.h> #include <string.h> #include <math.h> #include <vector> #include <queue> #include <string> #include <set> #include <map> #include <iostream> #include <algorithm> ? using namespace std; ? typedef long long ll; const int maxn = 1e6+5; ? long long a,b,c; long long x[maxn]; long long sum[maxn]; long long d[maxn]; double slope(int i,int j) { double up = d[i]-d[j]+a*(sum[i]*sum[i]-sum[j]*sum[j])+b*(sum[j]-sum[i]); double down = 2*a*(sum[i]-sum[j]); return up/down; } int l,r,q[maxn]; int n; ? ? int main() { freopen("in.txt","r",stdin); scanf("%d%lld%lld%lld",&n,&a,&b,&c); ? sum[0] = 0; for(int i = 1; i <= n; i++) { scanf("%lld",&x[i]); sum[i] = sum[i-1] + x[i]; } ? deque<int> deq; ? for(int i = 1; i <= n; i++) { ? double xl = slope(q[l],q[l+1]); while(l<r&&slope(q[l],q[l+1])<sum[i]) { l++; } int now = q[l]; d[i]=d[now]+a*(sum[i]-sum[now])*(sum[i]-sum[now])+b*(sum[i]-sum[now])+c; while(l<r&&slope(q[r-1],q[r])>slope(q[r],i)) r--; q[++r] = i; ? } ? printf("%lld\n",d[n]); ? ? return 0; }
到这里DP优化已经聊的差不多了。其实你会发现我都是1D/1D方程,而实战中也有很多2D/0D方程,比如LCS。
但是他们的优化思路,是还有待大牛研究的课题。
标签:include bool mod 二分 简单 style data can odi
原文地址:http://www.cnblogs.com/TreeDream/p/7668865.html