标签:form 必须 地方 rem 模板 之间 二进制 通过 思路
https://github.com/Slontia/Sudoku2
2. PSP

3. 看教科书和其它资料中关于Information Hiding, Interface Design, Loose Coupling的章节,说明你们在结对编程中是如何利用这些方法对接口进行设计的。
一切的解数独、生成数独的函数都只需要调用 Core 类中的方法,而不必关心 Core 中的具体实现方法和数据存放,有 Information Hiding 的思想
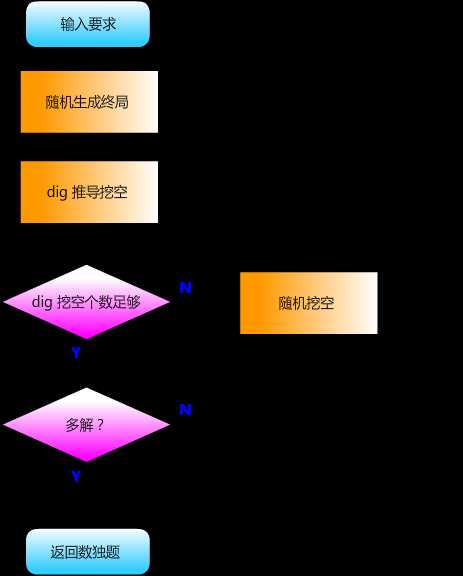
为了快速生成多空单解数独的题目,我们分成了两部,第一步是进行推导式挖空,调用 dig 函数;如果第一步不成功,则第二步进行随机挖掘。
其中 dig 需要比较复杂的数据结构,和随机挖空的情形十分不同,因此设计接口和随机挖掘耦合:
int dig(int mat[SIZE*SIZE], int out[SIZE*SIZE], int dig_count);
dig 的界面很简单:输入数独矩阵 mat 和挖掘目标 dig_count,输出挖空结果到 out,返回实际挖空个数。dig 内部在函数栈里需要生成特殊的数据结构,但对外部都不可见。
同时,这里运用了 Louse Couping 的设计,out 可以视为传递的介质,这里牺牲了效率,将矩阵读入进行处理再读出,而不是和随机挖空使用统一的数据结构,但是这个代价相比尝试挖空的过程,消耗可以不计,而增加了开发的敏捷性。
FgMap 是一个类,用来记录每个单元(宫、列、行)的逻辑属性;UnitMaps 则统合了一共 9 * 3 个 FgMap,UnitMaps 通过调用 FgMap 的方法,对 FgMap 进行遍历访问,将信息填入 FgMap 并且获得 FgMap 的逻辑结论,而不用关心 FgMap 中的信息如何管理和结论如何得出。
dig 将数字信息输入 UnitMaps,从 UnitMaps 中获得当前被其他数字确定的位置,进行挖空,从而使得被挖掉的数字可以被其他数字(用数独的一个定理的子集)推导出来。
4. 计算模块接口的设计与实现过程。设计包括代码如何组织,比如会有几个类,几个函数,他们之间关系如何,关键函数是否需要画出流程图?说明你的算法的关键(不必列出源代码),以及独到之处。
主要有三个模块:
1. create 模块
这次作业虽然指定不允许出现等价数独,但我们还是可以通过模板变换快速生成1000000个数独。首先,我们需要保证数独的等价性,我们的做法是不对第一个宫进行任何操作(随机性貌似在-c不做要求?)。我们沿用了刘畅同学在个人项目中使用的3-3-3位置轮换方法成功生成了一个数独终盘。在个人项目中,模板的变化主要体现在R4~R6、R7~R9的行变换,但其实,对于3-3-3位置轮换方法生成的终盘,部分行的变换也是可行的,如下图:
//图片暂无
由此可以看出,改变部分行可以产生12种排列,而不同颜色之间的变化由相互独立,R4~R6和R7~R9相互独立,共有6组相互独立的变换,共可以产生12的6次方共2985984种排列。
2. solve 模块
solve模块的实现和个人项目相同。
3. puzzle 模块
独到之处:
1. 选择最有效的随机方式。我们在随机挖空的时候,发现纯粹随机的效果并不好,特别是要求生成55个空的独解数独时,会比较慢。但是如果在各个宫内部进行比较平均的挖空,得出来的空会分布得比较均匀,就容易产生单解数独。
2. 结合逻辑推导。反向使用行列宫摈除法,可以挖掉当前局面来看具有逻辑必然性的数字(比如说第一行是 1 2 3 4 5 6 7 8 9,那么 1 可以被挖掉,因为 1 的存在是被其他 8 个数决定的),这样,这部分的挖空可以不用交给随机挖空来解决,降低了算法的时间复杂度。
5. UML
 6)计算模块接口部分的性能改进。记录在改进计算模块性能上所花费的时间,描述你改进的思路,并展示一张性能分析图(由VS 2015/2017的性能分析工具自动生成),并展示你程序中消耗最大的函数。
6)计算模块接口部分的性能改进。记录在改进计算模块性能上所花费的时间,描述你改进的思路,并展示一张性能分析图(由VS 2015/2017的性能分析工具自动生成),并展示你程序中消耗最大的函数。
1. puzzle 模块
1. 测试指令 -n 10000 -r 20~35 -u
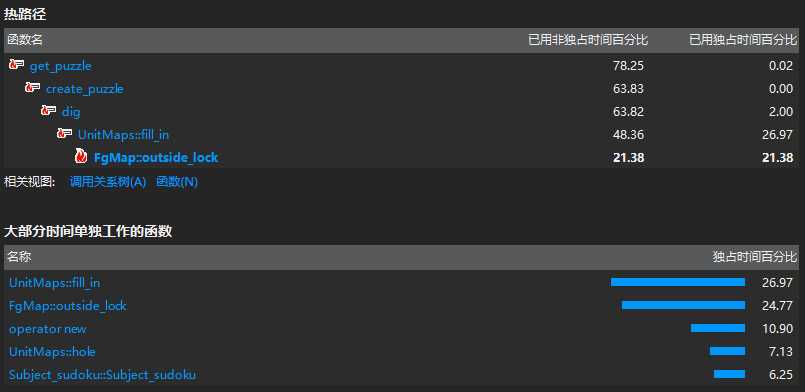
2. 测试指令 -n 10000 -r 36~50 -u
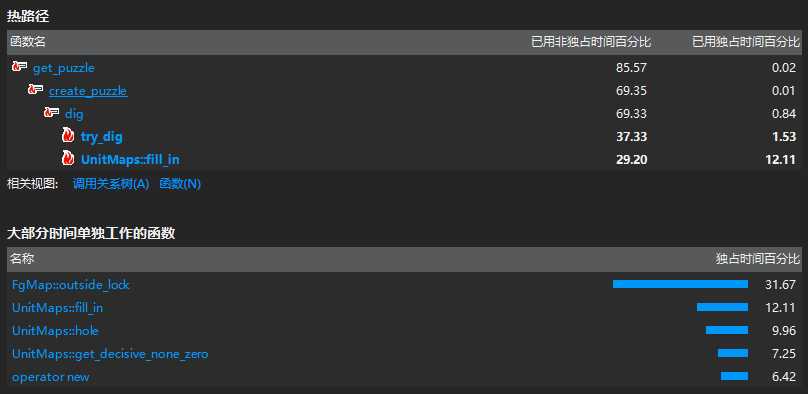
3. 测试指令 -n 10000 -r 51~55 -u
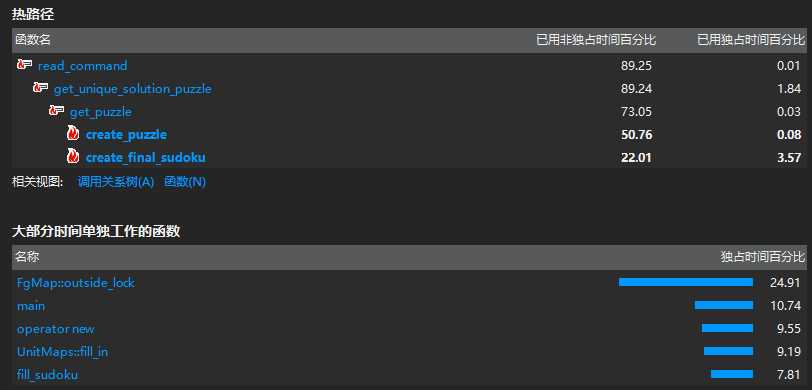
`可见,FgMap::outside_lock 是最耗时间的函数,编写之前已经考虑到了这个问题,因此采用了位运算等加速方法,实际上很难再优化了。
2. create 模块
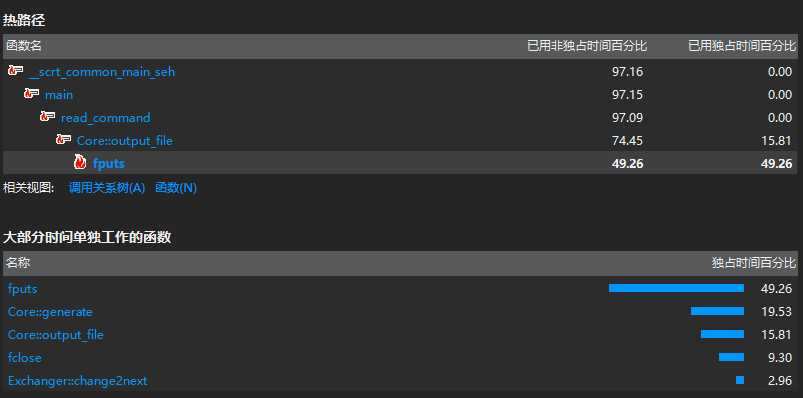
create 采用的是行列交换的方法生成不等价的数独,因此很快,瓶颈在 io,但这里采用了缓存一次性输出的方式,最大限度利用了 block 读写的功能,因此也无法再优化了。
3. solve 模块
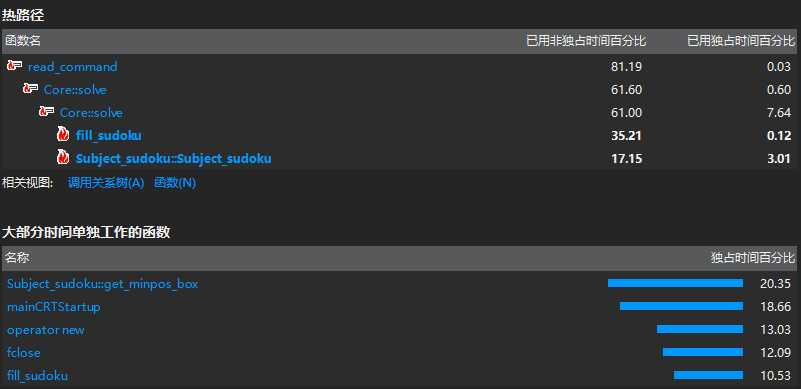
7)描述这些做法的优缺点, 说明你是如何把它们融入结对作业中的。
契约式编程:
前置条件(pre-condition)、后置条件(post-condition)和不变式(invariant), 分别指代函数核心逻辑 运行前必须满足的条件、运行后必须满足的条件和运行结果必须保持的不变式(某一不变条件)。
整个sudoku可以认为遵循这样的契约:
1. 前置条件:命令行参数符合语法,数值范围在作业要求范围内(否则 read_command 在读入命令时报错)
2. 后置条件:输出符合要求的数独的解或数独题
3. 不变式:输出符合要求的数独的解或数独题
至于内部各个模块的交互,也在一定程度上应用了契约式编程的思想用于调试,例如:
if ((~map[F2INDEX(figure_x)]) & INDEX2TARGETBIT(index)) { // 假如原来这个可能性已经被删除了,意味着取反以后这个位置为 1 limit[F2INDEX(figure_x)][index] --; assert(limit[F2INDEX(figure_x)][index] >= 0); if (limit[F2INDEX(figure_x)][index] == 0) { pos_count[F2INDEX(figure_x)]++; map[F2INDEX(figure_x)] |= INDEX2TARGETBIT(index); } ret = true; }
这里对 limit 进行判断,要是它小于 0,就直接 crash。这要求其他部分对 limit 处理是恰当的,否则这块代码将无法正确执行。
bool UnitMaps::fill_in(int figure, int i, int j) { int group_id = GET_GROUP_ID(i, j); blank--; assert(figure != 0); assert(matrix[i][j] == 0); // ...... }
这里要求一定在数独矩阵填 0 的地方才能填数,而且填的数不能是 0 。假如其他部分指定figure , i , j 不正确,就可以及时报错。
优点:
如果把模块尽量做得小而可以维护,那么契约式编程可以极大提高程序的正确性,而且可以极大降低调试的代价。
缺点:
1. 全面考虑三个条件比较复杂,特别是系统还没有实现的时候,事实上输入输出比较复杂的时候,也很难全面考虑清楚。
2. 无论输入是否可以信任,程序运行时总在判断合法性,效率比较低。
3. 软件总是容易有 bug ,契约式编程实际上很难维持契约的严格正确性。
8)计算模块部分单元测试展示。展示出项目部分单元测试代码,并说明测试的函数,构造测试数据的思路。并将单元测试得到的测试覆盖率截图,发表在博客中。要求总体覆盖率到90%以上,否则单元测试部分视作无效。
我们沿用了个人项目中的字典树重复性判断,这次新添了检测等价性的功能。我们选取第一个宫,对里面的数字分别和1~9进行映射,之后将整个数独根据映射刷新,再放入字典树中进行判断。映射的代码如下:

1 char digit_map[SIZE]; 2 for (int i = 0; i < SIZE; i++) { 3 digit_map[i] = (*sudoku)[i]; // build map 4 } 5 /* change to equivalence */ 6 for (int i = 0; i < SIZE * SIZE; i++) { 7 (*sudoku)[i] = digit_map[(*sudoku)[i] - ‘1‘]; 8 }
9)计算模块部分异常处理说明。在博客中详细介绍每种异常的设计目标。每种异常都要选择一个单元测试样例发布在博客中,并指明错误对应的场景。
InvalidCommandException 错误的指令;

1 TEST_METHOD(command_exception1) { 2 bool test_result = false; 3 int argc = 4; 4 char* argv[10] = { 5 "sudoku.exe", 6 "-s", 7 "100", 8 "-c" 9 }; 10 try { 11 read_command(argc, argv); 12 } 13 catch (InvalidCommandException*) { 14 test_result = true; 15 } 16 Assert::IsTrue(test_result); 17 }
CannotOpenFileException 无法打开文件;

1 TEST_METHOD(cannot_open) { 2 bool test_result = false; 3 Core core; 4 try { 5 core.input_file("puz.txt", result_solve); 6 } 7 catch (CannotOpenFileException* e) { 8 test_result = true; 9 } 10 Assert::IsTrue(test_result); 11 }
BadFileException 文件异常或损坏;

1 TEST_METHOD(incompleted_sudoku) { 2 FILE* ftest; 3 int erno = fopen_s(&ftest, "puzzle.txt", "w"); 4 if (ftest == NULL) { 5 cout << erno << endl; 6 Assert::Fail(); 7 } 8 Core core; 9 fputs( 10 "4 1 7 2 3 8 6 5 9\n\ 11 3 2 6 4 9 5 8 1 7\n12 9 5 8 7 1 6 3 2 4\n13 6 9 1 8 5 2 7 4 3\n14 8 4 2 9 7 3 1 6 5\n15 7 3 5 6 4 1 9 8 2\n16 1 8 3 5 2 7 4 9 6\n17 2 7 9 1 6 4 5 3 8\n18 5 6 4 3 8 9 2 7 b" 19 , ftest); 20 fclose(ftest); 21 bool test_result = false; 22 try { 23 core.input_file("puzzle.txt", result_solve); 24 } 25 catch (BadFileException* e) { 26 test_result = true; 27 } 28 Assert::IsTrue(test_result); 29 }
InvalidPuzzleException 数独谜题本身不符合规则(并非指全部无解谜题)。

1 TEST_METHOD(invalid_puzzle) { 2 bool test_result = false; 3 int puzzle[SIZE*SIZE] = 4 { 5 1, 1, 0, 0, 0, 0, 0, 0, 0, 6 0, 0, 0, 0, 0, 0, 0, 0, 0, 7 0, 0, 0, 0, 0, 0, 0, 0, 0, 8 0, 0, 0, 0, 0, 0, 0, 0, 0, 9 0, 0, 0, 0, 0, 0, 0, 0, 0, 10 0, 0, 0, 0, 0, 0, 0, 0, 0, 11 0, 0, 0, 0, 0, 0, 0, 0, 0, 12 0, 0, 0, 0, 0, 0, 0, 0, 0, 13 0, 0, 0, 0, 0, 0, 0, 0, 0 14 }; 15 try { 16 test_s(puzzle, false); 17 } 18 catch (InvalidPuzzleException* e) { 19 test_result = true; 20 } 21 Assert::IsTrue(test_result); 22 }
以上样例全部测试通过。
10)界面模块的详细设计过程。
我们主要的GUI界面只有一个,其它的还包括排行榜界面和成绩写入界面。
GUI的布局使用代码生成,没有使用.ui文件,原因是觉得.ui文件自动生成的代码很臃肿,而自己写的话可以建立数组管理各个组件(大概是我们没有找到正确的方法?)。绘图部分就不细说了,主要将一些逻辑处理部分。
首先是新游戏的开始,这里根据Core的generate接口处理数独界面,将未被挖空的数独对应按钮置为Disable:

1 int index = 0; 2 int digit; 3 QPushButton* btn; 4 for (int i = 0; i < SIZE; i++) { 5 for (int j = 0; j < SIZE; j++) { 6 int digit = puzzle[index++]; 7 btn = buttons[i][j]; 8 if (digit == 0) { // free grid 9 btn->setText(""); 10 btn->setEnabled(true); 11 btn->setStyleSheet(UNCERTAIN_GRID_STYLE); 12 numbers[i][j] = 0; 13 } 14 else { 15 char num[2] = { ‘0‘ + digit, ‘\0‘ }; 16 btn->setText(num); 17 btn->setEnabled(false); 18 btn->setStyleSheet(CERTAIN_GRID_STYLE); 19 numbers[i][j] = digit; 20 } 21 } 22 }
这次我们实现的功能有四个,除了要求的check和tip外,我们还附加了filter和track功能。filter是在当前格子内切换所有满足填入规则的值,而track是将某种数字标红便于查看。
check的设计思路是建立三个数组,分别对应行、列、组,并将每一个格子的数字分别存储于这三个数组中,假如某个数组储存的某种数字的数量大于1,说明出现了数字的重复,将重复的数字标红:

1 int row_digit_counter[SIZE][SIZE] = { 0 }; 2 int column_digit_counter[SIZE][SIZE] = { 0 }; 3 int block_digit_counter[SIZE][SIZE] = { 0 }; 4 5 bool pass = true; 6 7 // store box 8 for (int i = 0; i < SIZE; i++) { 9 for (int j = 0; j < SIZE; j++) { 10 int value = numbers[i][j]; 11 if (value != 0) { 12 row_digit_counter[i][value - 1]++; 13 column_digit_counter[j][value - 1]++; 14 block_digit_counter[GET_BLOCKNO(i, j)][value - 1]++; 15 } 16 else { 17 pass = false; 18 } 19 } 20 } 21 22 // judge & initial 23 for (int i = 0; i < SIZE; i++) { 24 for (int j = 0; j < SIZE; j++) { 25 int value = numbers[i][j]; 26 if (value != 0 && ( 27 row_digit_counter[i][value - 1] > 1 || 28 column_digit_counter[j][value - 1] > 1 || 29 block_digit_counter[GET_BLOCKNO(i, j)][value - 1] > 1 30 )) { 31 buttons[i][j]->setStyleSheet(WRONG_GRID_STYLE); 32 pass = false; 33 } 34 else { 35 RESTORE_GRID_STYLE(buttons[i][j]); 36 } 37 } 38 }
tip的实现非常简单,就是将终局数独对应的数字填入就好,这里就不细说了。tracker的实现也很简单,就是找到对应的数字并涂红就好,这里简要说一下filter的实现:
我采用了二进制存储的方法,将当前选中格子所在行、列、宫中出现的所有数字进行记录,得到所有可取的值。但是由于filter所填入的数字是需要不断轮换的,所以我要从当前填入的数字开始进行for循环,保证下一个出现的数字是在当前填入数字之后的。但是假如没有可以填入的数字,我们就将这个格子清空(填入CLEAN)。

1 if (curbtn != NULL) { 2 GO_THROUGH_BLOCKS(GET_BLOCKNO(this->cur_rowno, this->cur_colno)) { 3 int digit = numbers[i][j]; 4 if (digit != 0 && (i != this->cur_rowno || j != this->cur_colno)){ 5 binary_recorder |= (bit << (digit - 1)); 6 } 7 } 8 for (int i = 0; i < SIZE; i++) { 9 int digit; 10 digit = numbers[i][this->cur_colno]; 11 if (digit != 0 && i != this->cur_rowno) { 12 binary_recorder |= (bit << (digit - 1)); 13 } 14 digit = numbers[this->cur_rowno][i]; 15 if (digit != 0 && i != this->cur_colno) { 16 binary_recorder |= (bit << (digit - 1)); 17 } 18 } 19 int cur_digit = numbers[this->cur_rowno][this->cur_colno]; 20 for (int digit = cur_digit + 1; digit <= SIZE; digit++) { 21 if ((binary_recorder & (bit << (digit - 1))) == 0) { 22 set_number(digit); 23 return; 24 } 25 } 26 for (int digit = 1; digit <= cur_digit; digit++) { 27 if ((binary_recorder & (bit << (digit - 1))) == 0) { 28 set_number(digit); 29 return; 30 } 31 } 32 set_number(CLEAN);
11)界面模块与计算模块的对接。详细地描述UI模块的设计与两个模块的对接,并在博客中截图实现的功能。(4‘)
对接很简单,利用core的生成难度谜题功能和求解功能(用于提示功能),将谜题和解储存在数独中。
FILE* fout; this->mode = difficulty - 1; this->unfilled_grid_count = 0; int puzzle_receiver[1][SIZE*SIZE]; core->generate(1, difficulty, puzzle_receiver); for (int i = 0; i < SIZE; i++) { for (int j = 0; j < SIZE; j++) { int gridno = GET_GRIDNO(i, j); this->puzzle[gridno] = puzzle_receiver[0][gridno]; if (puzzle[gridno] == 0) { unfilled_grid_count++; } } } char unfilled_grid_count_str[3]; sprintf(unfilled_grid_count_str, "%d", unfilled_grid_count); grid_count->setText(REMAINING_TEXT + unfilled_grid_count_str); core->solve(puzzle_receiver[0], this->sudoku);
标签:form 必须 地方 rem 模板 之间 二进制 通过 思路
原文地址:http://www.cnblogs.com/wangchenyu1996/p/7669125.html