题目描述
2020年,人类在火星上建立了一个庞大的基地群,总共有n个基地。起初为了节约材料,人类只修建了n-1条道路来连接这些基地,并且每两个基地都能够通过道路到达,所以所有的基地形成了一个巨大的树状结构。如果基地A到基地B至少要经过d条道路的话,我们称基地A到基地B的距离为d。
由于火星上非常干燥,经常引发火灾,人类决定在火星上修建若干个消防局。消防局只能修建在基地里,每个消防局有能力扑灭与它距离不超过2的基地的火灾。
你的任务是计算至少要修建多少个消防局才能够确保火星上所有的基地在发生火灾时,消防队有能力及时扑灭火灾。
输入输出格式
输入格式:
输入文件名为input.txt。
输入文件的第一行为n (n<=1000),表示火星上基地的数目。接下来的n-1行每行有一个正整数,其中文件第i行的正整数为a[i],表示从编号为i的基地到编号为a[i]的基地之间有一条道路,为了更加简洁的描述树状结构的基地群,有a[i]<i。
输出格式:
输出文件名为output.txt
输出文件仅有一个正整数,表示至少要设立多少个消防局才有能力及时扑灭任何基地发生的火灾。
输入输出样例
输入样例#1:
6 1 2 3 4 5
输出样例#1:
 100分 贪心
100分 贪心
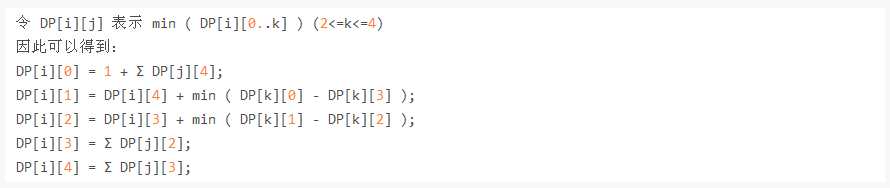
 100分 树形dp
100分 树形dp
2

/* 贪心 按点的深度排序,每次拿出未被更新的最深的点把他的k级父亲标记 可以算是一种模板思路了,在本题中k=2 */ #include<iostream> #include<cstdio> #include<cstring> #define maxn 100010 using namespace std; int cut,ans,m,n,K,t,num,head[maxn],fa[maxn],f[maxn],q[maxn]; int Head,Tail; struct ndoe{ int from,to,pre; }e[maxn*2]; void Insert(int from,int to){ e[++num].from=from; e[num].to=to; e[num].pre=head[from]; head[from]=num; } void bfs(){ Head=Tail=1; q[Tail++]=1; fa[1]=1; while(Head<Tail){ int now=q[Head++]; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(!fa[to]){ fa[to]=now;q[Tail++]=to; } } } } void update(int now){ if(!f[now])return; for(int i=head[now];i;i=e[i].pre){ int to=e[i].to; if(f[to]<f[now]-1) f[to]=f[now]-1,update(to); } } int main(){ int x,y; K=2; scanf("%d",&n); for(int i=1;i<n;i++){ scanf("%d",&y); Insert(i+1,y);Insert(y,i+1); } bfs(); memset(f,-1,sizeof(f)); for(int i=n;i;i--){ if(f[q[i]]==-1){ int j=q[i]; for(int k=K;k;k--)j=fa[j]; ans++;f[j]=K; update(j); } } printf("%d",ans); }

#include<bits/stdc++.h> using namespace std; const int max_n = 1010; const int inf = 1e9+7; int point[max_n],nxt[max_n<<1],v[max_n<<1]; int f[max_n][5]; int n,m,x,tot; inline void init() { memset(point,-1,sizeof(point)); memset(nxt,-1,sizeof(nxt)); tot=-1; } inline void addedge(int x,int y) { ++tot; nxt[tot]=point[x]; point[x]=tot; v[tot]=y; ++tot; nxt[tot]=point[y]; point[y]=tot; v[tot]=x; } void dp(int now,int fa) { int ans1=inf,ans2=inf; if(nxt[point[now]]==-1 && now!=1)//判断是否递归到了叶子节点 { f[now][2]=f[now][0]=f[now][1]=1; f[now][3]=f[now][4]=0; return; } for(int i=point[now]; i!=-1; i=nxt[i]) if(v[i]!=fa) dp(v[i],now); for(int i=point[now]; i!=-1; i=nxt[i]) { if(v[i]==fa) continue; f[now][2]+=f[v[i]][4]; f[now][3]+=f[v[i]][0]; f[now][4]+=f[v[i]][3]; ans1=min(ans1,f[v[i]][2]-f[v[i]][3]); ans2=min(ans2,f[v[i]][1]-f[v[i]][0]); } f[now][0]=f[now][3]+ans2; f[now][1]=f[now][4]+ans1; f[now][2]+=1; f[now][4]=min(min(f[now][0],min(f[now][4],f[now][3])),min(f[now][2],f[now][1])); f[now][3]=min(min(f[now][3],f[now][2]),min(f[now][1],f[now][0])); f[now][0]=min(f[now][0],min(f[now][1],f[now][2])); f[now][1]=min(f[now][1],f[now][2]); } int main() { scanf("%d",&n); init(); for(int i=1; i<n; ++i) { scanf("%d",&x); addedge(i+1,x); } dp(1,0); printf("%d\n",f[1][0]); return 0; }