标签:down setup long bridge length nta gui mini ret
After Karen have found the deterministic winning (losing?) strategy for rock-paper-scissors, her brother, Koyomi, comes up with a new game as a substitute. The game works as follows.
A positive integer n is decided first. Both Koyomi and Karen independently choose n distinct positive integers, denoted by x1,?x2,?...,?xn and y1,?y2,?...,?yn respectively. They reveal their sequences, and repeat until all of 2n integers become distinct, which is the only final state to be kept and considered.
Then they count the number of ordered pairs (i,?j) (1?≤?i,?j?≤?n) such that the value xi xor yj equals to one of the 2n integers. Here xor means the bitwise exclusive or operation on two integers, and is denoted by operators ^ and/or xor in most programming languages.
Karen claims a win if the number of such pairs is even, and Koyomi does otherwise. And you‘re here to help determine the winner of their latest game.
The first line of input contains a positive integer n (1?≤?n?≤?2?000) — the length of both sequences.
The second line contains n space-separated integers x1,?x2,?...,?xn (1?≤?xi?≤?2·106) — the integers finally chosen by Koyomi.
The third line contains n space-separated integers y1,?y2,?...,?yn (1?≤?yi?≤?2·106) — the integers finally chosen by Karen.
Input guarantees that the given 2n integers are pairwise distinct, that is, no pair (i,?j) (1?≤?i,?j?≤?n) exists such that one of the following holds: xi?=?yj; i?≠?j and xi?=?xj; i?≠?j and yi?=?yj.
Output one line — the name of the winner, that is, "Koyomi" or "Karen" (without quotes). Please be aware of the capitalization.
3
1 2 3
4 5 6
Karen
5
2 4 6 8 10
9 7 5 3 1
Karen
In the first example, there are 6 pairs satisfying the constraint: (1,?1), (1,?2), (2,?1), (2,?3), (3,?2) and (3,?3). Thus, Karen wins since 6 is an even number.
In the second example, there are 16 such pairs, and Karen wins again.
判断下xi^yi是否在2n之内。
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 2010; 4 int x[N], y[N]; 5 map<int, int> mp; 6 int main() { 7 int n, ans = 0; 8 cin >> n; 9 for(int i = 1; i <= n; i ++) scanf("%d", &x[i]),mp[x[i]]++; 10 for(int i = 1; i <= n; i ++) scanf("%d", &y[i]),mp[y[i]]++; 11 for(int i = 1; i <= n; i ++) { 12 for(int j = 1; j <= n; j ++) { 13 if(mp.count(x[i]^y[j])) ans++; 14 } 15 } 16 if(ans%2) printf("Koyomi\n"); 17 else printf("Karen\n"); 18 return 0; 19 }
Even if the world is full of counterfeits, I still regard it as wonderful.
Pile up herbs and incense, and arise again from the flames and ashes of its predecessor — as is known to many, the phoenix does it like this.
The phoenix has a rather long lifespan, and reincarnates itself once every a! years. Here a! denotes the factorial of integer a, that is, a!?=?1?×?2?×?...?×?a. Specifically, 0!?=?1.
Koyomi doesn‘t care much about this, but before he gets into another mess with oddities, he is interested in the number of times the phoenix will reincarnate in a timespan of b! years, that is, 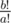 . Note that when b?≥?a this value is always integer.
. Note that when b?≥?a this value is always integer.
As the answer can be quite large, it would be enough for Koyomi just to know the last digit of the answer in decimal representation. And you‘re here to provide Koyomi with this knowledge.
The first and only line of input contains two space-separated integers a and b (0?≤?a?≤?b?≤?1018).
Output one line containing a single decimal digit — the last digit of the value that interests Koyomi.
2 4
2
0 10
0
107 109
2
In the first example, the last digit of 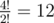 is 2;
is 2;
In the second example, the last digit of 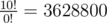 is 0;
is 0;
In the third example, the last digit of 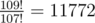 is 2.
is 2.
就是a*(a+1)*...*b; 然后判断下0 1 2..9的数量就行。
1 #include <bits/stdc++.h> 2 #define ll long long 3 ll a[12]; 4 using namespace std; 5 6 int main() { 7 ll a, b, ans = 1; 8 cin >> a >> b; 9 ll num = b - a; 10 if(num >= 10) printf("0\n"); 11 else { 12 for(ll i = a+1; i <= b; i ++) { 13 ans = ans*i%10; 14 } 15 printf("%lld\n", ans); 16 } 17 return 0; 18 }
— This is not playing but duty as allies of justice, Nii-chan!
— Not allies but justice itself, Onii-chan!
With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they‘ve never reached — water-surrounded islands!
There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of a, b and c distinct islands respectively.
Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length 1. For any two islands of the same colour, either they shouldn‘t be reached from each other through bridges, or the shortest distance between them is at least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.
The Fire Sisters are ready for the unknown, but they‘d also like to test your courage. And you‘re here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo 998?244?353. Two ways are considered different if a pair of islands exist, such that there‘s a bridge between them in one of them, but not in the other.
The first and only line of input contains three space-separated integers a, b and c (1?≤?a,?b,?c?≤?5?000) — the number of islands in the red, blue and purple clusters, respectively.
Output one line containing an integer — the number of different ways to build bridges, modulo 998?244?353.
1 1 1
8
1 2 2
63
1 3 5
3264
6 2 9
813023575
In the first example, there are 3 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is 23?=?8.
In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.
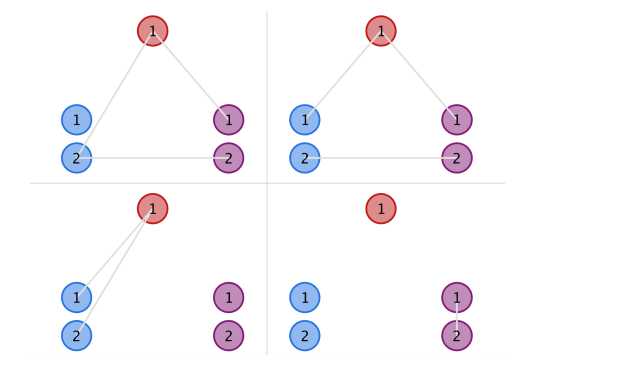
题意好难懂,给3个集合,求同色的最短路大于等于3或者不连通,公有多少种连法。
求出a-b b-c c-a然后相乘。
1 #include <bits/stdc++.h> 2 #define ll long long 3 const ll mod = 998244353; 4 using namespace std; 5 const int N = 5010; 6 ll f[N][N]; 7 int main() { 8 ll a, b, c; 9 cin >> a >> b >> c; 10 for(ll i = 1; i <= 5000; i ++) f[i][1] = f[1][i] = i+1; 11 for(ll i = 2; i <= 5000; i ++) { 12 for(ll j = 2; j <= 5000; j ++) { 13 f[i][j] = f[i-1][j] + f[i-1][j-1]*j%mod; 14 f[i][j] %= mod; 15 } 16 } 17 ll ans = (f[a][b]*f[b][c]%mod)*f[c][a]%mod; 18 printf("%lld\n",ans); 19 return 0; 20 }
Codeforces Round #439 (Div. 2)(ABC)
标签:down setup long bridge length nta gui mini ret
原文地址:http://www.cnblogs.com/xingkongyihao/p/7672948.html