(一)单变量线性回归。
举个例子来说,假如你要在北京的五环路租房,要预测房子的价格,其中一个比较显著的
特征就是房子的面积,根据不同的房间的面积来预测租金是多少。于是你就可以构建一个模型
横轴是房间面积,纵轴是租金。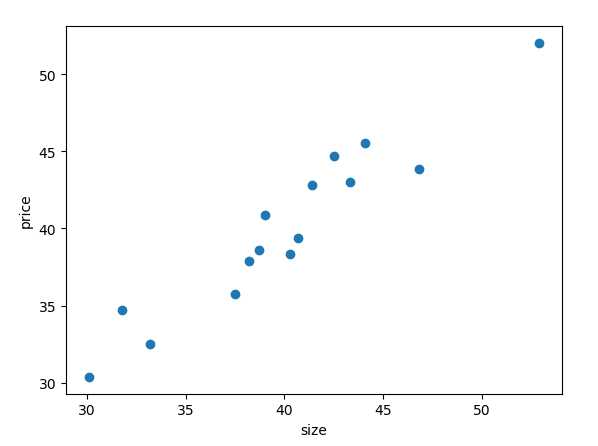
横轴是房间面积,纵轴是租金。从图中我们可以看出这些点所在的位置近乎是在一条直线上面的。
这就是一个回归问题,回归一词指的是,我们根据之前的数据即房子面积预测出一个准确的输出值(租金)。
所以,我们写一个假设函数。通常表示为小写 h。h 代表 hypothesis(假设) ,h 表示一个函数,输入是房间的面积,
因此h根据输入的x值来得出y值,y值对应房子的租金。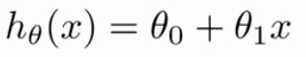
我们现在要做的便是为我们的模型选择合适的参数theta0和theta1,在租金问题这个例子中便是直线的斜率和在
y 轴上的截距。 我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的值与训练
集中实际值之间的差距(下图中蓝线所指)就是建模误差。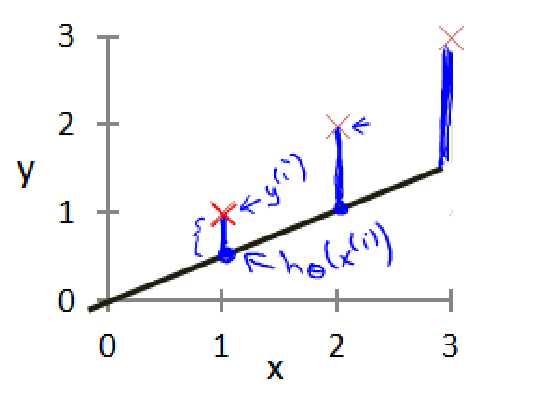
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。建模误差的平方和便是代价函数(cost function),又叫误差平方代价函数。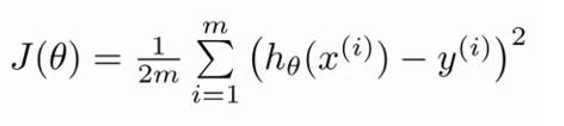
目标就是要让代价函数最小。
来看一下代价函数在等高线图中的样子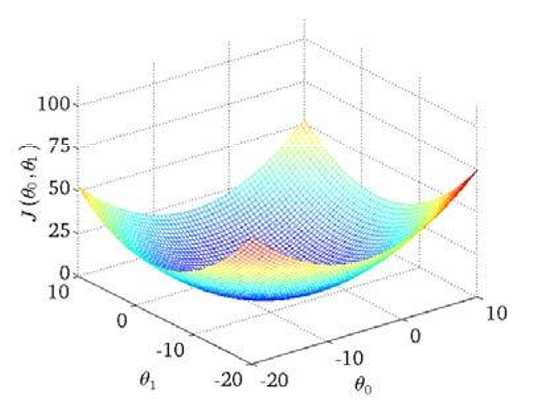
从图中可以看出在三维空间中存在一个最低点。也就是使得代价函数最小的点。
那么如何找到代价函数的最小值呢,现在引入一个比较常用的算法,梯度下降算法。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合,计算代价
函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到到
一个局部最小值,因为我们并没有尝试完所有的参数组合,所以不能确定
我们得到的局部最小值是否便是全局最小值,选择不同的初始参数组合,
可能会找到不同的局部最小值。 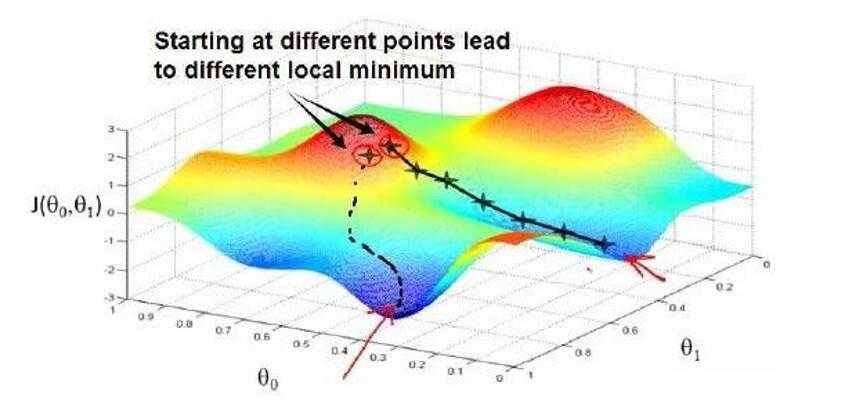
想象一下你正站立在山的这一点上,站立在你想象的公园这座红色山上,在梯度下降算法中,我们要做的就是旋转 360 度,看看我们的周围,并问自己要在某个方向上,用小碎步尽快下山。这些小碎步需要朝什么方向?如果我们站在山坡上的这一点,你看一下周围,你会发现最佳的下山方向,你再看看周围,然后再一次想想,我应该从什么方向迈着小碎步下山?然后你按照自己的判断又迈出一步,重复上面的步骤,从这个新的点,你环顾四周,并决定从什么方向将会最快下山,然后又迈进了一小步,并依此类推,直到你接近局部最低点的位置。 这个步子的大小就是学习速率α。梯度下降算法的每次迭代受到学习率的影响,如果学习率 α 过小,则达到收敛所需的迭代次数会非常高;如果学习率 α 过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率: α=0.01,0.03,0.1,0.3,1,3,10
对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即: 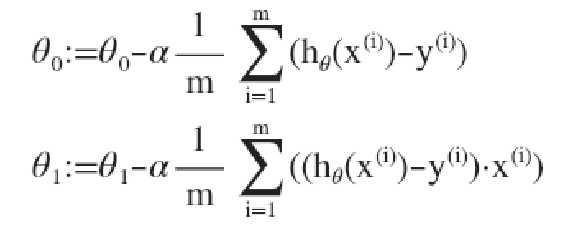
推导过程略。
还有一种算法叫做正规方程算法。不需要多步梯度下降的情况下,也能解出代价函数 J 的最小
值。实际上在数据量较大的情况下,梯度下降法比正规方程要更适用一些。
(二)多变量线性回归
刚刚我们讨论了单变量特征的回归模型,现在我们对租金模型增加更多的特征,比如楼层数,房间的数量,等,这些因素都是可以对租金的高低产生影响的。与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
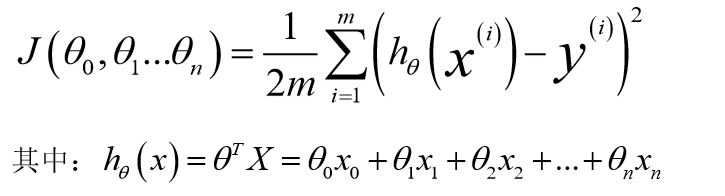
我们的目标和单变量线性回归问题中一样,是要找出使得代价函数最小的一系列参数。
<特征缩放>
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯
度下降算法更快地收敛。
以租金问题为例,假设我们使用两个特征,房间的尺寸和房间的个数,尺寸的值为 0
1000 平方米,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等
高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。
最简单的方法是:
了解了线性回归的这么多理论之后,现在让我们用代码实现一下线性回归吧。
原文地址:http://www.cnblogs.com/xiaojuhere/p/7681005.html