标签:ges 进制 const code eof idt hid isp 它的

题目大意
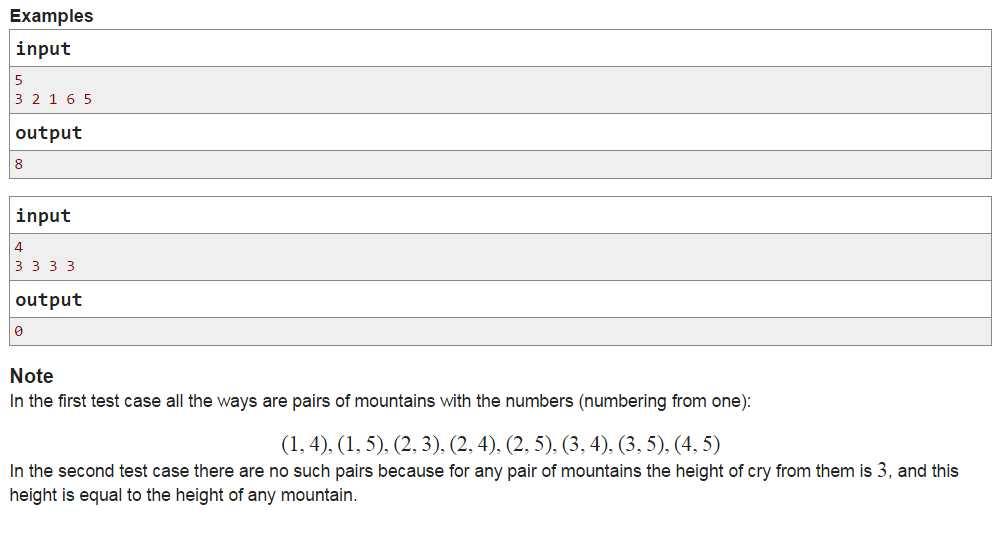
给出一个有n个数的序列
求符合 区间各数或起来的数小于区间最大数 的区间的个数
题解
预处理出每个数每一位是0的那位左边最近的1和右边最近的1,用单调栈找出每个最大值所在的区间的左右端点,统计答案即可。

#include<cstdio> #include<algorithm> #include<cstring> #define LL long long using namespace std; const int maxn=500010,inf=2e9; int n,top,st[maxn],a[maxn],digit[maxn][32],pre[maxn][32],Pre[maxn],next[maxn][32],Next[maxn],cnt[maxn]; LL ans; void read(int &k){ k=0; int f=1; char c=getchar(); while (c<‘0‘||c>‘9‘)c==‘-‘&&(f=-1),c=getchar(); while (‘0‘<=c&&c<=‘9‘)k=k*10+c-‘0‘,c=getchar(); k*=f; } int main(){ read(n); for (int i=1;i<=n;i++){ read(a[i]); for (int x=a[i];x;x>>=1) digit[i][++cnt[i]]=x&1; //处理出a[i]二进制下的每一位 } //////////////////////////////////////////// //pre[i][j]表示:在第j位上,第i个数为0时,左边最近的为1的位置;next[i][j]为右边最近的1的位置 for (int j=1;j<=30;j++){ int last=0; for (int i=1;i<=n;i++) if (!digit[i][j]) pre[i][j]=last; else last=i; } for (int j=1;j<=30;j++){ int first=n+1; for (int i=n;i;i--) if (!digit[i][j]) next[i][j]=first; else first=i; } //////////////////////////////////////////// //对于一个数,不合法区间的左端点为其各个为0数位上,左边最近的1的位置的最大值 //右端点为其各个为0数位上,右边最近的1的位置的最小值 //即对于maxnumber,它的每个为0位,不合法区间内的其他数的这一位都为0,这样区间or起来之后等于maxnumber memset(Next,32,sizeof(Next)); for (int i=1;i<=n;i++) for (int j=1;j<=30;j++) if (!digit[i][j]) Pre[i]=max(Pre[i],pre[i][j]),Next[i]=min(Next[i],next[i][j]); //////////////////////////////////////////// 单调栈维护以a[i]为最大值的区间的左右端点 a[++n]=inf; for (int i=1;i<=n;i++){ for (;top&&a[i]>=a[st[top]];top--){ ans+=1LL*((i-1)-st[top]+1)*(st[top]-(st[top-1]+1)+1); //以a[st[top]]为最大值的全部区间个数 ans-=1LL*(st[top]-max(st[top-1]+1,Pre[st[top]]+1)+1)*(min(i-1,Next[st[top]]-1)-st[top]+1); //减去不合法的区间个数 } st[++top]=i; } printf("%lld\n",ans); return 0; }
标签:ges 进制 const code eof idt hid isp 它的
原文地址:http://www.cnblogs.com/DriverLao/p/7682581.html