LIS&LCS最长上升子序列，最长公共子序列

标签：pos   一个   code   div   bfc   9.png   子串   状态   nbsp   

何为子序列？ 子序列是  从原序列取任意多项 不改变它们的顺序 得到序列

最长上升子序列是： 取出的子序列元素大小从小到大

一个O(N^2)的算法

状态 d[ i ]  表示  以第i个元素为结尾  得到的上升子序列的最大长度

状态转移方程： d[ i ] = d[ j ] +1 (a [ j ] < a[ i]  &&   j < i )

for(int i=0;i<n;i++)
{
    d[i]=1;
    for(int j=0;j<i;j++)
        if(a[j]<a[i]) d[i] = max(d[i] , d[j]+1);
    ans=max(ans, d[i]);
}
//ans 就是最大值

O(Nlogn）的算法

在dp值相同时 保留a值 最小的更好 ，  因为 最小的和后面可以组成上升序列 而其他的未必能 。。

状态 d [ i ] 表示  最长上升子序列的长度为 i 的序列 的末尾值为 d[i]

这个序列的值一定是从小到大有序的//原因在上，用心想想

这样，对于每个需要处理的值，可以快速的查找到该值可以添加到序列的位置　　//二分查找

 1 int len=1;       //len 是最长值    
 2 d[1]=a[1];
 3 for(int i=2;i<=n;i++)
 4 {
 5         if(a[i] > d[len] ) d[++len ] =a[i];
 6         else {
 7             int pos= lower_bound(d , d+len , a[i] ) -d;
 8             d[pos] = a[i];
 9         }
10 }
11 cout<<len<<endl;

LCS 最长公共子序列

给定两个串 a, b 求两个串的最长公共子序列

状态d[ i ] [ j ] 表示 a串前i个字符和b串前j个字符的LCS

状态转移 ：   如果a[i] == b[j]  那么  可以将a[i] 和b[j] 作为子串的末尾 d[ i ] [ j ] = d[ i - 1 ] [ j - 1 ] + 1，也可以不作为结尾 d[ i ] [ j ] =  max( d [ i - 1 ] [ j ] , d [ i ] [ j - 1 ] )

　　　　　　可以证明 max(d [ i -1 ] [ j ] , d[ i ] [ j -1 ])  <= d[ i - 1 ] [ j - 1 ] +1

　　　　　　那么 a [ i ] == b [ j ] 时  d[ i ] [ j ] = d [ i -1 ] [ j - 1] + 1;

　　　　　　如果a [ i ] != b[ j ]    d[ i ] [ j ] =max( d[ i - 1] [ j ] , d [ i ] [ j - 1 ] );

for(int i=0;i<len1;i++)
{
    for(int j=0;j<len2;j++)
    {
        if(a[i]==b[j]) d[i][j]=d[i-1][j-1]+1;
        else d[i][j]=max(d[i-1][j],d[i][j-1]);
    }
}

一个例子

a="abcfbc", b="abfcab"

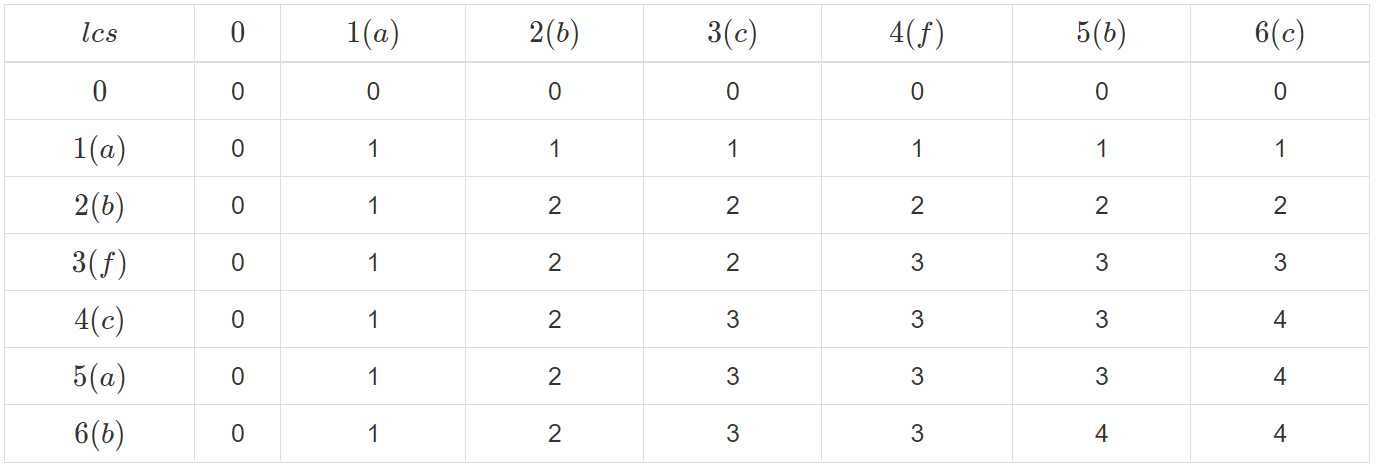
最后的lca[ 6 ] [ 6] 就是最终结果

LIS&LCS最长上升子序列，最长公共子序列

标签：pos   一个   code   div   bfc   9.png   子串   状态   nbsp   

原文地址：http://www.cnblogs.com/star-and-me/p/7683786.html