标签:因此 最小 ima 操作 get 包装 tee sortedmap 结构
TreeMap实现了SortedMap接口,会按照Key的大小顺序对Map中的元素进行排序,Key大小的评判可以通过其本身的自然顺序,也可以通过构造时传入的比较器。
TreeMap底层通过红黑树实现的,也就意味着containKey(),get(),put(),remove()都有着log(n)的时间复杂度。
性能原因,treeMap是非同步的,如果需要在多线程环境中使用,需要程序员手动同步;或者包装成同步的
:SortedMap m = Collections.synchronizedSortedMap(new TreeMap(...))
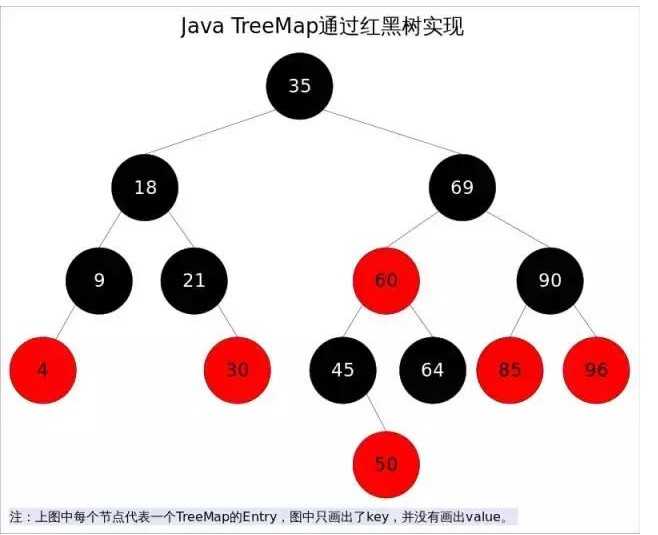
红黑树是一种近似平衡的二叉查找树,它能够确保任何一个节点的左右子树的高度差不会超过二者中的较低那个的一倍。
红黑树满足的条件:
1,每个节点要么是红色,要么是黑色
2,根节点必须是黑色
3,红色节点不能连续,---红色节点的父亲或者孩子必须是黑色
4,对于每个节点,从该点至null---树尾端的任何路径,都含有相同个数的黑色节点。
在树的结构发生改变时,往往会破坏上述条件3或4,需要通过调整使得查找树重新满足红黑树条件。
调整可分为两类:一类是颜色调整,即改变某个节点的颜色;另一类是结构调整,即改变检索树的结构关系。
结构调整过程包含两个基本操作:左旋,右旋。
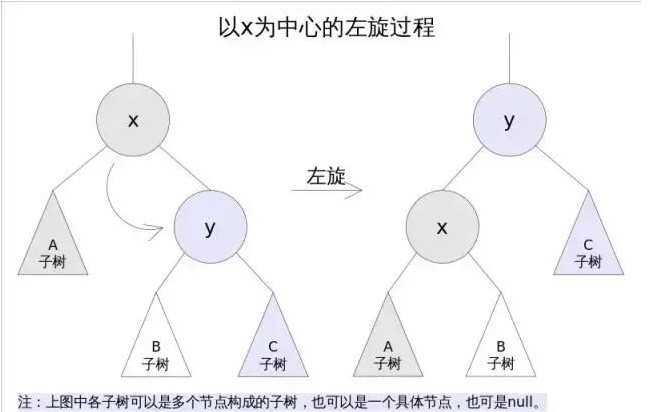
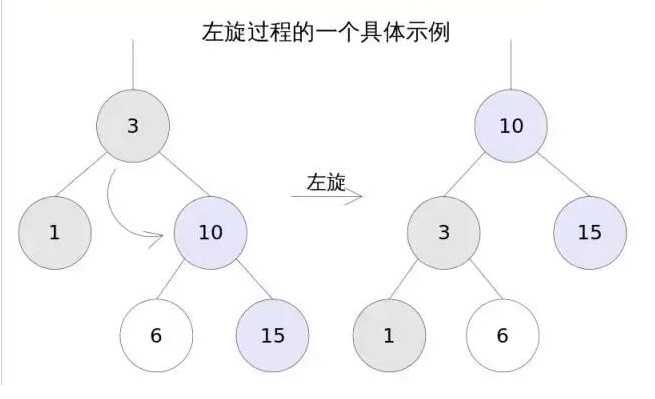
左旋
左旋的过程是将x的右子树绕x逆时针旋转,使得x的右子树成为x的父亲,同时修改相关节点的引用。
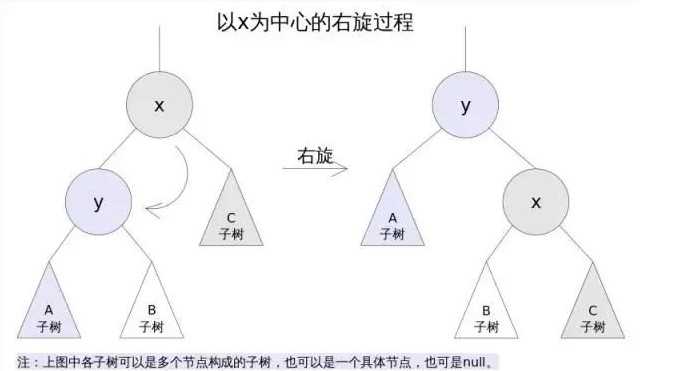
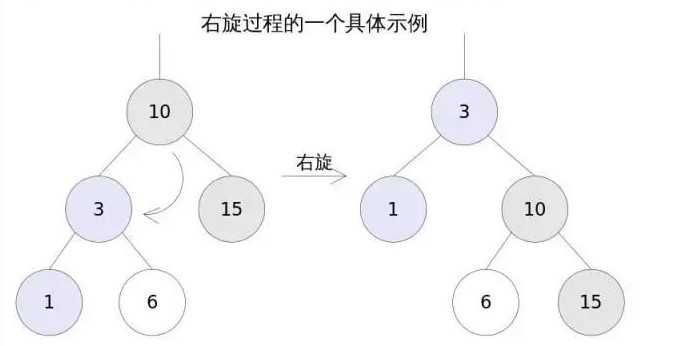
右旋
右旋的过程是将x的左子树绕x顺时针旋转,使得x的左子树成为x的父亲,同时修改相关节点的引用。
方法剖析
get(Key k)
根据指定的key返回对应的value,该方法调用了getEntry(Key k)得到相应的entry,然后返回entry.value。
getEntry是算法的核心,就是根据key的自然顺序或者比较器顺序对二叉查找树进行查找,直到找到满足k.compareTo(p.key) == 0的entry
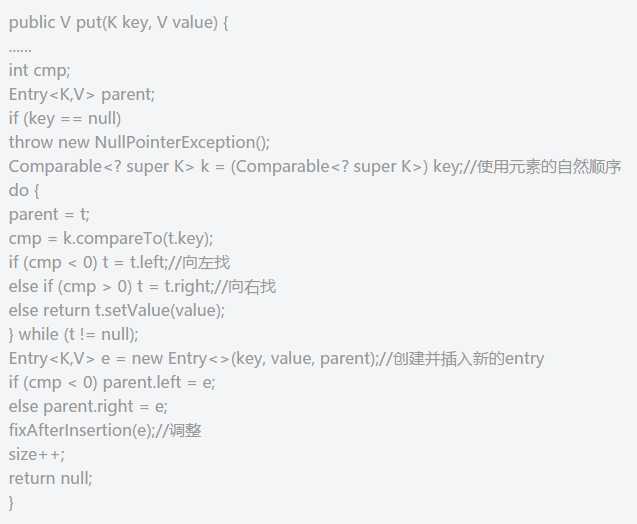
put()
是将指定的key,value对添加到map里。该方法首先会对map进行一次查找,看是否包含该元素,如果包含则直接返回,查找过程类似于getEntry()方法;如果没有找到则会在红黑树中插入新的entry,如果插入之后破坏了红黑树的约束,还需要进行调整---旋转,改变某些节点的颜色。
首先在红黑树找到合适的位置,然后创建新的entry并插入---新插入的节点一定是树的叶子。
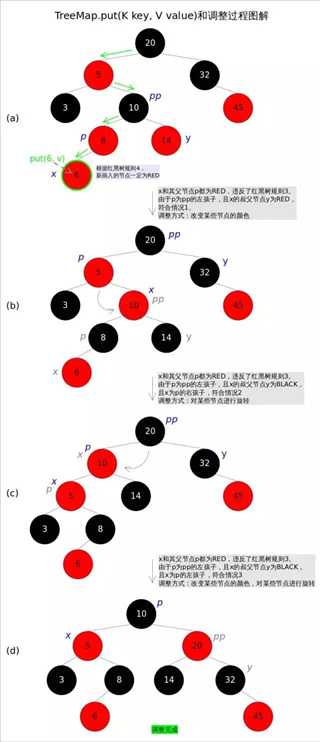
fixAfterInsertion()---调整函数。
remove(key k)
删除key值对应的entry,首先通过getEntry找到key对应的entry,然后调用deleteEntry(entry)删除对应的entry,删除操作会改变红黑树的结构,有可能破坏红黑树的约束,因此有可能要调整。
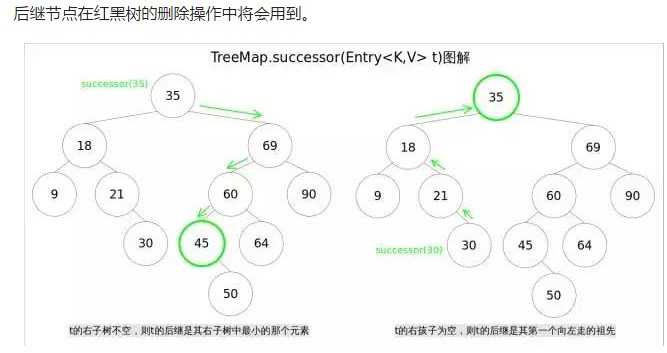
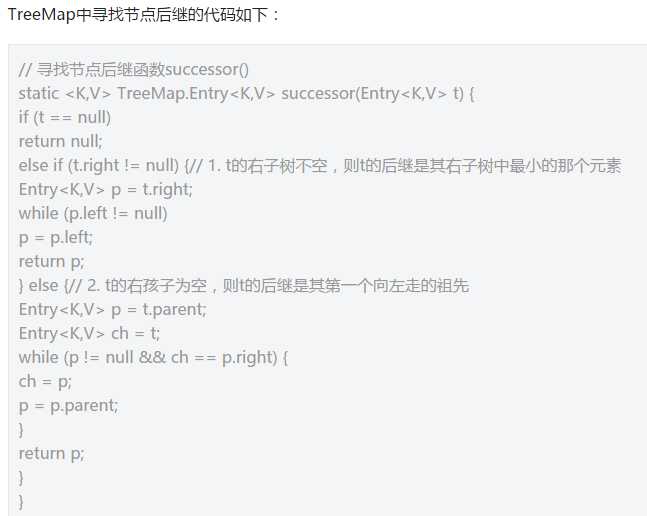
寻找节点后继
对于一颗二叉查找树,给定节点T,其后继--树中大于t的最小的那个元素通过如下方式找到:
1,t的右子树不空,则t的后继是其右子树中最小的那个元素
2,t的右孩子为空,则t的后继是其第一个向左走的祖先
由于红黑树是一颗增强版的二叉查找树,删除操作和普通二叉树删除操作唯一的区别是红黑树在节点删除后可能需要调整。
1,删除节点p的左右子树都为空,或者只有一颗子树为空
2,删除节点p的左右子树非空
对于情况一,直接将p删除(左右子树都为空时),或者用非空子树替代p(只有一颗子树为空);
对于情况二,可以用p的后继s(树中大于x的最小的元素)代替p,然后使用情况1删除s。
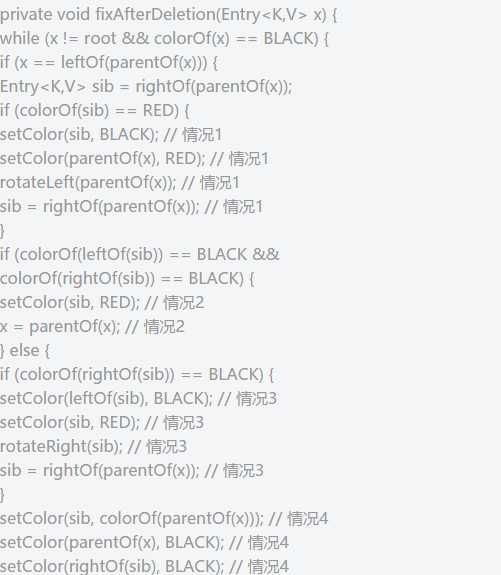
只有删除black的时候,才会触发调整函数fixAfterDeletion,因为删除red不会破坏红黑树的任何约束,而删除black会破坏规则4
TreeSet
TreeSet是对TreeMap的简单包装,对TreeSet的函数调用都会转换成合适的TreeMap方法,因此TreeSet的实现非常简单。
取自:头条---java进阶架构
简单理解红黑树
标签:因此 最小 ima 操作 get 包装 tee sortedmap 结构
原文地址:http://www.cnblogs.com/shangdongbin/p/7699995.html