标签：ora   size   相同   ==   依赖   复杂   阶段   怎样   计算   

 转自：http://blog.csdn.net/qq_30137611/article/details/77655707

初探动态规化

刚学动态规划，或多或少都有一些困惑。今天我们来看看什么是动态规划，以及他的应用。
学过分治方法的人都知道，分治方法是通过组合子问题来求解原问题，而动态规划与分治方法相似，都是通过组合子问题的解来求解原问题，只不过动态规划可以解决子问题重叠的情况,即不同的子问题有公共的子子问题。
说了这么多的比较苦涩的话，只是为了回头再看，我们通过一个例子来具体说明一下：

钢条切割问题

小王刚来到一家公司，他的顶头boss买了一条长度为10的钢条，boss让小王将其切割为短钢条，使得这条钢条的价值最大，小王应该如何做？我们假设切割工序本身没有成本支出。
已知钢条的价格表如下：

小王是一个非常聪明的人，立刻拿了张纸画了一下当这根钢条长度为4的所有切割方案(将问题的规模缩小)

小王很快看出了可以获得的最大收益为5+5=10，他想了想，自己画图以及计算最大值的整个流程，整理了一下：
1>先画出切一刀所有的切割方案：（1+8）、（5+5）、（8+1）一共三种可能，也就是 4 - 1中可能，把这个 4 换成 n（将具体情况换成一般情况）,就变成了长度为 n 的钢条切一刀会有 n -1 中可能，然后在将一刀切过的钢条再进行切割。
同上，（1+8）这个组合会有 2 中切法，（1+1+5）和（1+5+1）【看图】，同理，（5+5）会有两种切法（1+1+5）和（5+1+1）,由于（1+1+5）和上面的（1+1+5）重合，所以算一种切法，依次类推。
由于我们对 n-1个切点总是可以选择切割或不切割，所以长度为 n 的钢条共有 2^(n-1)中不同的切割方案不懂的点我

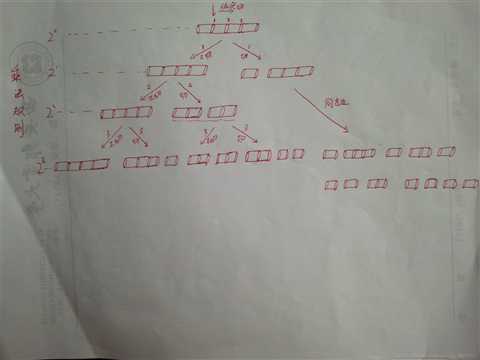
 2>从这2^(n-1)中方案中选出可以获得最大收益的一种方案

学过递归的小王很快就把上述过程抽象成了一个函数，写出了以下的数学表达式：
设钢条长度为n的钢条可以获得的最大收益为 r(n) （n>=1）

第一个参数P(n)表示不切割对应的方案，其他 n-1个参数对应着另外 n-1中方案（对应上面的一刀切）
为了求解规模为 n 的原问题，我们先求解形式完全一样，但规模更小的子问题。即当完成首次切割后，我们将两段钢条看成两个独立的钢条切割问题来对待。我们通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的最优解我们成钢条问题满足最优子结构性质
编程能力很强的小王拿出笔记本
很快的在电脑上写下了如下代码

#include <stdio.h>

int CUT_ROD(int * p ,int n);
int max(int q, int a);

int main(void){
    int i = 0;
    int p[10] = {1,5,8,9,10,17,17,20,24,30};
    printf("请输入钢条的长度(正整数):\n");
    scanf("%d",&i);

    int maxEarning = CUT_ROD(p,i); // 切割钢条
    printf("钢条长度为 %d 的钢条所能获得的最大收益为:%d\n",i,maxEarning);

    return 0;
}
// 切割钢条
int CUT_ROD(int * p,int n){
    int i;
    if(n < 0){
        printf("您输入的数据不合法！\n");
        return -1;
    }else if(n == 0){
        return 0;
    }else if(n > 10){
        printf("您输入的值过大！\n");
        return -1;
    }
    int q = -1;
    for(i = 0; i < n;i++){
        q = max(q,p[i] + CUT_ROD(p,n-1-i));
    }
    return q;
}

int max(int q, int a){
    if(q > a)
        return q;
    return a;
}

沾沾自喜的小王拿着自己的代码到boss面前，说已经搞定了。boss看了看他的代码，微微一笑，说，你学过指数爆炸没，你算算你的程序的时间复杂度是多少，看看还能不能进行优化？小王一听蒙了，自己这些还没有想过，自己拿着笔和纸算了好大一会，得出了复杂度为T(n) = 2^n,没想到自己写的代码这么烂，规模稍微变大就不行了。boss看了看小王，说：你想想你的代码效率为什么差？小王想了想，说道：“我的函数CUT-ROD反复地利用相同的参数值对自身进行递归调用，它反复求解了相同的子问题了”boss说：“还不错嘛？知道问题出在哪里了，那你怎样解决呢？”小王摇了摇头，boss说：“你应该听过动态规划吧,你可以用数组把你对子问题求解的值存起来，后面如果要求解相同的子问题，直接用之前的值就可以了，动态规划方法是付出额外的内存空间来节省计算时间，是典型的时空权衡”，听到这里小王暗自佩服眼前的boss，姜还是老的辣呀。
boss说完拿起小王的笔记本，写下了如下代码：

// 带备忘的自顶向下法 求解最优钢条切割问题
#include <stdio.h>

int MEMOIZED_CUT_ROD(int * p,int n);
int MEMOIZED_CUT_ROD_AUX(int * p, int n, int * r);
int max(int q,int s);

int main(void){
    int n;
    int p[11]={-1,1,5,8,9,10,17,17,20,24,30};
    printf("请输入钢条的长度（正整数 < 10）:\n");
    scanf("%d",&n);
    if(n < 0 || n >10){
        printf("您输入的值有误！");
    }else{
        int r = MEMOIZED_CUT_ROD(p,n);
        printf("长度为%d的钢条所能获得的最大收益为:%d\n",n,r);
    }
    return 0;
}

int MEMOIZED_CUT_ROD(int * p, int n){
    int r[20];
    for(int i = 0; i <= n; i++){
        r[i] = -1; 
    }
    return MEMOIZED_CUT_ROD_AUX(p,n,r); 
}

int MEMOIZED_CUT_ROD_AUX(int * p, int n, int * r){
    if(r[n] >= 0){
        return r[n];
    }
    if(n == 0){
        return 0;
    }else{
        int q = -1;
        for(int i = 1; i <= n; i++){// 切割钢条， 大纲有 n 中方案
            q = max(q,p[i] + MEMOIZED_CUT_ROD_AUX(p,n-i,r));  
        }
        r[n] = q;// 备忘
        return q;
    }
}

int max(int q, int s){
    if(q > s){
        return q;
    }
    return s;
}

小王两眼瞪的直直的。boss好厉害，我这刚入职的小白还得好好修炼呀。
写完boss说：这中方法被称为带备忘的自顶向下法。这个方法按自然的递归形式编写过程，但过程会保存每个子问题的解（通常保存在一个数组或散列表中），当需要一个子问题的解时，过程首先检查是否已经保存过此解，如果是，则直接返回保存的值。还有一种自底向上法。这种方法一般需要恰当定义子问题的规模，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因而我们可以将子问题按规模排序，按由小至大的顺序进行求解，当求解某个子问题是，它所依赖的那些更小的子问题都已经求解完毕，结果已经保存，每个子问题只需求解一次。如果你有兴趣回去好好看看书自己下去好好研究下吧。
最后再考考你，我写的这个带备忘的自顶向下法的时间复杂度是多少？小王看了看代码，又是循环，又是递归的，脑子都转晕了。boss接着说：“你可以这样想，我这个函数是不是对规模为0，1，…，n的问题进行了求解，那么你看，当我求解规模为n的子问题时，for循环是不是迭代了n次，因为在我整个n规模的体系中，每个子问题只求解一次，也就是说我for循环里的递归直接返回的是之前已经计算了的值，比如说 求解 n =3的时候，for(int i = 1,i <=3;i++)，循环体执行三次，n=4时，循环体执行四次，所以说，我这个函数MEMOIZED_CUT_ROD进行的所有递归调用执行此for循环的迭代次数是一个等差数列，其和是O(n^2)”,是不是效率高了许多。小王嗯嗯直点头，想着回去得买本《算法导论》好好看看。

无后效性是一个问题可以用动态规划求解的标志之一，理解无后效性对求解动态规划类题目非常重要

转自：http://blog.csdn.net/qq_30137611/article/details/77655707

某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响

百度百科是这样定义的，是不是很苦涩，难懂。并且网上对这个名词的解释大多都是理论性的，不好理解，今天我们通过一个例子来看看什么是无后效性

现在有一个四乘四的网格，左上角有一个棋子，棋子每次只能往下走或者往右走，现在要让棋子走到右下角

假设棋子走到了第二行第三列，记为s(2,3),如下图，画了两条路线和一条不符合题意的路线，那么当前的棋子[s(2,3)位置]怎么走到右下角和之前棋子是如何走到s(2,3)这个位置无关[不管是黑色尖头的路线还是蓝色箭头的路线]

换句话说，当位于s(2,3)的棋子要进行决策（向右或者向下走）的时候，之前棋子是如何走到s(2,3)这个位置的是不会影响我做这个决策的。之前的决策不会影响了未来的决策（之前和未来相对于现在棋子位于s(2,3)的时刻），这就是无后效性,也就是所谓的“未来与过去无关”

看完了无后效性，那我们再来看看有后效性，还是刚才的例子，只不过现在题目的条件变了，现在棋子可以上下左右走但是不能走重复的格子

那么现在红色箭头就是一个合法的路线了，当我的棋子走到了s(2,3)这个位置的时候，要进行下一步的决策的时候，这时候的决策是受之前棋子是如何走到s(2,3)的决策的影响的，比如说红色箭头的路线，如果是红色箭头决策而形成的路线，那么我下一步决策就不能往下走了[因为题意要求不能走重复的格子]，之前的决策影响了未来的决策，”之前影响了未来”,这就叫做有后效性

在此感谢腾讯大神的指导，学习离不开自己的努力和名师的指导。

动态规划初探及什么是无后效性？ （转）

标签：ora   size   相同   ==   依赖   复杂   阶段   怎样   计算   

原文地址：http://www.cnblogs.com/mhpp/p/7700235.html