标签:com log display ems ons space col get line
题面在最下方。
首先最短路判断一下有没有输出 -1 的情况。
然后把握答案可以二分求解的特点,那就很容易解决了。
令边中最大的年代为 maxx
那么就在[1,maxx]中进行二分求解,枚举年代mid,跑一遍最短路,不走年代<=mid的边,然后判断dis[n]是否>=T,如果>=说明mid可能偏大,否则mid可能偏小。
怎么优化?
把所有边的年代存下来,sort一次,然后在这些数据里面二分(mid只能是出现过的年代)。
优化你的最短路算法,例如SPFA的LLL优化与SLF优化

二分暴力求解即可。

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 template<class T> inline void read(T &_a){ 6 int _ch=getchar();_a=0; 7 while(_ch<‘0‘ || _ch>‘9‘)_ch=getchar(); 8 while(_ch>=‘0‘ && _ch<=‘9‘){_a=(_a<<1)+(_a<<3)+_ch-‘0‘;_ch=getchar();} 9 } 10 11 const int maxn=20001,maxm=100001; 12 int n,m,T,egcnt,head[maxn],q[maxn],dis2[maxn],dis[maxn],tail,h,maxx; 13 bool ins[maxn],vis[maxn]; 14 struct edge{ 15 int next,to,dis,year; 16 }w[maxm<<1]; 17 18 inline void addedge(int from,int to,int dis,int year) 19 { 20 w[++egcnt].dis=dis; 21 w[egcnt].to=to; 22 w[egcnt].year=year; 23 w[egcnt].next=head[from]; 24 maxx=max(maxx,year); 25 head[from]=egcnt; 26 } 27 28 inline void spfa(int y){ 29 memset(dis,0x7f,sizeof(dis)); 30 dis[1]=0; q[1]=1; h=0; tail=1; 31 while(h!=tail) 32 { 33 h=h%20000+1; 34 int now=q[h]; 35 ins[now]=false; 36 for (register int i=head[now];i;i=w[i].next) 37 if(w[i].year>y){ 38 if(dis[w[i].to]>dis[now]+w[i].dis) 39 { 40 dis[w[i].to]=dis[now]+w[i].dis; 41 if(!ins[w[i].to]) 42 { 43 ins[w[i].to]=true; 44 tail=tail%20000+1; 45 q[tail]=w[i].to; 46 } 47 } 48 } 49 } 50 } 51 52 int main() 53 { 54 read(n); read(m); read(T); 55 for (register int i=1,s,t,l,y;i<=m;++i) read(s),read(t),read(l),read(y),addedge(s,t,l,y); 56 spfa(0); 57 if(dis[n]>=T) { printf("-1 %d",dis[n]); return 0; } 58 int l=1,r=maxx; 59 while(l<=r) 60 { 61 memset(vis,0,sizeof(vis)); 62 int mid=l+r>>1; 63 spfa(mid); 64 if(dis[n]<T) l=mid+1; 65 else r=mid-1; 66 } 67 printf("%d",r+1); 68 return 0; 69 }
【题目描述】由于A学校生物实验室里那个不负责的数据分析员,实验室的病毒威力被错误估算,导致了可怕的病毒泄漏,现在病毒即将在校园内传播开来。校园里一共有n个建筑物,生物实验室总是位于一号建筑物且在0时刻受到病毒入侵。这n个建筑物由m条单向道路相连(也有可能有建筑物被孤立)。每条道路有两个信息:它的长度,它是多少年前修建的。当一个建筑物被病毒入侵,从被入侵的时刻起,病毒会从所有由这个建筑物通向其他建筑物的道路按着这条道路的方向以1个单位每秒的速度行进。校长得知这个事情后,决定放弃这个学校逃跑。校长总是位于编号为n的行政楼,从零时刻开始需要共T秒来逃出行政楼,且逃出行政楼即视为逃出了这个学校。也就是说,如果病毒入侵行政楼的时间不小于T,则校长能够成功逃离。有些时候,校长没有足够的时间逃离,因为病毒到达行政楼的时间太快了。为了让校长能够逃离学校,不得不拆除校园内的一些道路以延缓行政楼的被入侵时间(拆除道路视为在0时刻被拆的道路全部消失)。当然,如果使得病毒根本无法到达行政楼,也是可以的。但是,拆除道路会影响学校的历史气息,且破坏程度定义为拆除的道路中最古老的一条的年龄。请求出保证校长能够安全撤离的情况下,最小的破坏程度。
【输入格式】第一行包含三个整数:n,m,T。接下来m行,每行描述一条有向道路。每行4个整数,si,ti,Li,Yi,分别表示这条道路的起点,终点,长度,这条道路的年龄。
【输出格式】如果不需要拆除任何道路,输出一行两个数:-1和行政楼的被感染时刻(当然这个时刻大于等于T),以空格隔开。否则输出一行包含一个数:最小的破坏程度。
【输入样例一】
5515
12635
24840
13645
34325
45550
【输出样例一】
25
【样例解释一】
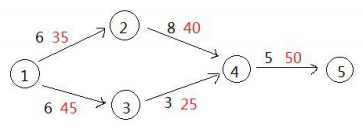
每条边上的黑字对应这条路的长度,红字对应年龄。校长将在第15秒逃出学校,如果不拆除任何道路,行政楼将在第14秒受到入侵。你可以拆除4到5的道路,使得行政楼免于入侵,这样的破坏程度是50。但是最好的方法是拆掉3到4之间的道路,这样使得行政楼在第19秒受到入侵,校长就可以逃离了。
【输入样例二】
3 2 10
1 2 5 30
2 3 6 50
【输出样例二】
-1 11
【数据范围】
对于 60%的数据,n,m<=100.
对于 100%的数据,n<=20000, m<=100000. 数据保证在不拆除任何道路的情况下,从 1 号楼到 n 号楼一定存在路径。
标签:com log display ems ons space col get line
原文地址:http://www.cnblogs.com/jaywang/p/7707210.html