给定一棵无根树,边权都是1,请去掉一条边并加上一条新边,定义直径为最远的两个点的距离,请输出所有可能的新树的直径的最小值和最大值
标签:head 端点 name 表示 turn output 最小 style modern
给定一棵无根树,边权都是1,请去掉一条边并加上一条新边,定义直径为最远的两个点的距离,请输出所有可能的新树的直径的最小值和最大值
第一行包含一个正整数n(3<=n<=500000),表示这棵树的点数。
接下来n-1行,每行包含两个正整数u,v(1<=u,v<=n),表示u与v之间有一条边。
第一行输出五个正整数k,x1,y1,x2,y2,其中k表示新树直径的最小值,x1,y1表示这种情况下要去掉的边的两端点,x2,y2表示这种情况下要加上的边的两端点。
第二行输出五个正整数k,x1,y1,x2,y2,其中k表示新树直径的最大值,x1,y1表示这种情况下要去掉的边的两端点,x2,y2表示这种情况下要加上的边的两端点。
若有多组最优解,输出任意一组。
题解:显然,如果我们已经知道了要切哪条边,得到两棵新树,那么新的直径的最小值就是将两棵树的直径中点连起来,最大值就是将两个直径首尾相连。然后我们将原树的直径拎出来,那么就有以下几种切法:
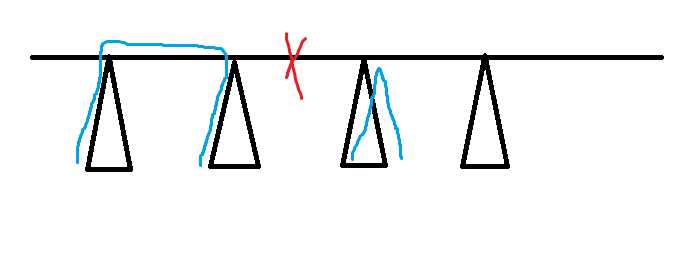
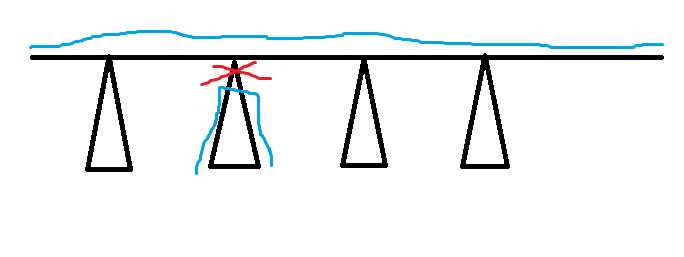
红色代表切割线,蓝色代表新的直径。
然后维护一大坨东西xjb讨论即可,我已无力解释~
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn=500010;
int n,m,cnt,rt;
int to[maxn<<1],next[maxn<<1],head[maxn],dep[maxn],p[maxn],fa[maxn],r1[maxn],r2[maxn],r3[maxn],r4[maxn];
int y1[maxn],y2[maxn],x1[maxn],x2[maxn],v1[maxn],v2[maxn],s1[maxn],s2[maxn];
int ans1,ans2;
inline int rd()
{
int ret=0,f=1; char gc=getchar();
while(gc<‘0‘||gc>‘9‘) {if(gc==‘-‘) f=-f; gc=getchar();}
while(gc>=‘0‘&&gc<=‘9‘) ret=ret*10+gc-‘0‘,gc=getchar();
return ret*f;
}
inline void add(int a,int b)
{
to[cnt]=b,next[cnt]=head[a],head[a]=cnt++;
}
void dfs(int x)
{
if(dep[x]>dep[rt]) rt=x;
for(int i=head[x];i!=-1;i=next[i]) if(!dep[to[i]]) dep[to[i]]=dep[x]+1,fa[to[i]]=x,dfs(to[i]);
}
inline int C1(int x)
{
if(x==1) return -1;
return x+s1[x]-x1[x-1]+s1[x1[x-1]];
}
inline int C2(int x)
{
if(x==m) return -1;
return s1[x]-x+s1[x2[x+1]]+x2[x+1];
}
inline int getmid(int x,int y)
{
memset(dep,0,sizeof(dep));
dep[x]=1,fa[x]=0,dfs(x);
int i,z;
for(i=1,z=y;i<=dep[y]/2;i++,z=fa[z]);
return z;
}
int main()
{
n=rd();
int i,j,a,b;
memset(head,-1,sizeof(head));
for(i=1;i<n;i++) a=rd(),b=rd(),add(a,b),add(b,a);
rt=dep[1]=1,dfs(rt),a=rt;
memset(dep,0,sizeof(dep));
dep[rt]=1,fa[rt]=0,dfs(rt),b=rt;
memset(dep,0,sizeof(dep));
for(i=b;i;i=fa[i]) p[++m]=i,dep[i]=1;
for(i=1;i<=m;i++) rt=p[i],dfs(rt),r1[i]=rt,s1[i]=dep[rt]-1;
memset(dep,0,sizeof(dep));
for(i=1;i<=m;i++) dep[p[i]]=1;
for(i=1;i<=m;i++) dep[p[i]]=0,rt=r1[i],dep[rt]=1,dfs(rt),r2[i]=rt,s2[i]=dep[rt]-1;
s1[0]=s1[m+1]=-1<<30;
for(i=1;i<=m;i++) x1[i]=(s1[i]-i>=s1[x1[i-1]]-x1[i-1])?i:x1[i-1];
for(i=m;i>=1;i--) x2[i]=(s1[i]+i>=s1[x2[i+1]]+x2[i+1])?i:x2[i+1];
for(i=1;i<=m;i++) y1[i]=s2[i]>=s2[y1[i-1]]?i:y1[i-1];
for(i=m;i>=1;i--) y2[i]=s2[i]>=s2[y2[i+1]]?i:y2[i+1];
v1[1]=1,v2[m]=m;
for(i=2;i<=m;i++) v1[i]=C1(i)>=C1(v1[i-1])?i:v1[i-1];
for(i=m-1;i>=1;i--) v2[i]=C2(i)>=C2(v2[i+1])?i:v2[i+1];
ans2=1<<30;
for(i=1;i<m;i++)
{
a=max(C1(v1[i]),s2[y1[i]]),b=max(C2(v2[i+1]),s2[y2[i+1]]);
ans1=max(ans1,a+b+1);
ans2=min(ans2,max(max(a,b),(a+1)/2+(b+1)/2+1));
}
memset(dep,0,sizeof(dep));
for(i=1;i<=m;i++) dep[p[i]]=1;
for(i=1;i<=m;i++)
{
for(j=head[p[i]];j!=-1;j=next[j]) if(!dep[to[j]])
rt=to[j],dep[rt]=1,dfs(rt),r3[to[j]]=rt;
}
memset(dep,0,sizeof(dep));
for(i=1;i<=m;i++) dep[p[i]]=1;
for(i=1;i<=m;i++)
{
for(j=head[p[i]];j!=-1;j=next[j]) if(!dep[to[j]])
rt=r3[to[j]],dep[rt]=1,dfs(rt),r4[to[j]]=rt,ans1=max(ans1,dep[rt]+m-1);
}
printf("%d ",ans2);
for(i=1;i<m;i++)
{
a=max(C1(v1[i]),s2[y1[i]]),b=max(C2(v2[i+1]),s2[y2[i+1]]);
if(ans2==max(max(a,b),(a+1)/2+(b+1)/2+1))
{
printf("%d %d ",p[i],p[i+1]);
if(C1(v1[i])>s2[y1[i]]) printf("%d ",getmid(r1[v1[i]],r1[x1[v1[i]-1]]));
else printf("%d ",getmid(r1[y1[i]],r2[y1[i]]));
if(C2(v2[i+1])>s2[y2[i+1]]) printf("%d\n",getmid(r1[v2[i+1]],r1[x2[v2[i+1]+1]]));
else printf("%d\n",getmid(r1[y2[i+1]],r2[y2[i+1]]));
break;
}
}
printf("%d ",ans1);
for(i=1;i<m;i++)
{
a=max(C1(v1[i]),s2[y1[i]]),b=max(C2(v2[i+1]),s2[y2[i+1]]);
if(ans1==a+b+1)
{
printf("%d %d ",p[i],p[i+1]);
if(C1(v1[i])>s2[y1[i]]) printf("%d ",r1[v1[i]]);
else printf("%d ",r1[y1[i]]);
if(C2(v2[i+1])>s2[y2[i+1]]) printf("%d\n",r1[v2[i+1]]);
else printf("%d\n",r1[y2[i+1]]);
return 0;
}
}
memset(dep,0,sizeof(dep));
for(i=1;i<=m;i++) dep[p[i]]=1;
for(i=1;i<=m;i++)
{
for(j=head[p[i]];j!=-1;j=next[j]) if(!dep[to[j]])
{
rt=r3[to[j]],dep[rt]=1,dfs(rt),r4[to[j]]=rt;
if(ans1==dep[rt]+m-1)
{
printf("%d %d %d %d\n",p[i],to[j],p[1],rt);
return 0;
}
}
}
}//6 1 2 2 3 2 4 4 5 6 5
【BZOJ4379】[POI2015]Modernizacja autostrady 树形DP
标签:head 端点 name 表示 turn output 最小 style modern
原文地址:http://www.cnblogs.com/CQzhangyu/p/7707874.html