标签:image 算法 概念 特殊 graph .com es2017 this 有向图
前向星是一种特殊的边集数组,我们把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序,
并记录下以某个点为起点的所有边在数组中的起始位置和存储长度,那么前向星就构造好了.
用len[i]来记录所有以i为起点的边在数组中的存储长度.
用head[i]记录以i为边集在数组中的第一个存储位置.
先举个例子吧,给一个有向图,读入各边的起点和终点
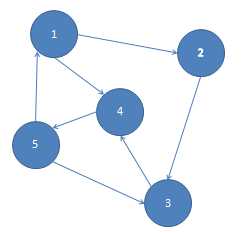
边数:7
起点 终点
1 2
2 3
3 4
1 4
4 5
5 1
5 3
我们先把边集数组中的每一条边按照起点从小到大排序,如果起点相同就按照终点从小到大排序
排序后得到:
1: 1 2
2: 1 4
3: 2 3
4: 3 4
5: 4 5
6: 5 1
7: 5 3
然后我们用len,head数组进行存储操作
head[1]=1,len[1]=2
head[2]=3,len[2]=1
head[3]=4,len[3]=1
head[4]=5,len[4]=1
head[5]=6,len[5]=2
这样的储存方式很直观,一般的新手都喜欢用
但是利用前向星会有排序操作,如果用快排时间至少为O(nlog(n))
这时候我们就需要引入一个更加优秀的算法——链式前向星
由于在很多图论算法中都要用到链式前向星的存储方式,所以正确深入地理解链式前向星是每一个OIer都应该做到的
先来看看代码
先建个结构体
struct Edge{ int next,to; int w;//this is the weight of each edge }edge[M+5];//M is the total_number of the graph_edges
其中edge[i].to表示第i条边的终点,edge[i].next表示与第i条边同起点的下一条边的存储位置,edge[i].w为边权值.
然后再加一个head数组,用head[i]记录以i为边集在数组中的最后一个存储位置.
int head[M];//M is the total_number of the graph_edges
有了结构体,我们该如何建边呢,别着急,先放上代码
int cnt=0; void add(int u,int v,int w){ edge[cnt].to=v;edge[cnt].w=w;edge[cnt].next=head[u];head[u]=cnt++; }
很明显,head[i]保存的是以i为起点的所有边中编号最大的那个,而把这个当作顶点i的第一条起始边的位置.
这样在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性.
建好了边,我们又改如何遍历呢
for(int u=1;u<=n;u++)//n is the total_number of points for(int i=head[u];~i;i=edge[i].next)
至此,基础概念的讲解就结束了
标签:image 算法 概念 特殊 graph .com es2017 this 有向图
原文地址:http://www.cnblogs.com/muzu/p/7709632.html