标签：矩阵 2-2 基础上 开始 新规 .com 机器 mda 额外
一、纲要
欠拟合和过拟合
代价函数正则化
正则化线性回归
正则化逻辑回归
二、内容详述
1、欠拟合和过拟合
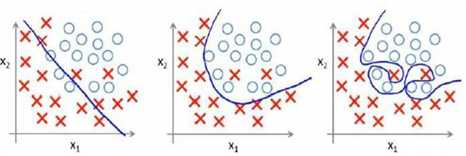
欠拟合，也叫高偏差，就是没有很好的拟合数据集的情况。如下图中的左图所示
过拟合，也叫高方差，就是虽然高阶多项式可以完美的拟合所有的数据，但会导致函数过于庞大，变量太多而我们又没有足够的数据来约束这个模型，这就是过度拟合。过度拟合的原因，简单来说就是过多的特征变量和过少的数据集。如下图右。
过拟合带来的效果就是，虽然可以完美的拟合现有的数据集，但是在预测新数据方面却表现的不尽如人意。所以最适合的还是中间的方式。
当然上面是线性回归的过拟合问题，逻辑回归中也存在这样的问题，就以多项式理解，阶数越高，拟合程度越好，但是预测方面就表现的很差。那么如何解决这些问题呢？这里就要引入“正则化”的概念！
2、代价函数正则化
以第一个问题中的线性回归过拟合为例，我们应该怎样用正则化解决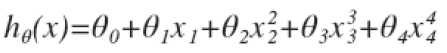
这个问题呢？我们知道如果让高次项系数为0的话，我们就可以比较好的进行拟合。所以我们假设代价函数是
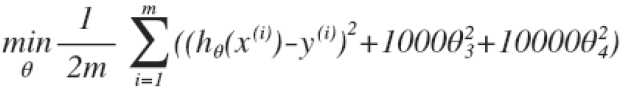，然后在求解代价函数J最小化的
过程中我们就会使Θ3、Θ4尽可能的小，这样的话高次项就趋于0，就能很好的解决这个问题。这就给了我们正则化算法的启示。
我们在代价函数J后面加入一个正则项，代价函数就变为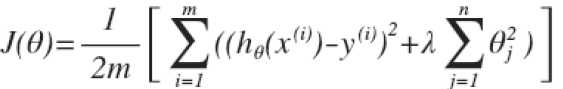
，其中λ为正则化参数。需要注意的是，这里的正则项Θ的Θj是从j=1开始到j=n为止，而不包括Θ0，虽然加与不加Θ0的结果相差不大，但是按照惯例一般Θ0单独考虑。所以我们在使用梯度算法的时候Θ0的参数更新要与其他Θj分开考虑。
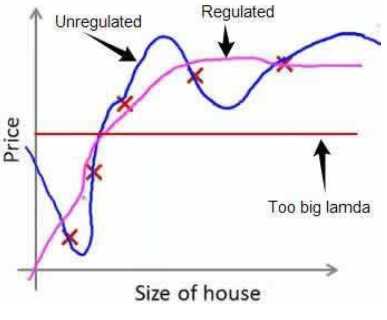
这里需要强调的一点是，正则化参数的选择非常重要，如果λ过大，那么就会使得Θj(j=1,2,3...n)都基本趋于0，也就是只剩下hθ(x)=θ0，就如下图的情况，这样就变成了欠拟合的问题(Too big lamda)，而当λ选择合适的话，过拟合的曲线(Unregulated)就会变成良好的Regulated
3、正则化线性回归
正则化线性回归的代价函数J为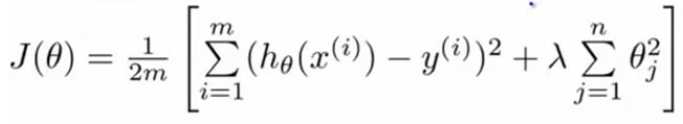
，在使用梯度下降法之前需要对J进行偏导，
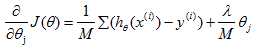，然后带入梯度下降法得到：
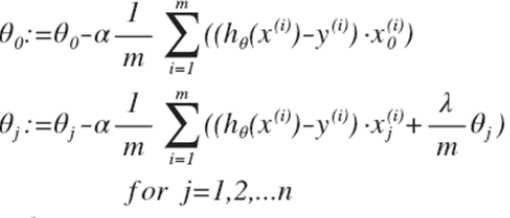，之前说过这里Θ0的参数更新要与其他Θj分开考虑的原因。对θj进行调整得到
，这个式子是不是很熟悉？跟之前的梯度下降法参数更新公式很像，区别只是θj变成了θj(1-α*(λ/m))，这里1-α*(λ/m)就是一个小于1的常数，可能是0.99或0.98.这里可以看出正则化线性回归的梯度下降算法的变化在于，每次都在原有的更新规则的基础上令θ额外减去一个值。
之前我们说的线性回归还有一种正规方程解法，我们同样可以对线性回归正规方程进行正则化，方法为
X = [(x(0))T (x(1))T (x(2))T ... (x(n))T]T，y=[y(1) y(2) y(3) ... y(m)]T，X是m*(n+1)维矩阵，y为m*1维矩阵
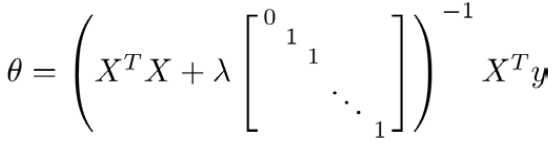图中矩阵的尺寸为(n+1)*(n+1)
4、正则化逻辑回归
代价函数为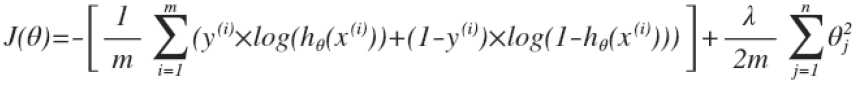
，用梯度下降法进行参数更新得到的方程为：
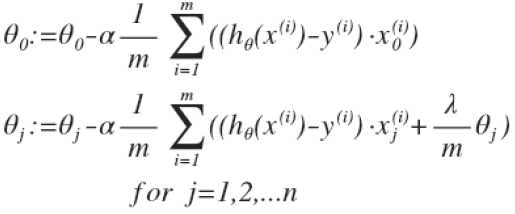这里虽然形式跟线性回归的梯度下降法一样，但是由于hθ(x)的不同，所以两者还是有很大差别
标签：矩阵 2-2 基础上 开始 新规 .com 机器 mda 额外
原文地址：http://www.cnblogs.com/kl2blog/p/7712210.html
