标签:image 除了 优化 文件 最大费用最大流 加工 .com stream char
问题描述
在《Harry Potter and the Chamber of Secrets》中,Ron 的魔杖因为坐他老爸的 Flying Car 撞到了打人柳,不幸被打断了,从此之后,他的魔杖的魔力就大大减少,甚至没办法执行他施的魔咒,这为 Ron 带来了不少的烦恼。这天上魔药课,Snape 要他们每人配置一种魔药(不一定是一样的),Ron 因为魔杖的问题,不能完成这个任务,他请 Harry 在魔药课上(自然是躲过了 Snape 的检查)帮他配置。现在 Harry 面前有两个坩埚,有许多种药材要放进坩埚里,但坩埚的能力有限,无法同时配置所有的药材。一个坩埚相同时间内只能加工一种药材,但是不一定每一种药材都要加进坩埚里。加工每种药材都有必须在一个起始时间和结束时间内完成(起始时间所在的那一刻和结束时间所在的那一刻也算在完成时间内),每种药材都有一个加工后的药效。现在要求的就是 Harry 可以得到最大的药效。
输入
输入文件的第一行有 2 个整数,一节魔药课的 t(1≤t<≤500)和药材数 n(1≤n≤100)。
输入文件第 2 行到 n+1 行中每行有 3 个数字,分别为加工第 i 种药材的起始时间 t1、结束时间 t2、(1≤t1≤t2≤t)和药效 w(1≤w≤100)。
输出
输出文件 medic.out 只有一行,只输出一个正整数,即为最大药效。
输入样例
7 4
1 2 10
4 7 20
1 3 2
3 7 3
输出样例
35
注释
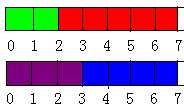
本题的样例是这样实现的:第一个坩埚放第 1、4 种药材,第二个坩埚放第
2、3 种药材。这样最大的药效就为 10+20+2+3=35。
如图,数字为时间轴。
数据规模
对于 30%的数据
1<=t<=500
1<=n<=15
1<=w<=100
1<=t1<=t2<=t
对于 100%的数据
1<=t<=500
1<=n<=100
1<=w<=100
1<=t1<=t2<=t
分析
这道题我和std写的不太一样,std用的是DP,而我太弱了,只会写一个费用流...
一、STD的DP
看完题目后,对题目分析可知,此题的最优解法就是动态规划。[???]
当然,因为有两个坩锅,所以明显是一道双进程动态规划题目。因此,先用动态规划求解一个坩锅能达到的最大药效,把已用的药材去掉,再次动态规划的方法是不可行的!
1.分析最优子结构:
数据备注:
t1[i]表示第i种药材的起始时间
t2[i]表示第i种药材的结束时间
w[i]表示第i种药材的药效
time表示总时间 n表示药材总数
(为了让大家更好理解 先讲一种未优化的算法)
设动态规划数组 dp[i][j][k] 表示前i种药材放入两个坩锅,第一个坩锅达到时间j,第二个坩锅达到k时所能达到的最大药效。题目的解就是dp[n][time][time];
因为要知道在time时刻两个坩锅的效益和,则需要用到它的子结构的最优值。
分析子结构的最优值的取得条件:
对于第i种药材,放入两个坩锅,有三种处理方法:
1. 把它放入第一个坩锅;
2. 把它放入第二个坩锅;
3. 不放入任何坩锅
对1:
dp[i][j][k]=dp[i-1][t1[i]-1][k]+w[i]; 条件:仅当j=t2[i];
对2:
dp[i][j][k]=dp[i-1][j][t1[i]-1]+w[i]; 条件:仅当k=t2[i];
对3:
dp[i][j][k]=max{ dp[i-1][j][k], 无条件
dp[i][j-1][k], 条件 j>0
dp[i][j][k-1], 条件 k>0
因此 子结构dp[i][j][k]的取值就是对1,2,3种状态的最大值
即:
dp[i][j][k]=max{
dp[i-1][t1[i]-1][k]+w[i]; 条件:仅当j=t2[i];
dp[i-1][j][t1[i]-1]+w[i]; 条件:仅当k=t2[i];
dp[i-1][j][k], 无条件
dp[i][j-1][k], 条件 j>0
dp[i][j][k-1], 条件 k>0
}
2.解决后效性:
为了解决后效性,在这里,当且仅当j=t1[i]或k=t1[i]时,药材才会被放入坩锅内,且保证了同一种药品不会在以后被多次放入或者是同时放入二个坩锅,当然,仅仅是这样还是不能保证能求出最优解,因为在计算过程中,结构会被刷新,因此对于结束时间较晚的药材,若在结束时间较前的药材先被计算,则较前的药材就以为价值小而不会被记录,因此就应该在动态规划之前将数据按结束时间t2[i]升序排序。因此,我们完美的消除了后效性。
3.优化问题:
1.时间复杂度的优化:
根据对称性,两个坩锅不计先后,且一摸一样,因此dp[i][j][k]等价于dp[i][k][j],因此,在循环的时候可以令j<=k;然后加几个判断即可。具体方法不再赘述,请自行解决。
2.空间复杂度的优化:
在求解的过程中 即:dp[i][j][k]的值 只与 dp[i-1][…][…]的值有关,因此可以将数组降为2维 即:dp[j][k],具体方法不再赘述。可以看标程,标程有两个,一个是优化过的,一个是未经过优化的。
因此,对于这道题目,
近似最优时间复杂度为O(n^3)
近似最优空间复杂度为O(n^2)

1 #include<stdio.h> 2 int dp[501][501]={0}; 3 int t1[101]={0},t2[101]={0},w[101]={0},t,n; 4 5 void quick_sort(int l,int r)//按t2升序排序 6 {int i,k,a; 7 if(l>=r) 8 return; 9 k=l-1; 10 for(i=l;i<r;i++) 11 if(t2[i]<t2[r]) 12 {k++; 13 a=t2[k]; 14 t2[k]=t2[i]; 15 t2[i]=a; 16 a=t1[k]; 17 t1[k]=t1[i]; 18 t1[i]=a; 19 a=w[k]; 20 w[k]=w[i]; 21 w[i]=a; 22 } 23 a=t2[k+1]; 24 t2[k+1]=t2[r]; 25 t2[r]=a; 26 a=t1[k+1]; 27 t1[k+1]=t1[r]; 28 t1[r]=a; 29 a=w[k+1]; 30 w[k+1]=w[r]; 31 w[r]=a; 32 quick_sort(l,k); 33 quick_sort(k+2,r); 34 } 35 36 FILE *fin,*fout; 37 main() 38 {fin=fopen("medic.in","r"); 39 fout=fopen("std.out","w"); 40 int i,j,k,q,a; 41 fscanf(fin,"%d%d",&t,&n); 42 for(i=1;i<=n;i++) 43 fscanf(fin,"%d%d%d",&t1[i],&t2[i],&w[i]); 44 quick_sort(1,n); 45 for(i=1;i<=n;i++)//动态规划 46 for(j=t;j>=0;j--) 47 for(k=t;k>=0;k--) 48 {if(j>=t2[i]) 49 if(dp[j][k]<dp[t1[i]-1][k]+w[i]) 50 dp[j][k]=dp[t1[i]-1][k]+w[i]; 51 if(k>=t2[i]) 52 if(dp[j][k]<dp[j][t1[i]-1]+w[i]) 53 dp[j][k]=dp[j][t1[i]-1]+w[i]; 54 } 55 fprintf(fout,"%d",dp[t][t]); 56 fclose(fin); 57 fclose(fout); 58 }
二、我写的费用流我看到这道题,嘴上笑嘻嘻,心里mmp,看起来又是一道DP/贪心题?
我最讨厌的就是这个东西了
于是联想以前的题目想到了USACO Nov07挤奶时间 那到题,是个单线程的求最大收益值,于是我就u->v连了条权值为收益的边,跑遍最长路
这道题不就是把单线程改成了双线程吗?两次最长路是显然错误的,因为不一定是最优。但他在跑完之后能反悔就好了
反悔?我们想到了网络流的反向边,于是我们尝试把这道题转化成一个网络流的模型
u->v+1连一条费用为收益,流量为1的边(v+1是因为包括了末节点的时间),然后从起点到终点,连一条i->i+1,费用为0,流量为2的边
这样限制了进程数为2,同时跑一边最大费用最大流,就AC了 (然后这样的算法完爆STD?测试我的0s ,std 0.7s)

1 #include<set> 2 #include<map> 3 #include<stack> 4 #include<queue> 5 #include<cstdio> 6 #include<cstring> 7 #include<iostream> 8 #include<algorithm> 9 #define RG register int 10 #define rep(i,a,b) for(RG i=a;i<=b;i++) 11 #define per(i,a,b) for(RG i=a;i>=b;i--) 12 #define ll long long 13 #define inf (1<<30) 14 #define maxm 5005 15 using namespace std; 16 int n,m,S,T,cnt=1; 17 int head[maxm],dis[maxm],step[maxm],vis[maxm]; 18 struct E{ 19 int u,v,fl,cost,next; 20 }e[maxm]; 21 inline int read() 22 { 23 int x=0,f=1;char c=getchar(); 24 while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();} 25 while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();} 26 return x*f; 27 } 28 29 inline void add(int u,int v,int fl,int cost) 30 { 31 e[++cnt].u=u,e[cnt].v=v,e[cnt].fl=fl,e[cnt].cost=cost,e[cnt].next=head[u],head[u]=cnt;swap(u,v); 32 e[++cnt].u=u,e[cnt].v=v,e[cnt].fl=0,e[cnt].cost=-cost,e[cnt].next=head[u],head[u]=cnt; 33 } 34 35 bool SPFA() 36 { 37 memset(dis,63,sizeof(dis)); 38 memset(step,-1,sizeof(step)); 39 memset(vis,0,sizeof(vis)); 40 queue<int> que;que.push(S),dis[S]=0;RG u,v; 41 while(!que.empty()) 42 { 43 u=que.front(),que.pop();vis[u]=0; 44 for(RG i=head[u];i;i=e[i].next) 45 { 46 v=e[i].v; 47 if(e[i].fl&&dis[v]>dis[u]+e[i].cost) 48 { 49 dis[v]=dis[u]+e[i].cost; 50 step[v]=i; 51 if(!vis[v]) vis[v]=1,que.push(v); 52 } 53 } 54 } 55 return (step[T]!=-1); 56 } 57 58 void MCMF() 59 { 60 int ans=0; 61 while(SPFA()) 62 { 63 int fl=inf; 64 for(RG i=step[T];i!=-1;i=step[e[i].u]) fl=min(fl,e[i].fl); 65 for(RG i=step[T];i!=-1;i=step[e[i].u]) e[i].fl-=fl,e[i^1].fl+=fl,cout<<e[i].v<<" "; 66 ans+=dis[T]; 67 } 68 cout<<-ans; 69 } 70 71 int main() 72 { 73 freopen("medic.in","r",stdin); 74 freopen("medic.out","w",stdout); 75 n=read(),m=read();S=0,T=n+1; 76 for(RG i=1,u,v,cost;i<=m;i++) u=read(),v=read(),cost=read(),add(u,v+1,1,-cost); 77 rep(i,2,n) add(i-1,i,2,0); 78 add(S,1,2,0);add(n,T,2,0); 79 MCMF(); 80 return 0; 81 }
标签:image 除了 优化 文件 最大费用最大流 加工 .com stream char
原文地址:http://www.cnblogs.com/ibilllee/p/7716864.html