斯坦福2014机器学习笔记六----神经网络（一）

标签：描述   技术   嵌套   简化   src   输入   逻辑回归   矩阵   表达   

 一、纲要

　　神经网络模型表示

　　神经网络的直观理解

　　神经网络做多类分类

二、内容详述

　　1、神经网络模型表示

　　这里就不再描述大脑的神经网络和神经元了，我们直接看神经网络的模型。我们先从最简单的神经网络开始，即只有input layer和output layer

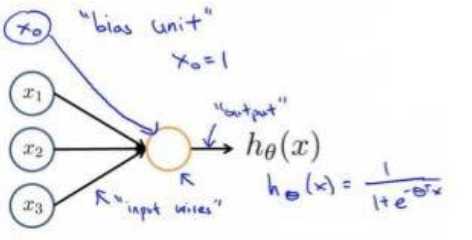
这里的x₀叫做偏置单元，跟之前一样，为一常数，x₀=1；这里的h_θ(x)叫做神经元的激励函数，h_θ(x)跟逻辑回归函数一样。下面再来一个相对来说复杂一点的神经网络

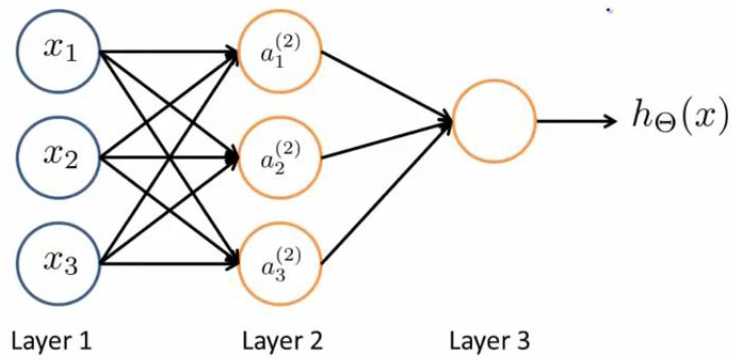
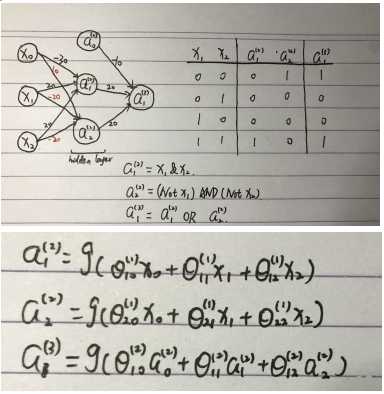
这里多了一层layer2，叫做隐藏层(hidden layer)。我们用a_i^(j)表示第j层的第i个激励，用θ⁽ⁱ⁾表示第j层到第(j+1)层的作用，且θ⁽ⁱ⁾是一个矩阵，尺寸是(j+1)层的单元数S_j+1为矩阵的行数，第j层的单元数S_j+1表示为矩阵的列数，即θ的维度是(S_j+1 * S_j+1)。这样的话我们就可以算出layer2的各单元的表达式：

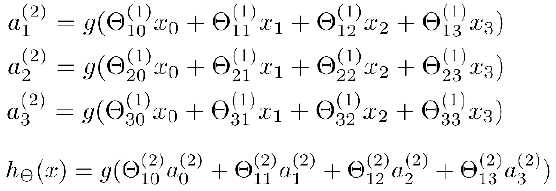
这里在计算layer2的时候会加上x₀，如果有更多的层，在计算下一层的时候都会加上这层的偏置单元，如在计算layer3的时候就在layer2画上a₀⁽²⁾这个bias unit。

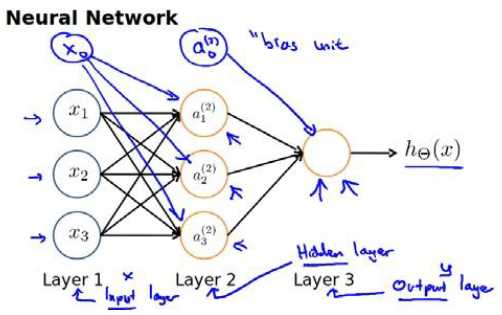
这里我们可以对上面的表达式进行简化表示如图，并对z，x，θ进行向量化得z⁽ⁱ⁺¹⁾ = θ⁽ⁱ⁾·x⁽ⁱ⁾，i表示对应第i层

可以看得出，每一层的a都是由上一层的x和x对应的参数(权重)θ决定的，我们把这样从左到右的算法称为前向传播算法。

说了这么多，神经网络所做的就是逻辑回归，但输入不再是x₁ x₂ x₃，而是用a₁ a₂ a₃的计算出来的新输入特征，这里的a₁ a₂ a₃都是逻辑回归的结果，因为是梯度下降的，所以我们得到的a₁ a₂ a₃是比x₁ x₂ x₃更好的假设，然后再输入到最后一层，相当于是逻辑回归的多层嵌套。

　　2、神经网络的直观描述

　　这一部分我们来利用神经网络实现逻辑与、逻辑或，逻辑非运算，然后用稍微复杂的神经网络来实现同或运算

我们假设这里的权重θ₀ = -30，θ₁ = 20，θ₂ = 20，那么进行运算后我们得到，根据我们之前逻辑回归部分的h_θ(x)=g(z)，当z>4.6时我们可以认为h_θ(x)=g(z) = 1，而当z<-4.6时，认为h_θ(x)=g(z)=0，所以我们对x₀，x₁分别赋0、1值可以得到真值表。这就是神经网络实现了AND运算

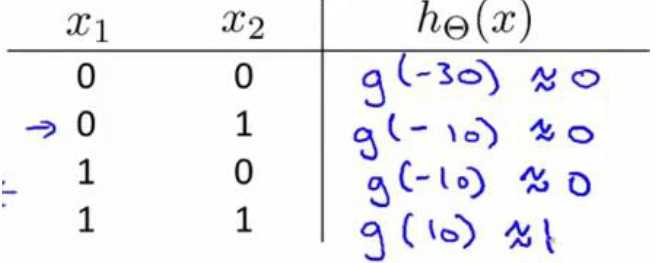
　　我们用同样的方法进行(Not x₁)AND(Not x₂)运算，此时权重就应该变为θ₀ =10，θ₁ = -20，θ₂ = -20，可以自己动手画一画。这些都是只有input layer和output layer，下面我们要实现同或运算，就需要额外的hidden layer，这里我直接手写来表示

　　3、神经网络做多类分类

　　多类分类就是说在output layer有多个输出，跟上面这部分的区别在于，上面的都是二元分类，只有一个输出，即非1即0。但是做多类分类的时候，加入我们需要识别4类不同的对象，那我们就需要4个输出，且我们得到的输出值h_θ(x)=y⁽ⁱ⁾=[1,0,0,0]^(T)或[0,1,0,0]^(T)或[0,0,1,0]^(T)或[0,0,0,1]^(T)，这样我们就可以判断识别的是哪类对象了

斯坦福2014机器学习笔记六----神经网络（一）

标签：描述   技术   嵌套   简化   src   输入   逻辑回归   矩阵   表达   

原文地址：http://www.cnblogs.com/kl2blog/p/7719981.html