贝叶斯概率综述和课堂思路整理.2

标签：积分   决策   src   求导   5.5   包含   分享   问题   ges   

这次来讲讲尼曼皮尔森决策（Neyman-Pearson），两类错误率和ROC曲线

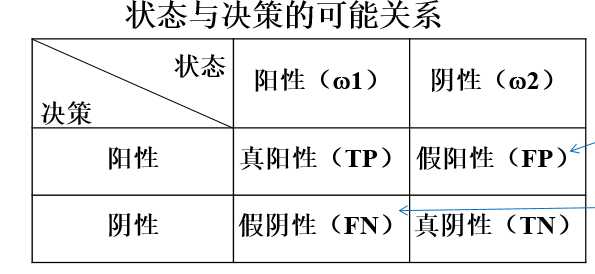
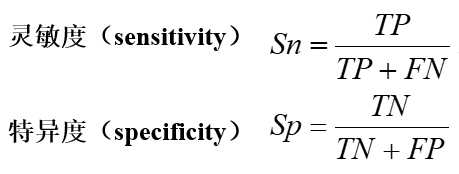
在一些情况下，要求将一类的错误率控制在一个常数，满足此前提的情况下要求另一个错误率尽可能小，而与总的错误代价无关

这便是Neyman-pearson决策

关于求解过程，一般使用Lagrange乘子法

转化为另一类问题：

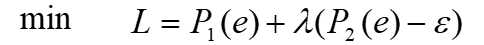
设边界为R，分出决策域R1，R2

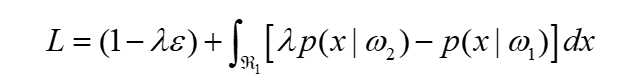
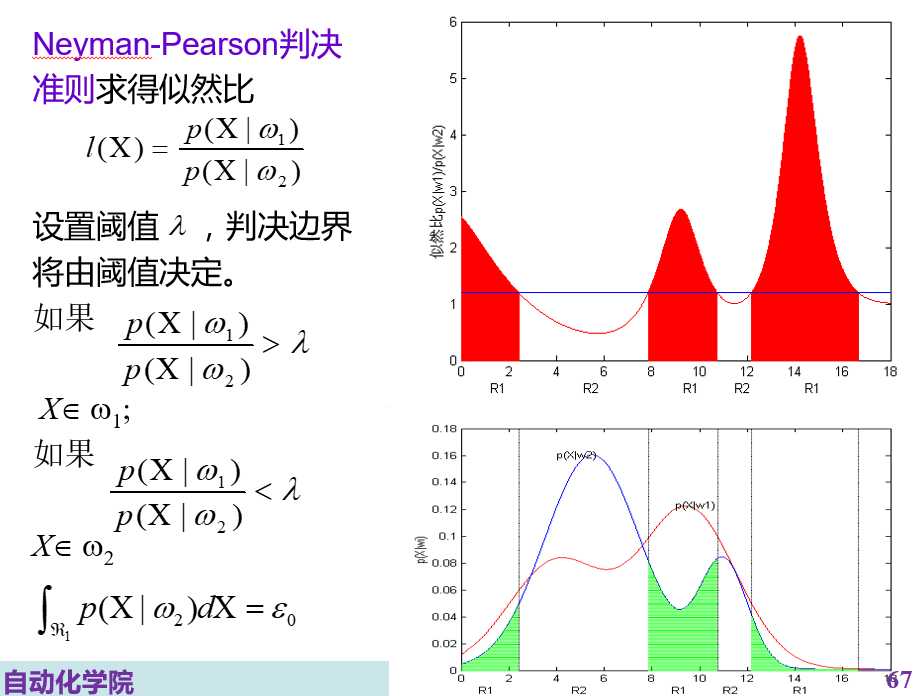
P₂(e)=∫_R1 P(x|w₂) dx,P₁(e)=∫_R2 P(|w₁) dx=1-∫_R1 P(x|w1) dx

在二位特征域中计算过于复杂且不实用，在此只讨论一维情况

则设决策点为t

求L最小值，对L求导为0

需要注意的是，确定的错误率不代表有确定的边界，因为决策点不止有一个，决策域也不一定是连续的（在一维情形下不是简单的决策点左边分为A，右边分为B，而是某些个区域分为A，某些个区域分为B）

另一种比较直观的解释是：由于求最小，所以积分域一定包含了所有的负值区域，即所有的l(x)>λ的时候，是将该区域划分为w1，以算P1(e)的计算中去

保证划分的区域P2(e)=ε,同时划分区域的边界

判决边界t将由λ决定，则决策区域也将由λ决定，P2(e)也将由λ决定，可以证明以λ为自变量的P2(e)是单调函数（λ越大，区域越少，P2(e)越小）

于是对于固定的P2(e)有着固定的λ

先写到这，ROC曲线定义比较简单暂时略过

贝叶斯概率综述和课堂思路整理.2

标签：积分   决策   src   求导   5.5   包含   分享   问题   ges   

原文地址：http://www.cnblogs.com/Levius/p/7722901.html