【线性筛】

标签：理解   strong   color   lin   image   整数   奇数   代码   范围   

在这里提供三种线性筛的讲解,它们分别是:素数筛,欧拉筛和莫比乌斯筛。

·筛法正确性的重要理论依据：

上述函数均为积性函数。积性函数的性质为:若f(x)是一个积性函数,那么对于任意素数a,b,满足f(ab)=f(a)*f(b)

·一些可爱的要点(有助于理解筛法原理)：

①欧拉筛和莫比乌斯筛是以素数筛为基础的。

②三者在代码实现上几乎是同一框架。

③欧拉函数和莫比乌斯函数的定义介绍：

     (1)欧拉函数Phi(x)表示小于等于x的正整数中和x互质的数的个数(注意,1与任何数互质)。

     (2)莫比乌斯函数Mob(x)仅有三种值:0,-1,1————如果x能够被一个大于0的整数的平方整除，那么函数值为0;如果x拥有奇数种 质因数，那么函数值为-1，有偶数种质因数，那么函数值为1(莫比乌斯函数的神奇定义决定了它应用于容斥问题......)。

·线筛步骤：

(1)获得范围内的素数

      线性筛的线性体现在尽可能的使每个数只被“筛”一次。其思想众所周知地基于： a为任何数,b为质数,那么a*b就不是质数。

     在程序实现中体现为，对于当前枚举的数i,使用所有小于等于i的素数p，去“筛除”数(p * i),即将布尔数组对应位置设为1(表示不为素数)。

      值得注意的是，这里会出现三个筛法都会 涉及的关键语句：“if(i%Prime[j]==0)break;”。这是一个很简单有效的优化，原理依旧是基于“尽量只筛一次”。

     下面对这个优化做出解释:在这里我们提出“最小质因子”的概念，然后我们规定每个合数都只被它的最小质因子筛出————这个定义很好地契合了“尽可能只筛一次”的想法。

     回到问题，当前如果出现"i%Prime[j]==0"的情况，由于枚举素数Prime[j]是从小到大的,那么可以说明Prime[j]是i的最小质因子。

     此时如果不终止循环，那么Prime[j+1],Prime[j+2]...会与i相乘得到结果然后筛掉这个结果，但是我们从式子中看出，得到的结果的最小质因子是Prime[j],然而我们使用了j之后的素数筛掉了它，不符合开始的原则，这样做 会使得一个数被筛多次，降低了效率。举例说明则是：20应该由2 * 10筛掉，而不是被4 * 5筛掉(素数2<素数5)。

然后这里就给出素数筛代码吧吧吧：

(2)正式开筛

(一)欧拉函数的线性筛

首先给出欧拉函数的定义式子：(p表示x的质因数)

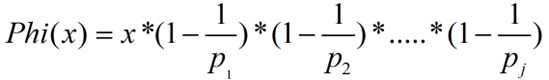
然后考虑如何用类似于筛素数的方法筛出欧拉函数。

类似于素数,可以做出如下分类讨论：(设p为素数)
     ①Phi(p)=p-1

     ②若已知Phi(x),且p能整除x: Phi(x*p)=Phi(x)*p

     ③若已知Phi(x),且p不能整除x：Phi(x*p)=Phi(x)*(p-1)

简单地证明上述式子：对于①,由于p本身是一个素数，那么比它小的所有数都和它互质，因此答案为p-1。对于②,p已经是x的质因子,因此我们看看欧拉函数的定义式可以的出括号相乘部分不会改变,只会把最前面的x变成x*p。对于③,p是新加入的质因子,相当于式子前面多乘了个p,然后多加了一个括号，所以相当于原式多乘了: p*(1-1/p)即(p-1)。

    呆码在这里：
 

(二)莫比乌斯函数的线性筛

【线性筛】

标签：理解   strong   color   lin   image   整数   奇数   代码   范围   

原文地址：http://www.cnblogs.com/Paul-Guderian/p/7723031.html