标签:print mes -- ret end alt 复杂度 stream 通过
题目传送门:https://www.luogu.org/problemnew/show/P2822 ↓题目大意↓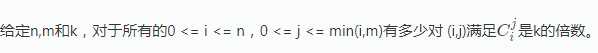
数据的极限范围:n,m≤2000,k≤21,数据组数≤10000。
由于此题k不大于21,故在计算组合数Cij时,并不需要存储它的真实数值,只需要存储其≤19的所有素因子的个数,判断Cij是否为k的倍数,仅需要判断Cij中各素因子的个数是否大于等于k中的个数即可。基于组合数的性质,我们如果要求出Cij,我们可以通过Ci(j-1)乘上i-j+1然后再除以j即可得到。
下面来考虑如何乘以或除以一个数x。若需要在Ci(j-1)的基础上乘以x,可以考虑将x分解质因数,仅将其≤19的全部素因子与Ci(j-1)的素因子个数进行累加。除法同理,加法改成减法即可。
最后维护一个二维数组b。若b[i][j]=1,则表示Cij是k的倍数。输入n,m时,将b[1..n][1..m]进行累加即可得出答案。很明显这么操作依然会TLE,使用另一数组维护b[i][j]的前缀和即可。
时间复杂度为O(n*m+T)。 但常数很大(本地均为0.3s左右)。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #define M 2000 5 using namespace std; 6 int p[]={2,3,5,7,11,13,17,19}; 7 struct cg{ 8 int a[8]; 9 cg(){memset(a,0,sizeof(a));} 10 cg(int x){ 11 for(int i=0;i<8;i++) 12 while(x%p[i]==0) a[i]++,x/=p[i]; 13 } 14 friend cg operator *(cg a,int x){ 15 for(int i=0;i<8;i++) 16 while(x%p[i]==0) a.a[i]++,x/=p[i]; 17 return a; 18 } 19 friend cg operator /(cg a,int x){ 20 for(int i=0;i<8;i++) 21 while(x%p[i]==0) a.a[i]--,x/=p[i]; 22 return a; 23 } 24 friend bool operator +(cg a,int x){ 25 cg c=a; 26 for(int i=0;i<8;i++) 27 while(x%p[i]==0){ 28 c.a[i]--;x/=p[i]; 29 if(c.a[i]<0) return 0; 30 } 31 return 1; 32 } 33 }a[M+10][M+10]; 34 int b[M+10][M+10]={0},k; 35 36 void init(){ 37 for(int i=1;i<=M;i++){ 38 int zhi=i>>1; 39 for(int j=1;j<=zhi;j++) 40 a[i][j]=a[i][i-j]=a[i][j-1]*(i-j+1)/j; 41 } 42 for(int i=1;i<=M;i++){ 43 int zhi=i>>1; 44 for(int j=1;j<=zhi;j++){ 45 b[i][j]=b[i][i-j]=a[i][j]+k; 46 } 47 } 48 for(int i=1;i<=M;i++) 49 for(int j=1;j<=M;j++){ 50 b[i][j]=b[i-1][j]+b[i][j-1]-b[i-1][j-1]+b[i][j]; 51 } 52 } 53 54 int main(){ 55 freopen("problem.in","r",stdin); 56 freopen("problem.out","w",stdout); 57 int cas; cin>>cas>>k; 58 init(); 59 while(cas--){ 60 int x,y; scanf("%d%d",&x,&y); 61 printf("%d\n",b[x][y]); 62 } 63 }
标签:print mes -- ret end alt 复杂度 stream 通过
原文地址:http://www.cnblogs.com/xiefengze1/p/7725115.html