标签：习惯 无法 理解 type 意义 表示 用例 系统 是什么
根据定义，这个序列作为函数的系数，称G(x)就是序列的母函数。和一般意义上的函数相比，母函数的功能是计数。
从百度和维基上能找到的相关说明都显得太学院派，不容易理解，还是用例子说明并引入吧。
有这样一道例题：
到这一章为止，已知的计数法则就两种，加法法则（或）和乘法法则（且）。前者是分类思想，后者是分步。
法1:分步来看，第一个骰子有1-5种可能，因为两个骰子之和是6，所以一旦第一个骰子确定了，第二个骰子也就随之确定。第一个骰子的每一种可能性都仅对应第二个骰子的唯一确定的点数。因此5*1=5种。
法2:分类来看，有可能是1+5=5+1或2+4=4+2或3+3=3+3，累加起来，一共五种可能。
当然这个是最最简单的例子，也很容易想，但如果骰子有很多呢？
这种情况下，挨个挨个地枚举显然是愚蠢的。而伯努利在300年前已经研究过这个问题了，是关于“投掷m粒骰子时，点数总和为n的可能方案数”，这个问题乍看之下很复杂，令人怀疑人生。
那么先从简单情形考虑，两个骰子掷出n点，有多少种可能。这相当于把n拆分成两个数的和，这时候对n枚举就很复杂，所以对两个骰子枚举。第一个骰子，6种可能，相互之间是“或”的关系，对应的是加法，但是不能直接相加，因为这无法反映两个骰子的叠加过程。
我们需要逐个分析一个骰子的不同情况，对于一个骰子，假如掷出2个点，就可以看作一个分步策略，相当于——先掷一个点，再掷一个点，所以是(●)^2，当然这样不习惯，于是用x^2来表示。那四个点是x^4,因此可以用指数对应点数。
这样就可以用（x+x^2+…+x^6）表示一个骰子的投掷过程，对于第二个骰子也是这样，最后两式相乘，x^6前面的系数就是有多少种出现6点的方案。
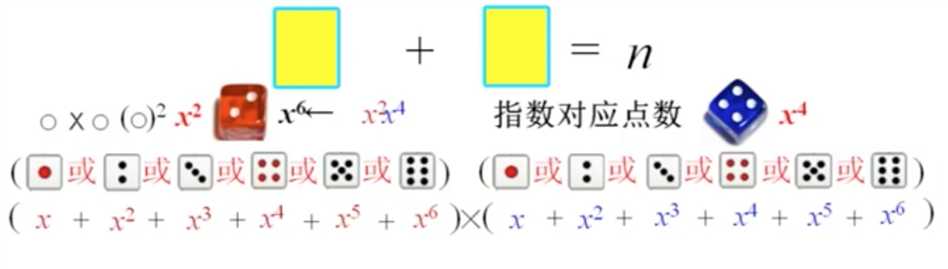
最后的母函数求出来是
两个骰子掷出n点的可能方法数就是求G(x)中x^n的系数。实际上系数起了关键性的作用，母函数中的系数对应了计数序列。
那么回溯到最初伯努利提出的问题，m粒骰子就是m个多项式累乘
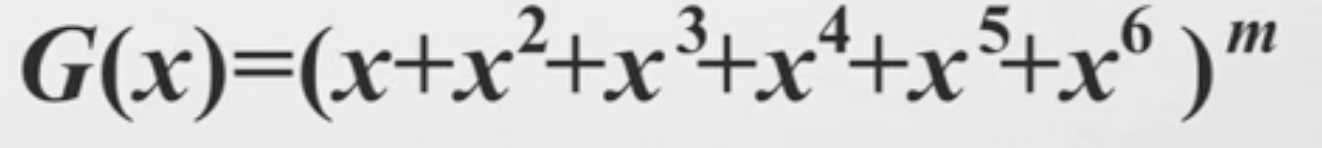
而要求点数总和为n的可能方案数，也就是求展开式中x^n的系数。这可以看出来，对于这个多项式，我们并不关心它的值，现在关心的却是它的系数了。（所以母函数确实是一位母亲，计数序列作为系数就是她的孩子233）
所以母函数的定义我们可以进一步提炼出两点
而这个定义是拉普拉斯在研究概率的时候，研究了母函数的方法和相关定义。（1812年拉普拉斯在著作《概率的分析理论》第一卷中系统地研究了母函数的方法和有关理论）
最后总结一下，母函数实际上是用来做什么的，以及它和函数有什么区别。
对于母函数
虽然形式上是函数，但“似函数，非函数”。
那——为什么要引入一个母函数呢？因为在现实世界里，对于各种复杂的事件，我们要通过“映射”的方式将其简化，比如说对于分数幂的运算十分困难，我们用一个对数映射将其简化，再求原问题的解，就相对容易了。
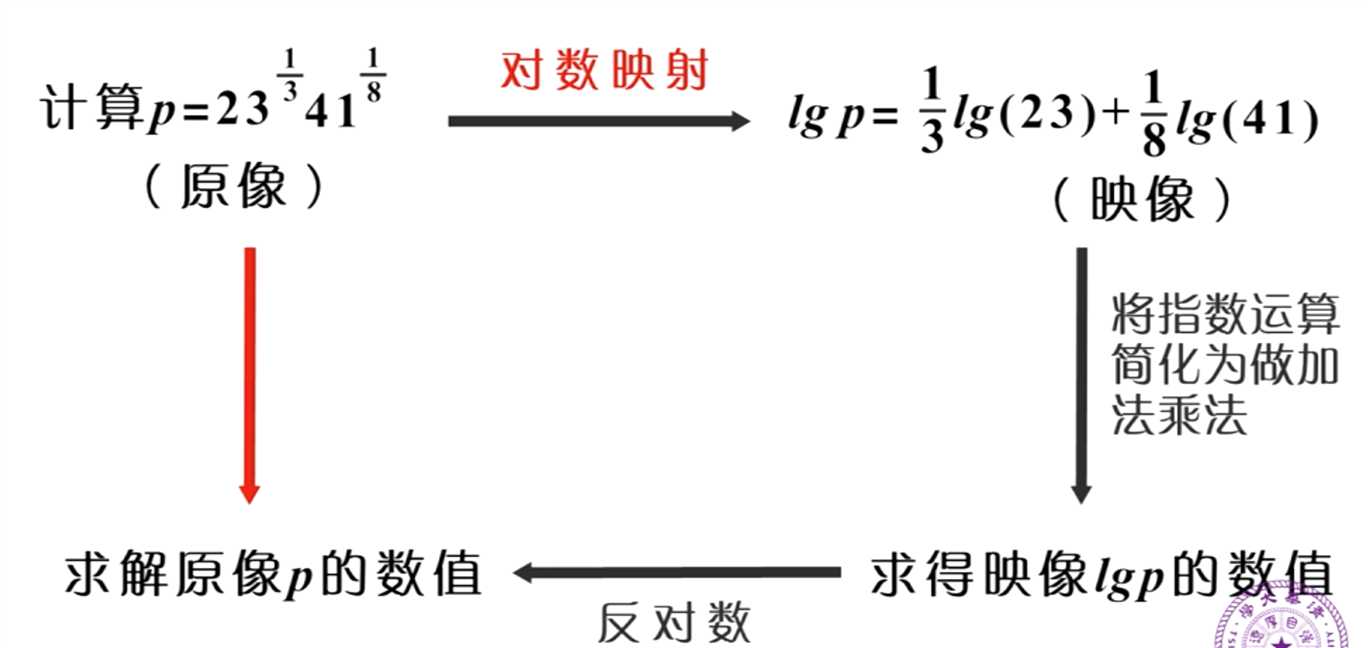
在母函数中同样如此，在一开始思考的骰子问题里，直接计算是十分困难的，后来发现通过分步来考虑的时候，把多项式引入，求出相应系数后再对应回来，就得到了解。
其实母函数蕴含的就是一种映射关系。
那么是什么原因使得母函数具备了计数的法则呢，在骰子那道题中，通过求系数来对应方案数是一个例子。分析一下，对于一般的多项式，可以写成
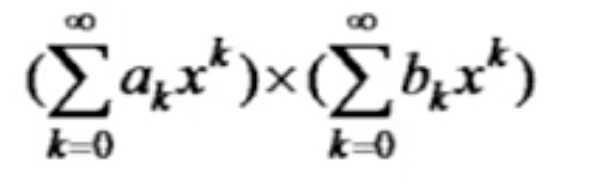
这种形式，展开后的某个幂次的系数可以分为两部分，分别来自于两个括号里的某一项，这实际上就是对应的乘法法则
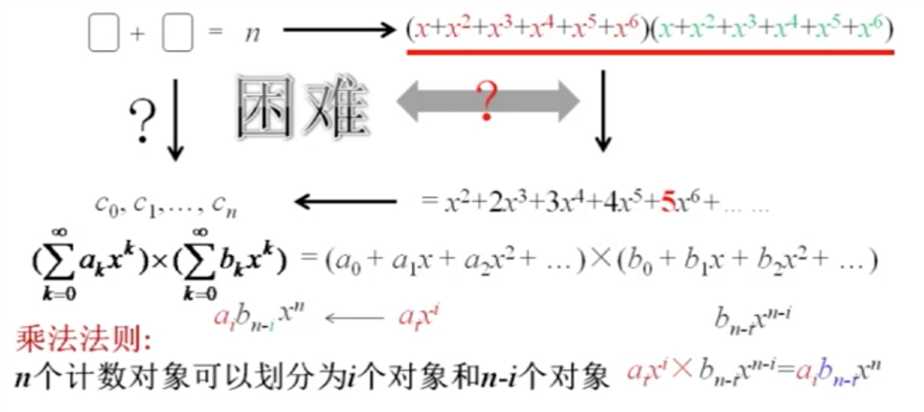
所以实质上是多项式的乘法运算使母函数具有了计数能力。
“母函数就是一列用来展示一串数字序列的挂衣架”
——赫伯特·维尔夫
标签：习惯 无法 理解 type 意义 表示 用例 系统 是什么
原文地址：http://www.cnblogs.com/hongshijie/p/7727000.html
