羊车门问题

标签：bsp   主持人   inpu   http   print   编写   结果   随机数函数   两种   

有3扇关闭的门，一扇门后面停着汽车，其余门后是山羊，只有主持人知道每扇门后面是什么。参赛者可以选择一扇门，在开启它之前，主持人会开启另外一扇门，露出门后的山羊，然后允许参赛者更换自己的选择。

请问：

1、按照你的第一感觉回答，你觉得不换选择能有更高的几率获得汽车，还是换选择能有更高的几率获得汽车？或几率没有发生变化？

答：      我认为换选择能有更高的几率获得汽车

2、请自己认真分析一下“不换选择能有更高的几率获得汽车，还是换选择能有更高的几率获得汽车？或几率没有发生变化？” 写出你分析的思路和结果。

答：       我们可以考虑到总共有两种情况：

              1、参赛者不更换选择，他获得汽车的概率就是1/3；

              2、参赛者更换选择：假如说羊所在的门标记为x和y，车所在的门标记为a。那么参赛者可以有这几种选择：

                              1、参赛者第一次选择了x,那么他改变选择就一定可以选中车（a）

                              2、参赛者第一次选择了y,那么他改变选择就一定可以选中车（a）

                              3、参赛者第一次选择了a,那么他改变选择就一定不会选中车（a）

                        所以，参赛者选中车的概率为2/3

3、请设法编写程序验证自己的想法，验证的结果支持了你的分析结果，还是没有支持你的分析结果，请写出结果。（提示：可以借助随机数函数完成此程序）

答：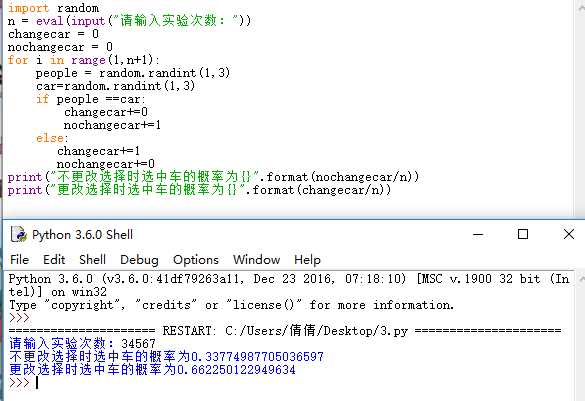

支持了分析结果

4、请附上你的代码。（提示：使用编辑器中的插入代码功能，将代码显示为 Python 风格）

代码如下：

 1 import random
 2 n = eval(input("请输入实验次数："))
 3 changecar = 0
 4 nochangecar = 0
 5 for i in range(1,n+1):
 6     people = random.randint(1,3)
 7     car=random.randint(1,3)
 8     if people ==car:
 9         changecar+=0
10         nochangecar+=1
11     else:
12        changecar+=1
13        nochangecar+=0
14 print("不更改选择时选中车的概率为{}".format(nochangecar/n))
15 print("更改选择时选中车的概率为{}".format(changecar/n))

羊车门问题

标签：bsp   主持人   inpu   http   print   编写   结果   随机数函数   两种   

原文地址：http://www.cnblogs.com/mnln/p/7685013.html