标签：注释 poi tool ati 自然界 消元 3.2 双线性插值 取消
一.三角化得到空间点的三维信息(深度值)
(1)三角化的提出
三角化最早由高斯提出，并应用于测量学中。简单来讲就是：在不同的位置观测同一个三维点P(x, y, z)，已知在不同位置处观察到的三维点的二维投影点X1(x1, y1), X2(x2, y2)，利用三角关系，恢复出三维点的深度信息z。
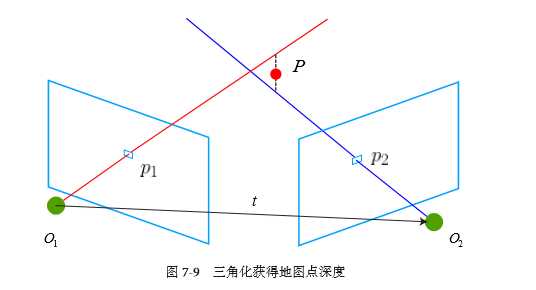
(2)三角化公式
按照对极几何中的定义，设x1, x2为两个特征点的归一化坐标，则它们满足：
s1x1 = s2Rx2 + t 公式(1)
=> s1x1 - s2Rx2 = t 公式(2)
对公式(2)左右两侧分别乘以x1T，得：
s1x1Tx1 - s2x1TRx2 = x1T t 公式(3)
对公式(2)左右两侧分别乘以(Rx2)T，得：
s1(Rx2)Tx1 - s2(Rx2)TRx2 = (Rx2)T t 公式(4)
由公式(3)和公式(4)可以联立得到一个一元二次线性方程组，然后可以利用Cramer‘s法则（参见线性代数书）进行求解。
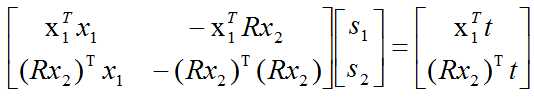
如下是对应的代码（如果大家感觉不易读懂，可以先跳过这段代码，等看完理论部分再返回来看不迟）
1 // 方程 2 // d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC 3 // => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t] 4 // [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t] 5 // 二阶方程用克莱默法则求解并解之 6 Vector3d t = T_R_C.translation(); 7 Vector3d f2 = T_R_C.rotation_matrix() * f_curr; 8 Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) ); 9 double A[4]; 10 A[0] = f_ref.dot ( f_ref ); 11 A[2] = f_ref.dot ( f2 ); 12 A[1] = -A[2]; 13 A[3] = - f2.dot ( f2 ); 14 double d = A[0]*A[3]-A[1]*A[2]; 15 Vector2d lambdavec = 16 Vector2d ( A[3] * b ( 0,0 ) - A[1] * b ( 1,0 ), 17 -A[2] * b ( 0,0 ) + A[0] * b ( 1,0 )) /d; 18 Vector3d xm = lambdavec ( 0,0 ) * f_ref; 19 Vector3d xn = t + lambdavec ( 1,0 ) * f2; 20 Vector3d d_esti = ( xm+xn ) / 2.0; // 三角化算得的深度向量 21 double depth_estimation = d_esti.norm(); // 深度值
(3)求解深度的另外两种方法
a.利用叉乘进行消元进行求解
由
s1x1 = s2Rx2 + t 公式(1)
左右两边同时乘以x1的反对称矩阵，可得：
s1x1^x1 = 0 = s2x1^Rx2 + x1^t 公式(2)
由上式可解得s2，将s2代入公式(1)，可求得s1
b.利用Mid Point Method进行求解(Hartley大名鼎鼎的《Multiple View Geometry》中有讲解)
从此图中我们可以知道，理想情况下O1P和O2P会相交于空间中的一点，但是由于图像分辨率以及噪声的存在，实际的情况更可能是上图所描述的那样：O1P和O2P在空间中没有交点，这时我们需要找到一个O1P与O2P之间的公垂线，然后取其上的中点作为我们重建出的三维点，此即为Mid Point Method，具体的推导及公式请参看Hartley的《Multiple View Geometry》。【需要将上面的图想象的立体一些】
附：
1.Cramer‘s 法则：
如果A的行列式不为0， Ax=b可以通过如下行列式进行求解：
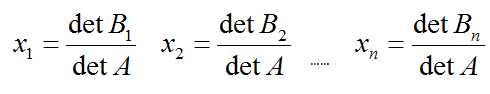
矩阵Bj为A的第j列被b替换后得到的新的矩阵。
二.三角化得到的三维信息中深度的误差
(1)三角化中误差分析
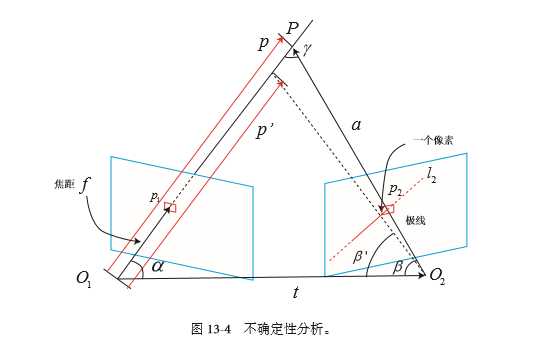
如上图所示：
P为空间中的一个三维点，p1和p2分别为在两个位置处，摄像机观察到的投影的二维点坐标。
l2为p1在第二幅图中所对应的极线（极线的概念请参考立体视觉中的对极几何，这里不再赘述）。
现在，我们要探讨的是：
如果我们在l2进行极线搜索时，所找到的p2‘点与真实的p2点有一个像素的误差，那么会给三角化后的三维点P的深度z带来多大的误差？
首先，根据上图，我们可以得到向量之间的关系，以及三角化中的两个夹角的定义：
a = p - t 公式(1)
α = arccos<p, t> 公式(2)
β = arccos<a, -t> 公式(3)
其中，a, p, t均为向量，α和β为图中所示的两个夹角。
如果此时，我们求取的p2‘点与p2点有一个像素的偏差，同时，这一个像素的偏差又会给β带来δβ的角度变化，我们利用β‘来表示对β进行δβ扰动后的新的角度。
设相机的焦距为f，则：
公式(4):
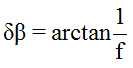
公式(5):
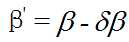
公式(6):
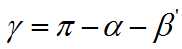
至此，加入扰动后的所有新的角度我们都求出来了。
由正弦定理（a/sinA=b/sinB=c/sinC），我们可以得到：
公式(7):
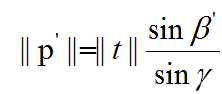
则由第二个位置上的二维点的一个像素的误差，可能导致的三角化后深度的误差为：
δp = ||p|| - ||p‘||
这里的δp其实也正是深度的一个均方差（不确定度σobs），这个不确定度是我们后面要介绍的深度滤波器的一个很重要的概念，深度滤波器的目的也正是要不断减小这个不确定度，使得深度的不确定度最后能够收敛到一个能够接受的值。
(2)三角化中误差的来源
上面分析了第二幅图中的特征点p2的误差是如何影响三角化后的深度值的。
下面，我们来指出三角化的误差来源有哪几方面：
a.图像的分辨率：图像的分辨率越高，一个像素所带来的δβ就越小。
b.特征点求取时的精度：是否做到亚像素，在亚像素的基础上，误差有多大？
c.p1点的误差：会引起极线l2的误差，从而间接地影响p2点的精度。
d.相机两次位置的平移向量t的大小：t的模的大小也代表了对极几何中的基线长度，由公式(7)可以看出基线长度越大，三角化的误差越小。
所以，这也体现出来了三角化的矛盾：若想提高三角化的精度，其一提高特征点的提取精度，即提高图像的分辨率，但这会导致图像的增大，增加计算成本；其二，使平移量增大，但这会导致图像外观的明显变化，外观变化会使得特征提取与匹配变得困难。总而言之，平移太大，会导致匹配失效；平移太小，三角化精度不够。
(3)如何减小三角化所带来的误差
根据【(2)三角化中误差的来源分析】中所分析的一些因素可知，要想减小三角化过程中引入的误差，可以有如下几个方法：
a.选取尽可能高分辨率的相机。
b.进行亚像素的优化（比如在极线搜索时对像素点坐标进行双线性插值）
// 双线性灰度插值
inline double getBilinearInterpolatedValue( const Mat& img, const Vector2d& pt )
{
uchar* d = & img.data[ int(pt(1,0))*img.step+int(pt(0,0)) ];
double xx = pt(0,0) - floor(pt(0,0));
double yy = pt(1,0) - floor(pt(1,0));
return (( 1-xx ) * ( 1-yy ) * double(d[0]) +
xx* ( 1-yy ) * double(d[1]) +
( 1-xx ) *yy* double(d[img.step]) +
xx*yy*double(d[img.step+1]))/255.0;
}
（关于双线性插值，这篇文章做了比较清晰的讲解：http://blog.163.com/guohuanhuan_cool@126/blog/static/167614238201161525538402/）
c.同样使用亚像素级的图像处理算法来处理p1点。
d.在不丢失特征点的情况下，让平移量t尽量大。
由上面的公式推导我们可以看出，三角化中，必须要有平移量t，否则无法构成三角形，进行三角化。所以在有些单目的SLAM，AR/VR的场景中，有经验的人都会有意识地将设备或者相机进行一定量的平移，而不会在原地进行纯旋转。
三.深度滤波器的原理及实现
介绍的是比较简单的高斯分布假设下的深度滤波器。
高斯分布是自然界中最常见的一种分布形式，并且也符合绝大部分的自然情况。简单起见，我们先假设三角化后恢复的深度值符合高斯分布。
对于像素点的深度值d，满足：P(d) = N(μ，σ2)
每当新的数据过来，我们就要利用新的观测数据更新原有的深度d的分布。
这里的数据融合的方式与经典的Kalman滤波方式大同小异。这里，我们利用观测方程进行信息融合。
假设新计算出来的深度数据的分布为：P(dobs) = N(μobs，σobs2)
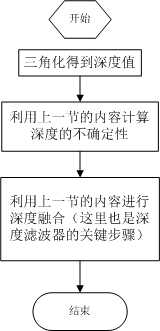
我们将新计算出来的深度数据乘在原来的分布上，进行信息融合，得到融合后的高斯分布：P(dfuse) = N(μfuse, σfuse2)
（两个高斯分布的乘积还是高斯分布）。其中，
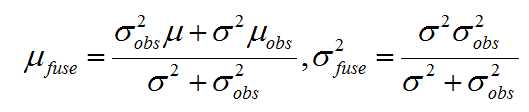
这里的μobs，σobs2该如何才能得到呢？
这里的μobs实际上就是每次我们新三角化出来的深度值，而对于σobs2，就是上面提到的 δp（不确定度σobs）。
那么原始的分布μ，σ2该如何得到呢？
这个很简单，第一次三角化出来的μ，σ2就可以作为初始值，然后每次新三角化出一个三维点，就去更新深度值的分布。
至此，我们似乎得到了一个不错的结果：既简单又优美的公式。
实际上还会存在什么问题呢？
（1）实际的深度值分布是否真的符合高斯分布？
（2）如果我们中间过程有一次三角化的过程求错了，并且还进行了信息融合，会有什么后果？
（3）我们如何避免第二个问题中所提出的情况？
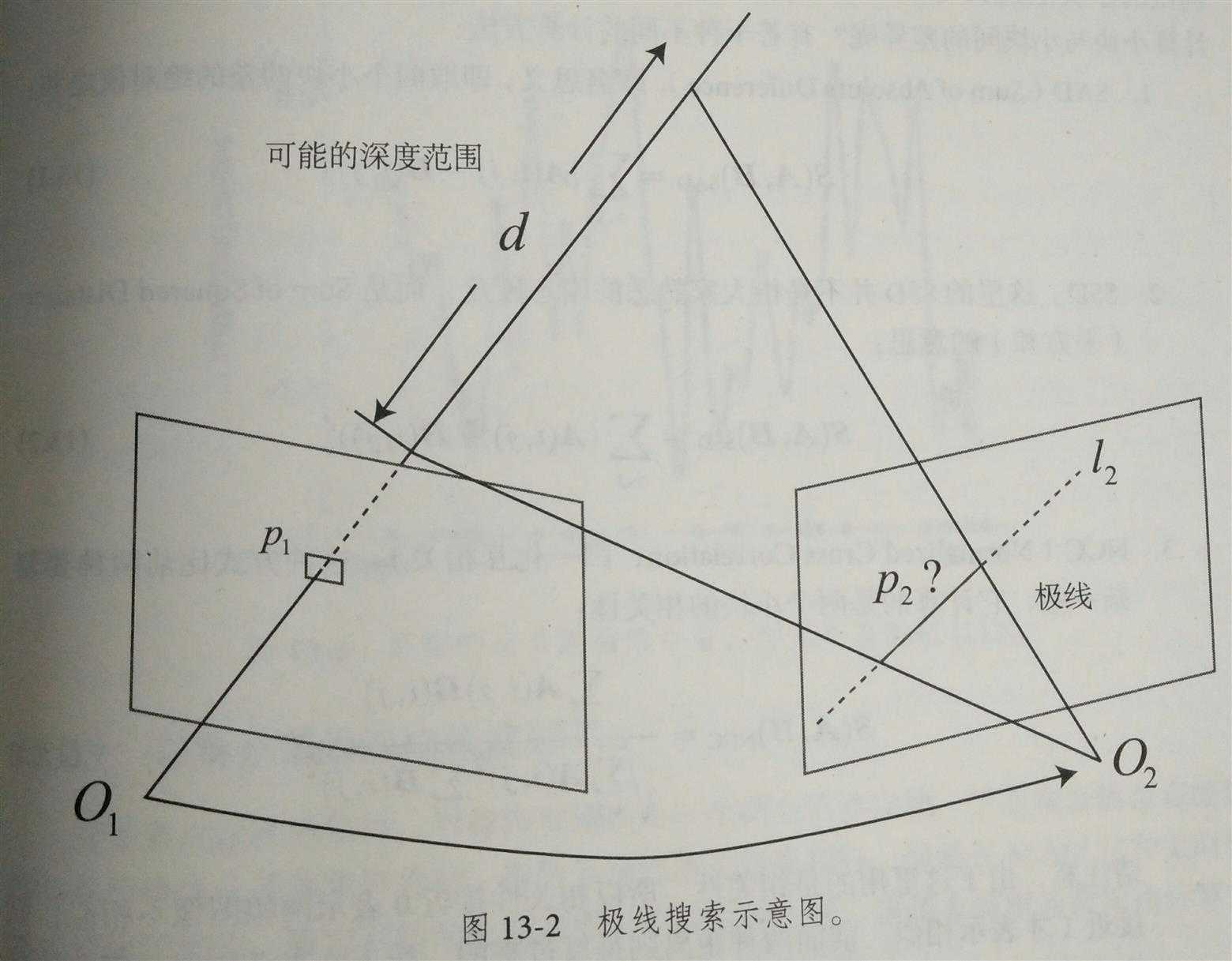
左边的相机观测到了某个像素
，由于是个单目相机，我们无法知道其深度，所以假设深度可能在某个区域内，不妨说是某个最小值到无穷
，即该像素对应的空间点对应在本图中的d射线。在右相机，这条线段的投影也形成图像平面上的一条线，也就是我们称的极线。问题：极线上的哪一点才是我们对应的点呢？
在特征点中，我们通过特征匹配找到了
的位置，然而现在我们没有描述子，所以在极线上搜索与长的相似的点，我们可能沿着右图中的极线从一头走到另一头，逐个比较每个像素与的相似程度。从直接比较像素的角度来看，和直接法是异曲同工的。但在直接法中，我们发现比较单个像素点的亮度并不是稳定可靠的，万一极线上有很多与相似的点，我们如何确定哪一个是真实的呢？所以，既然单个像素的亮度没有区分性，我们来比较像素块，在周围取一个w*w的像小块，然后在极线上也取很多同样大小的小块进行比较，在一定程度上提高区分性，这就是块匹配。
我们把周围的小块记成
，在极线上的n个小块 
。小块与小块之间的差异，用NNC（归一化互相关）来计算，计算的是两小块之间的相关性：
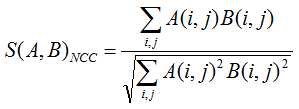
相关性0，表示图像不相似；相关性1，表示图像相似；
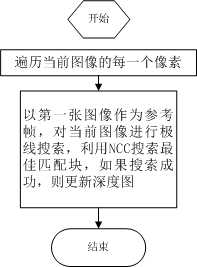
主函数： update：
1 bool update(const Mat& ref, const Mat& curr, const SE3& T_C_R, Mat& depth, Mat& depth_cov )
2 {
3 #pragma omp parallel for
4 for ( int x=boarder; x<width-boarder; x++ )
5 #pragma omp parallel for
6 for ( int y=boarder; y<height-boarder; y++ )
7 {
8 // 遍历每个像素
9 if ( depth_cov.ptr<double>(y)[x] < min_cov || depth_cov.ptr<double>(y)[x] > max_cov ) // 深度已收敛或发散
10 continue;
11 // 在极线上搜索 (x,y) 的匹配
12 Vector2d pt_curr;
13 bool ret = epipolarSearch (
14 ref,
15 curr,
16 T_C_R,
17 Vector2d(x,y),
18 depth.ptr<double>(y)[x],
19 sqrt(depth_cov.ptr<double>(y)[x]),
20 pt_curr
21 );
22
23 if ( ret == false ) // 匹配失败
24 continue;
25
26 // 取消该注释以显示匹配
27 // showEpipolarMatch( ref, curr, Vector2d(x,y), pt_curr );
28
29 // 匹配成功，更新深度图
30 updateDepthFilter( Vector2d(x,y), pt_curr, T_C_R, depth, depth_cov );
31 }
32 }
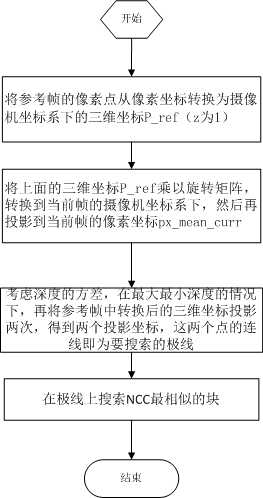
极线搜索：
1 // 极线搜索
2 // 方法见书 13.2 13.3 两节
3 bool epipolarSearch(
4 const Mat& ref, const Mat& curr,
5 const SE3& T_C_R, const Vector2d& pt_ref,
6 const double& depth_mu, const double& depth_cov,
7 Vector2d& pt_curr )
8 {
9 Vector3d f_ref = px2cam( pt_ref );
10 f_ref.normalize();
11 Vector3d P_ref = f_ref*depth_mu; // 参考帧的 P 向量
12
13 Vector2d px_mean_curr = cam2px( T_C_R*P_ref ); // 按深度均值投影的像素
14 double d_min = depth_mu-3*depth_cov, d_max = depth_mu+3*depth_cov;
15 if ( d_min<0.1 ) d_min = 0.1;
16 Vector2d px_min_curr = cam2px( T_C_R*(f_ref*d_min) ); // 按最小深度投影的像素
17 Vector2d px_max_curr = cam2px( T_C_R*(f_ref*d_max) ); // 按最大深度投影的像素
18
19 Vector2d epipolar_line = px_max_curr - px_min_curr; // 极线（线段形式）
20 Vector2d epipolar_direction = epipolar_line; // 极线方向
21 epipolar_direction.normalize();
22 double half_length = 0.5*epipolar_line.norm(); // 极线线段的半长度
23 if ( half_length>100 ) half_length = 100; // 我们不希望搜索太多东西
24
25 // 取消此句注释以显示极线（线段）
26 // showEpipolarLine( ref, curr, pt_ref, px_min_curr, px_max_curr );
27
28 // 在极线上搜索，以深度均值点为中心，左右各取半长度
29 double best_ncc = -1.0;
30 Vector2d best_px_curr;
31 for ( double l=-half_length; l<=half_length; l+=0.7 ) // l+=sqrt(2)
32 {
33 Vector2d px_curr = px_mean_curr + l*epipolar_direction; // 待匹配点
34 if ( !inside(px_curr) )
35 continue;
36 // 计算待匹配点与参考帧的 NCC
37 double ncc = NCC( ref, curr, pt_ref, px_curr );
38 if ( ncc>best_ncc )
39 {
40 best_ncc = ncc;
41 best_px_curr = px_curr;
42 }
43 }
44 if ( best_ncc < 0.85f ) // 只相信 NCC 很高的匹配
45 return false;
46 pt_curr = best_px_curr;
47 return true;
48 }
深度滤波器：
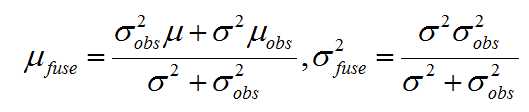
bool updateDepthFilter(
const Vector2d& pt_ref,
const Vector2d& pt_curr,
const SE3& T_C_R,
Mat& depth,
Mat& depth_cov
)
{
// 用三角化计算深度
SE3 T_R_C = T_C_R.inverse();
Vector3d f_ref = px2cam( pt_ref );
f_ref.normalize();
Vector3d f_curr = px2cam( pt_curr );
f_curr.normalize();
// 方程
// d_ref * f_ref = d_cur * ( R_RC * f_cur ) + t_RC
// => [ f_ref^T f_ref, -f_ref^T f_cur ] [d_ref] = [f_ref^T t]
// [ f_cur^T f_ref, -f_cur^T f_cur ] [d_cur] = [f_cur^T t]
// 二阶方程用克莱默法则求解并解之
Vector3d t = T_R_C.translation();
Vector3d f2 = T_R_C.rotation_matrix() * f_curr;
Vector2d b = Vector2d ( t.dot ( f_ref ), t.dot ( f2 ) );
double A[4];
A[0] = f_ref.dot ( f_ref );
A[2] = f_ref.dot ( f2 );
A[1] = -A[2];
A[3] = - f2.dot ( f2 );
double d = A[0]*A[3]-A[1]*A[2];
Vector2d lambdavec =
Vector2d ( A[3] * b ( 0,0 ) - A[1] * b ( 1,0 ),
-A[2] * b ( 0,0 ) + A[0] * b ( 1,0 )) /d;
Vector3d xm = lambdavec ( 0,0 ) * f_ref;
Vector3d xn = t + lambdavec ( 1,0 ) * f2;
Vector3d d_esti = ( xm+xn ) / 2.0; // 三角化算得的深度向量
double depth_estimation = d_esti.norm(); // 深度值
// 计算不确定性（以一个像素为误差）
Vector3d p = f_ref*depth_estimation;
Vector3d a = p - t;
double t_norm = t.norm();
double a_norm = a.norm();
double alpha = acos( f_ref.dot(t)/t_norm );
double beta = acos( -a.dot(t)/(a_norm*t_norm));
double beta_prime = beta + atan(1/fx);
double gamma = M_PI - alpha - beta_prime;
double p_prime = t_norm * sin(beta_prime) / sin(gamma);
double d_cov = p_prime - depth_estimation;
double d_cov2 = d_cov*d_cov;
// 高斯融合
double mu = depth.ptr<double>( int(pt_ref(1,0)) )[ int(pt_ref(0,0)) ];
double sigma2 = depth_cov.ptr<double>( int(pt_ref(1,0)) )[ int(pt_ref(0,0)) ];
double mu_fuse = (d_cov2*mu+sigma2*depth_estimation) / ( sigma2+d_cov2);
double sigma_fuse2 = ( sigma2 * d_cov2 ) / ( sigma2 + d_cov2 );
depth.ptr<double>( int(pt_ref(1,0)) )[ int(pt_ref(0,0)) ] = mu_fuse;
depth_cov.ptr<double>( int(pt_ref(1,0)) )[ int(pt_ref(0,0)) ] = sigma_fuse2;
return true;
}
相信有了上面的流程图，加上前面几章的理论铺垫，你能够比较轻松地看懂这些代码了。祝你阅读代码愉快！
标签：注释 poi tool ati 自然界 消元 3.2 双线性插值 取消
原文地址：http://www.cnblogs.com/Jessica-jie/p/7730731.html
