- 时空限制1s / 512MB
题目描述
组合数C_n^mCnm?表示的是从n个物品中选出m个物品的方案数。举个例子,从(1,2,3) 三个物品中选择两个物品可以有(1,2),(1,3),(2,3)这三种选择方法。根据组合数的定 义,我们可以给出计算组合数的一般公式:
C_n^m=\frac{n!}{m!(n - m)!}Cnm?=m!(n−m)!n!?
其中n! = 1 × 2 × · · · × n
小葱想知道如果给定n,m和k,对于所有的0 <= i <= n,0 <= j <= min(i,m)有多少对 (i,j)满足C_i^jCij?是k的倍数。
输入输出格式
输入格式:
第一行有两个整数t,k,其中t代表该测试点总共有多少组测试数据,k的意义见 【问题描述】。
接下来t行每行两个整数n,m,其中n,m的意义见【问题描述】。
输出格式:
t行,每行一个整数代表答案。
输入输出样例
说明
【样例1说明】
在所有可能的情况中,只有C_2^1 = 2C21?=2是2的倍数。
【子任务】

--------------------------------------------------------------------------------------------------------------------------
写这道题之前,首先要知道二项式定理、杨辉三角、组合数公式以及它们之间的关系
题目给你组合数公式,难不成直接计算?不存在的。看数据范围就知道了
就是利用杨辉三角及二项式定理求组合数的过程
得出的递推式为:
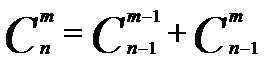
详细见代码:

1 #include<stdio.h> 2 #include<iostream> 3 #define maxn 2010 4 using namespace std; 5 int t,k,n,m,s[maxn][maxn],ans,f[maxn][maxn]; 6 int main(){ 7 scanf("%d %d",&t,&k); 8 for(int i=0;i<maxn;i++) s[i][0]=s[i][i]=1;//边界值,把杨辉三角写出来就知道了 9 for(int i=1;i<maxn;i++) 10 for(int j=1;j<maxn;j++) 11 if(i>=j){ 12 s[i][j]=(s[i-1][j-1]+s[i-1][j])%k;//算出来的值可能很大,所以需要在这里取摸 13 f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1];//f[i][j]即子问题的解,这里是二维前缀和 14 if(!s[i][j]) f[i][j]++; 15 } 16 else f[i][j]=f[i][i]; 17 for(int i=1;i<=t;i++){ 18 scanf("%d %d",&n,&m); 19 printf("%d\n",f[n][m]); 20 } 21 return 0; 22 }

